GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

In order to access this I need to be confident with:

Algebraic terms Simplifying algebraic expressions Collecting like terms Laws of indices Expanding brackets Factorising Simplifying fractions Simplifying algebraic fractions Multiplying and dividing fractions Difference of two squares

This topic is relevant for:

GCSE Maths Algebra Algebraic Expressions Simplifying Expressions Algebraic Fractions

Multiplying Algebraic Fractions

Multiplying And Dividing Algebraic Fractions

Here we will learn about multiplying and dividing algebraic fractions, including algebraic fractions with monomial and binomial numerators and denominators.

There are also multiplying and dividing algebraic fractions worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is multiplying and dividing algebraic fractions?

Multiplying and dividing algebraic fractions is the skill of multiplying and dividing two or more fractions that contain algebraic terms.

For example, $\cfrac{2a}{5}, \cfrac{3-gh}{4f},$ or $\cfrac{1}{x-x^{2}} \, .$

To do this we must combine our knowledge of multiplying and dividing fractions with our understanding of algebra.

Step-by-step guide: Multiplying and dividing fractions

Step-by-step guide: Algebraic terms

What is multiplying and dividing algebraic fractions?

$What is multiplying and dividing algebraic fractions?$

Multiplication with algebraic fractions

To multiply with fractions, we multiply the numerators together, and multiply the denominators together. This is the same for algebraic fractions, but we need to take extra care when multiplying algebraic terms or expressions.

For example, $\cfrac{3x^3}{a} \times \cfrac{5x}{2b}=\cfrac{3x^3\times 5x}{a\times 2b}=\cfrac{15x^4}{2ab} \, .$

Division with algebraic fractions

To divide with fractions, we first write the reciprocal of the dividing fraction and then multiply the numerators together, and multiply the denominators together. This is the same for algebraic fractions, but we need to take extra care when multiplying algebraic terms or expressions.

For example, $\cfrac{4b}{3} \div \cfrac{7a}{b}=\cfrac{4b}{3} \times \cfrac{b}{7a}=\cfrac{4b\times b}{3\times 7a}=\cfrac{4b^2}{21a} \, .$

How to multiply algebraic fractions

In order to multiply algebraic fractions:

Multiply the numerators together and multiply the denominators together.
Simplify the fraction if possible.

Explain how to multiply algebraic fractions

$Explain how to multiply algebraic fractions$

$Algebraic fractions worksheet (includes multiplying algebraic fractions)$

Algebraic fractions worksheet (includes multiplying algebraic fractions)

$Algebraic fractions worksheet (includes multiplying algebraic fractions)$

Get your free multiplying algebraic fractions worksheet of 20+ algebraic fractions questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

$Algebraic fractions worksheet (includes multiplying algebraic fractions)$

Algebraic fractions worksheet (includes multiplying algebraic fractions)

$Algebraic fractions worksheet (includes multiplying algebraic fractions)$

Get your free multiplying algebraic fractions worksheet of 20+ algebraic fractions questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Multiplying algebraic fractions examples

Example 1: multiplying algebraic fractions with monomial expressions.

Write as a single fraction in its simplest form, $\cfrac{2}{a}\times\cfrac{5}{b} \, .$

Multiply the numerators together and multiply the denominators together.

$\cfrac{2\times5}{a\times b}=\cfrac{10}{ab}$

2Simplify the fraction if possible.

The fraction $\cfrac{10}{ab}$ cannot be simplified as the numerator and the denominator do not have any common factors.

The final answer is $\cfrac{10}{ab}.$

Example 2: multiplying algebraic fractions involving a binomial expression

Write as a single fraction in its simplest form, $\cfrac{4x}{5}\times\cfrac{x+7}{8} \, .$

Multiply the numerators together and multiply the denominators together.

$\cfrac{4x\times(x+7)}{5\times8}=\cfrac{4x(x+7)}{40}$

Note that you can leave algebraic products in factorised form. However, to help with step $2$ it is best to check that they are fully factorised.

The terms in the bracket here do not share a common factor other than $1,$ and therefore the expression is fully factorised.

Simplify the fraction if possible.

$\cfrac{4x(x+7)}{40}$

The numerator and the denominator have a common factor of $4$ so we divide both the numerator and the denominator by $4$ to simplify the fraction.

$\cfrac{4x(x+7)\div4}{40\div4}=\cfrac{x(x+7)}{10}$

The final answer is $\cfrac{x(x+7)}{10}.$

If you expand the brackets then another way of writing the final answer is $\cfrac{x^2+7x}{10}.$

Example 3: multiplying algebraic fractions involving binomial expressions

Write as a single fraction in its simplest form, $\cfrac{3x+9}{4x}\times\cfrac{5}{2x+6} \, .$

Multiply the numerators together and multiply the denominators together.

$\cfrac{(3x+9)\times5}{4x\times(2x+6)}=\cfrac{5(3x+9)}{4x(2x+6)}$

Note that you can leave algebraic products in factorised form. However, to help with step $2$ it is best to check that they are fully factorised.

In this case the terms in the brackets of the numerator both have a factor of $3,$ and the terms in the brackets of the denominator both have a factor of $2.$ Therefore we can write the fraction like this.

$\cfrac{5(3x+9)}{4x(2x+6)}=\cfrac{5\times3(x+3)}{4x\times2(x+3)}=\cfrac{15(x+3)}{8x(x+3)}$

Simplify the fraction if possible.

$\cfrac{15(x+3)}{8x(x+3)}$

We can simplify this fraction as the numerator and the denominator share the binomial factor $(x+3).$

$\cfrac{15\cancel{(x+3)}}{8x\cancel{(x+3)}}=\cfrac{15}{8x}$

The final answer is $\cfrac{15}{8x}.$

How to divide algebraic fractions

In order to divide algebraic fractions:

Find the reciprocal of the dividing fraction and rewrite the question with multiplication instead of division.
Multiply the numerators together and multiply the denominators together.
Simplify the fraction if possible.

Expain how to divide algebraic fractions

$Expain how to divide algebraic fractions$

Dividing algebraic fractions examples

Example 4: dividing with algebraic fractions with monomial expressions

Write as a single fraction in its simplest form, $\cfrac{10}{3c}\div\cfrac{5}{3d} \, .$

Find the reciprocal of the dividing fraction and rewrite the question with multiplication instead of division.

$\cfrac{10}{3c}\div\cfrac{5}{3d}=\cfrac{10}{3c}\times\cfrac{3d}{5}$

Multiply the numerators together and multiply the denominators together.

$\cfrac{10}{3c}\times\cfrac{3d}{5}=\cfrac{10\times 3d}{3c\times5}=\cfrac{30d}{15c}$

Simplify the fraction if possible.

$\cfrac{30d}{15c}$

Both the numerator and the denominator have a common factor of $15$ so we divide both the numerator and the denominator by $15$ to simplify the fraction.

$\cfrac{30d\div15}{15c\div15}=\cfrac{2d}{c}$

The final answer is $\cfrac{2d}{c}.$

Example 5: dividing with algebraic fractions involving a binomial expression

Write as a single fraction in its simplest form, $\cfrac{3x}{4}\div\cfrac{x+1}{8} \, .$

Find the reciprocal of the dividing fraction and rewrite the question with multiplication instead of division.

$\cfrac{3x}{4}\div\cfrac{x+1}{8}=\cfrac{3x}{4}\times\cfrac{8}{x+1}$

Multiply the numerators together and multiply the denominators together.

$\cfrac{3x}{4}\times\cfrac{8}{x+1}=\cfrac{3x\times 8}{4\times(x+1)}=\cfrac{24x}{4(x+1)}$

Note that you can leave algebraic products in factorised form. However, to help with step $2$ it is best to check that they are fully factorised.

The terms in the bracket here do not share a common factor other than $1,$ and therefore the expression is fully factorised.

Simplify the fraction if possible.

$\cfrac{24x}{4(x+1)}$

Both the numerator and the denominator have a common factor of $4$ so we divide both the numerator and the denominator by $4$ to simplify the fraction.

$\cfrac{24x}{4(x+1)}=\cfrac{24x\div4}{4(x+1)\div4}=\cfrac{6x}{x+1}$

The final answer is $\cfrac{6x}{x+1}.$

Example 6: dividing with algebraic fractions with binomial expressions

Write as a single fraction in its simplest form, $\cfrac{x^{2}-9}{x+1}\div\cfrac{x+3}{2} \, .$

Find the reciprocal of the dividing fraction and rewrite the question with multiplication instead of division.

$\cfrac{x^{2}-9}{x+1}\div\cfrac{x+3}{2}=\cfrac{x^{2}-9}{x+1}\times\cfrac{2}{x+3}$

Multiply the numerators together and multiply the denominators together.

$\cfrac{x^{2}-9}{x+1}\times\cfrac{2}{x+3}=\cfrac{(x^{2}-9)\times2}{(x+1)\times(x+3)}=\cfrac{2(x^{2}-9)}{(x+1)(x+3)}$

Note that you can leave algebraic products in factorised form. However, to help with step $2$ it is best to check that they are fully factorised.

The bracket of the numerator is the difference of two squares and can be factorised into double brackets.

$\cfrac{2(x^{2}-9)}{(x+1)(x+3)}=\cfrac{2(x-3)(x+3)}{(x+1)(x+3)}$

Simplify the fraction if possible.

$\cfrac{2(x+3)(x-3)}{(x+1)(x+3)}$

We can now cancel a common binomial factor of $(x+3).$

$\cfrac{2\cancel{(x+3)}(x-3)}{(x+1)\cancel{(x+3)}}=\cfrac{2(x-3)}{x+1}$

The final answer is $\cfrac{2(x-3)}{x+1}.$

Step-by-step guide: Difference of two squares

Common misconceptions

Cross multiplying vs multiplying fractions
When multiplying fractions, we multiply the numerators together, and multiply the denominators together. Some students can confuse this with a method referred to as ‘cross multiplying’ which some people teach as a method for dividing by a fraction.

For example,
Incorrectly choosing to cross multiply,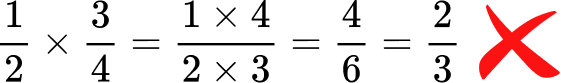

The correct solution is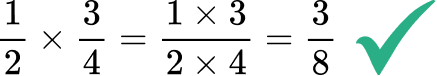

Common denominators are not needed
When we add or subtract fractions we must ensure there is a common denominator. A mistake often made by students is to believe this rule also applies to the multiplication of fractions. When we are multiplying fractions, we can choose to write the fractions with a common denominator but this simply makes the process lengthier and it is not necessary.

For example,
Without writing the fractions with a common denominator,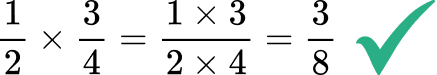

Writing the fractions with a common denominator first,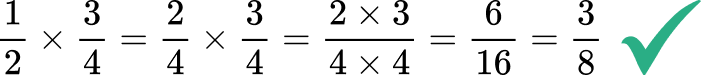

Practice multiplying and dividing algebraic fractions questions

\cfrac{3f}{16e}

\cfrac{16e}{3f}

\cfrac{24}{2ef}

\cfrac{12}{ef}

$\cfrac{3}{2e}\times\cfrac{8}{f}=\cfrac{3\times{8}}{2e\times{f}}=\cfrac{24}{2ef}=\cfrac{12}{ef}$

\cfrac{6x+9}{4(2x+1)}

\cfrac{4x^{2}+8x+3}{3}

\cfrac{14x+13}{6}

\cfrac{4x^{2}+8x+3}{6}

$\cfrac{2x+3}{2}\times\cfrac{2(2x+1)}{3}=\cfrac{(2x+3)\times{(2(2x+1))}}{6}=\cfrac{8x^{2}+16x+6}{6}=\cfrac{4x^{2}+8x+3}{3}$

\cfrac{8(x+1)^{2}}{21x}

\cfrac{12x^{2}+12}{14x+4}

\cfrac{6x}{7}

\cfrac{12x^{2}}{14}

$\cfrac{4x+4}{7}\times\cfrac{3x}{2x+2}=\cfrac{(4x+4)\times{3x}}{7\times(2x+2)}=\cfrac{3x\times{4(x+1)}}{7\times2(x+1)}=\cfrac{12x(x+1)}{14(x+1)}=\cfrac{6x}{7}$

\cfrac{5}{2x^{3}}

\cfrac{13}{x}

\cfrac{5}{2x}

\cfrac{5}{2x^{2}}

$\cfrac{15}{4x^{2}}\div\cfrac{3x}{2}=\cfrac{15}{4x^{2}}\times\cfrac{2}{3x}=\cfrac{30}{12x^{3}}=\cfrac{5}{2x^{3}}$

\cfrac{1+x}{12-x^{2}}

\cfrac{20+x}{12x^{2}}

\cfrac{5+x}{3x^{2}}

\cfrac{5}{3x}

$\cfrac{5+x}{12}\div\cfrac{x^{2}}{4}=\cfrac{5+x}{12}\times\cfrac{4}{x^{2}}=\cfrac{4(5+x)}{12x^{2}}=\cfrac{5+x}{3x^{2}}$

\cfrac{x^{2}-72}{4(x-2)(x-6)}

\cfrac{x-18}{2}

\cfrac{x+6}{2(x-2)}

\cfrac{6-x}{2x}

$\cfrac{x^{2}-36}{4x-8}\div\cfrac{x-6}{2}=\cfrac{x^{2}-36}{4x-8}\times\cfrac{2}{x-6}=\cfrac{(x^{2}-36)\times{2}}{(4x-8)\times(x-6)}=\cfrac{2(x+6)(x-6)}{4(x-2)(x-6)}$

$=\cfrac{2(x+6)}{4(x-2)}=\cfrac{x+6}{2(x-2)}$

Multiplying and dividing algebraic fractions GCSE questions

1. Write as a single fraction, $\cfrac{2}{x}\times\cfrac{3}{y}\div\cfrac{5}{z}.$

(3 marks)

Show answer

$\cfrac{6}{xy}\div\cfrac{5}{z}$

(1)

$\cfrac{6}{xy}\times\cfrac{z}{5}$

(1)

$\cfrac{6z}{5xy}$

(1)

2. Triangle $ABC$ is a right angled triangle where $BC$ is perpendicular to $AC$ and $x > 0.$

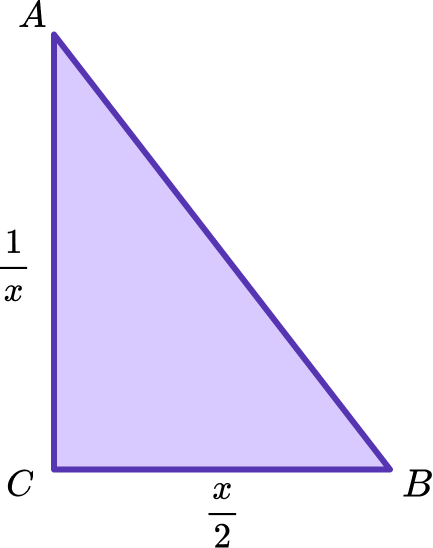
Multiplying And Dividing Algebraic Fractions GCSE question 2

(a) Calculate the area of the triangle.

(b) As the value of $x$ increases, what happens to the area of the triangle?

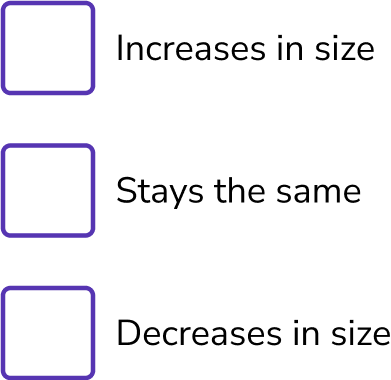
Multiplying And Dividing Algebraic Fractions GCSE question 2b

Explain your answer.

(4 marks)

Show answer

(a) $(\cfrac{1}{x}\times\cfrac{x}{2})\div{2}$

(1)

$\cfrac{x}{2x}(=\cfrac{1}{2})\div{2}$

$\cfrac{1}{2}\times\cfrac{1}{2}$

(1)

$\cfrac{1}{4}$

(1)

(b) Stays the same.

The area is independent of the value of $x.$

(1)

3. Use factorisation to fully simplify $\cfrac{4x^{2}-16}{x+1}\div\cfrac{x-2}{3x+3}$ into the form $a(x+b)$ where $a$ and $b$ are integers.

(5 marks)

Show answer

$4x^{2}-16=4(x^{2}-4)$

(1)

$4(x^{2}-4)=4(x+2)(x-2)$

(1)

$3x+3=3(x+1)$

(1)

$\cfrac{4(x+2)(x-2)}{x+1}\div\cfrac{x-2}{3(x+1)}=\cfrac{4(x+2)(x-2)}{x+1}\times\cfrac{3(x+1)}{x-2}$

(1)

$\cfrac{4(x+2)(x-2)\times{3}(x+1)}{(x+1)(x-2)}=12(x+2)$

(1)

Learning checklist

You have now learned how to:

Multiply and divide with algebraic fractions

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.