Surface area of a pyramid

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

Faces, edges and vertices Substitution Area of a triangle Area of quadrilaterals Pythagoras’ theorem

This topic is relevant for:

GCSE Maths Geometry and Measure 3D Shapes Pyramid

Surface Area Of A Pyramid

Here we will learn about the surface area of a pyramid, including how to find the area of the base and the triangular faces of a pyramid and how to structure a logical solution to calculate the surface area of a pyramid.

There are also surface area of a pyramid worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the surface area of a pyramid?

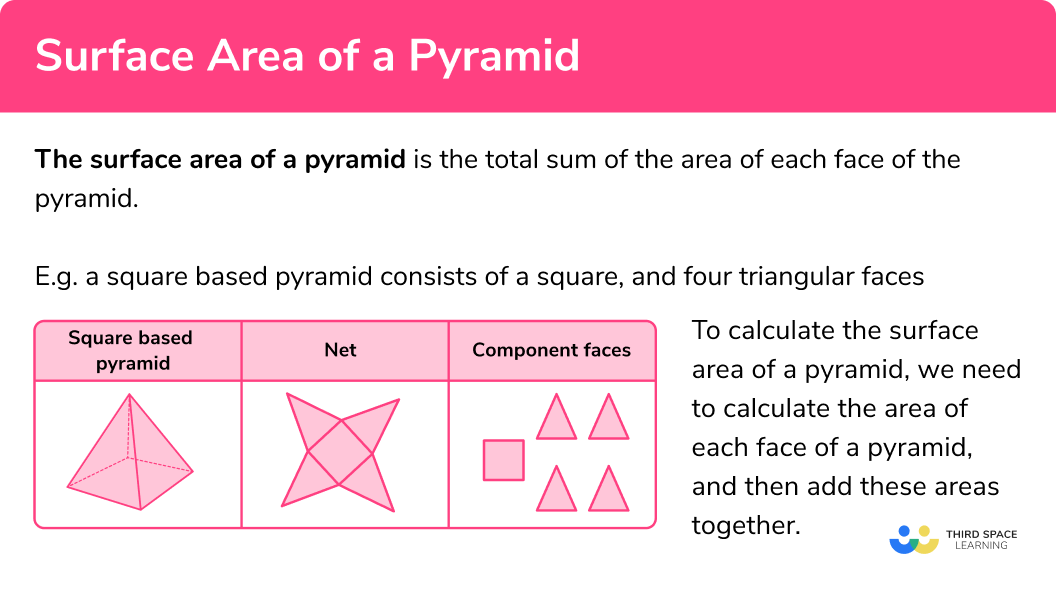
The surface area of a pyramid is the total sum of the area of each face of the pyramid.

For example, a square based pyramid consists of a square, and four triangular faces.

Note:

There are many types of pyramids

A rectangular based pyramid consists of a rectangle and two pairs of identical triangles
A triangular based pyramid consists of $4$ triangular faces.
The base could be any regular polygon or irregular polygon e.g pentagonal or hexagonal pyramids. You need to make sure you have found the area of all lateral faces and added it to the area of the base of the pyramid.

To calculate the total surface area of a pyramid, we need to calculate the area of each face of a pyramid, and then add these areas together. This is exactly the same approach if we were calculating the area of a compound shape.

E.g. Work out the surface area of the pyramid.

$\begin{aligned} &\text{Area of the base }=5\times{5}=25\text{ cm}^{2} \\\\ &\text{Area of a triangular face }=\frac{1}{2}\times{8}\times{5}=20\text{ cm}^{2} \\\\ &\text{Surface area }=25+20+20+20+20=25+(4\times{20})=105\text{ cm}^{2} \end{aligned}$ .

As one single calculation, we can say:

\begin{aligned} \text{Surface area of pyramid}&= \text{Area of base} + \text{Area of triangular faces}\\\\ &=5^2+4\times (\frac{1}{2}\times 5 \times 8)\\\\ &=25+80\\\\ &=105 \ cm^2 \end{aligned}

What is the surface area of a pyramid?

Key parts of a pyramid

Visualising the individual faces of a pyramid is a key skill.

The apex is the convergent point to which all the slanted edges of the pyramid meet.

The apex is located above the base of a pyramid, and the height of the pyramid is the perpendicular distance between the base and the apex.

Let us have a look to see what happens to the triangular faces when we move the apex for a square based pyramid.

*For each pyramid, the base is a congruent square.

Note: It is likely that a pyramid will be regular, nevertheless, you may still have to find the surface area of an oblique pyramid (see example $6$ below). If you follow the steps carefully, you should be able to find the surface area of any pyramid.

How to find the surface area of a pyramid

In order to find the surface area of a pyramid:

Calculate the area of the base.
Calculate the area of all of the triangular faces.
Calculate the total surface area.
Write the answer, including the units.

How to find the surface area of a pyramid

Volume and surface area of pyramids worksheet

Get your free surface area of a pyramid worksheet of 20+ volume and surface area of pyramids questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Volume and surface area of pyramids worksheet

Get your free surface area of a pyramid worksheet of 20+ volume and surface area of pyramids questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Surface area of a pyramid examples

Example 1: square-based pyramid in cm

The apex of a square-based pyramid is directly above the centre of the base. Using the diagram below, calculate the surface area of the pyramid.

Calculate the area of the base.

The base is a square with the area $6\times{6}=6^{2}=36\text{ cm}^2$ .

2Calculate the area of all of the triangular faces.

As the apex of the pyramid is directly above the centre of the base, all four triangular faces are identical and so we can calculate the area of one of these triangles, and multiply the solution by $4$ .

The area of a triangle is calculated using the formula $A=\frac{1}{2}bh$ where $b$ is the base of the triangle, and $h$ is the vertical height of the triangle. We therefore have the area of each triangle to be:

\begin{aligned} A&=\frac{1}{2}\times{b}\times{h}\\\\ &=\frac{1}{2}\times{10}\times{6}\\\\ &=30\text{ cm}^{2} \end{aligned}

4A=30\times{4}=120\text{ cm}^{2}.

3Calculate the total surface area.

Adding the values for the area of the base and the area of the four triangles, we get:

SA=36+120=156

4Write the answer, including the units.

SA=156\text{ cm}^{2}

Example 2: square-based pyramid, worded problem

A softbox light takes the form of a solid, square-based pyramid. The screen has a width of $1m,$ and the sides of the softbox light have a perpendicular height of $1.2m.$

The apex of the pyramid is perpendicular to the centre of the screen.

Calculate the surface area of the softbox light.

Calculate the area of the base.

Here, the screen is the base. As the screen is a square, the area of the square is $1\times{1}=1\text{ m}^{2}$ .

Calculate the area of all of the triangular faces.

As the apex is perpendicular to the centre of the screen, each side of the softbox light is an identical, isosceles triangle.

$\begin{aligned} A&=\frac{1}{2}\times{b}\times{h}\\\\ &=\frac{1}{2}\times{1}\times{1.2}\\\\ &=0.6\text{ m}^{2} \end{aligned}$

$4A=4\times{0.6}=2.4\text{ m}^2$

Calculate the total surface area.

SA=1+2.4=3.4

Write the answer, including the units.

SA=3.4\text{ m}^{2}

Example 3: triangular-based pyramid

A regular tetrahedron is a special type of triangular-based pyramid as all faces of a regular tetrahedron are congruent, equilateral triangles. Using the diagram below, calculate the surface area of the regular tetrahedron.

Calculate the area of the base.

As each face of the tetrahedron is the same equilateral triangle, the area of the triangular base is the same as the area of each of the other triangular faces.

$\begin{aligned} A&=\frac{1}{2}\times{b}\times{h}\\\\ &=\frac{1}{2}\times{8}\times{4\sqrt{3}}\\\\ &=16\sqrt{3} \end{aligned}$

Calculate the area of all of the triangular faces.

Again the area of each face is the same and so the area of the other three triangular faces is also equal to $16\sqrt{3}$ .

Calculate the total surface area.

Adding the area of each face together, we get:

$SA=16\sqrt{3}+16\sqrt{3}+16\sqrt{3}+16\sqrt{3}=4\times{16}\sqrt{3}=64\sqrt{3}$

Write the answer, including the units.

SA=64\sqrt{3}\text{ cm}^{2}

Example 4: rectangular-based pyramid

$ABCDE$ is a rectangular-based pyramid. The vertex $E$ is directly above the centre of the base $ABCD$ . Calculate the surface area of the pyramid. Write your answer in square centimetres.

Calculate the area of the base.

The units for the base are not the same, so we need to make sure that they are for the calculations to be accurate. As the question asks for the answer to be written in square centimetres, we need to convert the units to centimetres first.

$1.2m=120cm.$

The area of the base is therefore:

$A=120\times{90}=10800\text{ cm}^2$

Calculate the area of all of the triangular faces.

The pyramid has two pairs of congruent faces: $ADE=BCE$ and $CDE=ABE.$

Calculating the area of $ADE$ , we have

$A=\frac{1}{2}\times{120}\times{380}=22800\text{ cm}^2$

Triangle $ADE=22800\text{ cm}^2$

Triangle $BCE=22800\text{ cm}^2$

Calculating the area of $CDE$ , we have

$A=\frac{1}{2}\times{90}\times{382}=17190\text{ cm}^2$

Triangle $CDE=17190\text{ cm}^2$

Triangle $ABE=17190\text{ cm}^2$

Calculate the total surface area.

Adding all of the areas together, we have:

$\begin{aligned} SA&=10800+22800+22800+17190+17190\\\\ &=10800+2(22800)+2(17190)\\\\ &=90780 \end{aligned}$

Write the answer, including the units.

SA=90780\text{ cm}^2

Example 5: square-based pyramid net

Using the net below, calculate the surface area of the square-based pyramid. Write your answer to $1$ decimal place.

Calculate the area of the base.

The base is a square and so the area of the base is $5.6\times{5.6}=31.36\text{ cm}^2$

Calculate the area of all of the triangular faces.

To calculate the area of a triangle, we need to know the height of the triangle. To do this, we need to use Pythagoras theorem (remember the base of the right angle triangle is half the width of the isosceles triangle in the net):

Surface area of a pyramid Example 5 Step 2

$h=\sqrt{7.8^{2}-2.8^{2}}=\sqrt{53}$

The area of the triangle above is therefore:

$\begin{aligned} A&=\frac{1}{2}\times{5.6}\times{\sqrt{53}} \\\\ A&=20.38430769… \end{aligned}$

The area of all four of these triangles is therefore:

$4A=4\times{20.38430769}=81.53723076\text{ cm}^2$

Calculate the total surface area.

Adding all of the areas together, we have:

$\begin{aligned} SA&=31.36+81.53723076\\\\ &=112.8972308 \end{aligned}$

Write the answer, including the units.

SA=112.9\text{ cm}^2\text{ (1dp)}

Example 6: square-based pyramid, offset apex

Below is the oblique, square-based pyramid $ABCDE.$ The apex $E$ is directly above the vertex $D$ . Given that $AB=8cm , \ BC=4cm, \ DE=6cm, \ CE=10cm,$ and $AE=2\sqrt{13}\text{ cm}$ , calculate the surface area of the square-based pyramid.

Calculate the area of the base.

The base is a rectangle. The area of the rectangle is $8\times{4}=32\text{ cm}^2$

Calculate the area of all of the triangular faces.

Let’s work through each triangular face separately as they are all different sizes.

$\begin{aligned} &ABE=\frac{1}{2}\times{8}\times{2\sqrt{13}}=8\sqrt{13}\text{ cm}^{2} \\\\ &CDE=\frac{1}{2}\times{8}\times{6}=24\text{ cm}^{2} \\\\ &ADE=\frac{1}{2}\times{4}\times{6}=12\text{ cm}^{2} \end{aligned}$

$BCE=\frac{1}{2}\times{4}\times{10}=20\text{ cm}^2$

Calculate the total surface area.

Adding up all of the values for each face of the square-based pyramid, we have the surface area to be:

$SA=32+8\sqrt{13}+24+12+20=116.8444102…$

Write the answer, including the units.

SA=116.8\text{ cm}^2

Common misconceptions

The height of the triangle is the perpendicular height

The height of the triangle needs to be the perpendicular height. Then we can use the perpendicular height of the triangle to find its area.

Surface area has square units

The surface area will have square units such as square centimetres ( $cm^2$ ) or square metres ( $m^2$ ).

Be accurate

When there are two or more steps in your workings, do not round your workings. For example – do not round the area of the triangular faces. Only round at the end of the question so that your answer is accurate.

Take care with rounding

At the end of the question, make sure you round your answer to the correct number of decimal places or significant figures.

Surface area of a pyramid is part of our series of lessons to support revision on pyramids. You may find it helpful to start with the main pyramid lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Practice surface area of a pyramid questions

384 \text{ cm}^2

260 \text{ cm}^2

140 \text{ cm}^2

224 \text{ cm}^2

\begin{aligned} \text{Surface area of pyramid}&= \text{Area of base} + \text{Area of triangular faces}\\\\ &=8^2+4\times (\frac{1}{2}\times 8\times 10)\\\\ &=64+160\\\\ &=224 \ cm^2 \end{aligned}

781 \text{ m}^2

330 \text{ m}^2

451 \text{ m}^2

555 \text{ m}^2

\begin{aligned} \text{Surface area of pyramid}&= \text{Area of base} + \text{Area of triangular faces}\\\\ &=11^2+4\times (\frac{1}{2}\times 11\times 15)\\\\ &=121+330\\\\ &=451 \ m^2 \end{aligned}

7280 \text{ cm}^2

4788 \text{ cm}^2

1366 \text{ cm}^2

3077 \text{ cm}^2

\begin{aligned} \text{Surface area of pyramid}&= \text{Area of base} + \text{Area of triangular faces}\\\\ &=(42\times{10})+2\times (\frac{1}{2}\times{42}\times{52})+2\times (\frac{1}{2}\times{10}\times{47.3})\\\\ &=420+2184+473\\\\ &=3077 \text{ cm}^2 \end{aligned}

27.5 \text{ cm}^2

55.0 \text{ cm}^2

38.8 \text{ cm}^2

25.9 \text{ cm}^2

The pyramid is a square-based pyramid as the width is $1.95 \times 2=3.9cm.$

\begin{aligned} \text{Surface area of pyramid}&= \text{Area of base} + \text{Area of triangular faces}\\\\ &=3.9^2+4\times (\frac{1}{2}\times 3.9\times 5.1)\\\\ &=15.21+39.78\\\\ &=54.99\\\\ &=55.0\text{ cm}^{2}\text{ (1dp)} \end{aligned}

336 \text{ cm}^2

240 \text{ cm}^2

264 \text{ cm}^2

384 \text{ cm}^2

First we need to find the height of the triangular face.

h=\sqrt{10^{2}-6^{2}}=8\text{ cm}

\begin{aligned} \text{Surface area of pyramid}&= \text{Area of base} + \text{Area of triangular faces}\\\\ &=12^2+4\times (\frac{1}{2}\times 12\times 8)\\\\ &=144+192\\\\ &=336 \text{ cm}^2 \end{aligned}

48 \text{ cm}^2

68.8 \text{ cm}^2

112 \text{ cm}^2

64 \text{ cm}^2

The area of the base is $4\times{4}=16\text{ cm}^2$

The area of two of the triangles is:

(\frac{1}{2}\times{6}\times{4})\times{2}=24\text{ cm}^2

The height of the other two triangular faces is (using Pythagoras theorem):

h=\sqrt{4^{2}+6^{2}}=2\sqrt{13}

The area of the other two triangles is now equal to:

(\frac{1}{2}\times{2\sqrt{13}}\times{4})\times{2}=8\sqrt{13}\text{ cm}^2

The total surface area is therefore:

SA=16+24+8\sqrt{13}=68.8\text{ cm}^2\text{ (1dp)}

Surface area of a pyramid GCSE questions

1. The diagram shows a pyramid. The apex is perpendicular to the centre of the square base.

Surface area of a pyramid GCSE Question 1

Calculate the surface area of the pyramid.

(3 marks)

Show answer

\frac{1}{2}\times 9 \times 12=54

(1)

9^2+4\times 54

(1)

297 \ cm^2

(1)

2. The diagram shows a square-based pyramid.

Surface area of a pyramid GCSE Question 2

Calculate the surface area of the pyramid.

Give your answer in $cm^2.$

(4 marks)

Show answer

1.3 \text{ m} = 130 \text{ cm}

(1)

\frac{1}{2}\times 70 \times 130=4550

(1)

70^2+4\times 4550

(1)

23100

(1)

3. Here is the net of a square-based pyramid.

Surface area of a pyramid GCSE Question 3

Calculate the surface area of the pyramid.

Give your answer in $cm^2.$

(4 marks)

Show answer

\sqrt{13^2-5^2}=12

(1)

\frac{1}{2}\times 10 \times 12=60

(1)

10^2+4\times 60

(1)

340

(1)

4. (a) A fair, tetrahedral dice has a side length of $12mm$ . Calculate the perpendicular height of each face of the tetrahedron. Write your answer as a simplified surd.

(b) Use your answer to part (a) to calculate the surface area of the dice. Write your answer in the form $a\sqrt{b}\text{ mm}^{2}$ where $a$ and $b$ are integers to be found.

(4 marks)

Show answer

(a)

\sqrt{12^2-6^2}

(1)

6\sqrt{3}\text{ cm}

(1)

(b)

\frac{1}{2}(12\times{6\sqrt{3}})\times{4}

(1)

144\sqrt{3}\text{ mm}^{2}

(1)

Learning checklist

You have now learned how to:

Calculate surface areas of pyramids

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.