Conversion of units

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

Multiplying fractions Dividing fractions Multiplying decimals Dividing decimals Metric units of measurement

This topic is relevant for:

GCSE Maths Ratio and Proportion Units Of Measurement

Conversion Of Units

Here we will learn about the conversion of units including converting between metric units and imperial units and converting between units of time.

There are also units of measurement worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the conversion of units?

The conversion of units allows unit conversion to take place between metric and imperial units of measurement for units of length, area and volume, and between seconds, minutes and hours.

To do this we need to know how the units of measurement are linked so that we can work out the conversion factor.

The metric system of units of measurement is based on powers of $10.$ Prefixes such as kilo and milli are used to indicate which power of $10$ is involved.

E.g.

1 \ km=1000 \ m

1 \ m= 100 \ cm

1 \ m= 1000 \ mm

1 \ cm= 10 \ mm

The imperial system is an older system of measurements but some are still used in everyday life.

E.g.

$1$ foot $=12$ inches

$3$ feet $=1$ yard

$1760$ yards $=1$ mile

Time uses a sexagesimal system based on the number $60$

There are $\bf{60}$ seconds in $\bf{1}$ minutes.

There are $\bf{60}$ minutes in $\bf{1}$ hour.

The SI (the international system of units) unit for time is the second $(s).$

You are expected to convert between the different systems of measurements including units of time, metric units and to convert between metric and imperial units.

Let’s look at converting between inches (imperial units) and centimetres (metric units).

We can see from this ruler that $1$ inch is approximately equal to $2.5$ centimetres

If we go from inches to centimetres we multiply by the conversion factor.

If we go from centimetres to inches we divide by the conversion factor.

Note: we use the $\ \approx \$ symbol which means “approximately equal to”.

E.g.

Using the information

1 \ inch \approx 2.5 \ cm

Write $14$ inches as $cm$

The conversion factor is $2.5.$

14\times 2.5 = 35

So,

14 \ inch \approx 35 \ cm

Currency conversion

The skills for the conversion of units can also be applied to currency conversion. Different countries use different currencies. How currencies are linked are known as the exchange rate.

E.g.

The exchange rate is: £1 = $1.27

Work out how many American dollars is £200 worth.

We would use the conversion factor 1.27

200\times 1.27=254

So, £200 is worth $254.

What is the conversion of units?

Units of money, distance, time, density, mass, volume and area

When we travel abroad this involves converting currencies into the currency of the country we’re visiting. We use exchange rates to calculate the amounts.

E.g.

Laura went to Spain.

She changes £225 into euros, €.

The exchange rate was $£1 = €1.62$

How many euros did Laura get?

So, $225 \times 1.62 = €364.50$

E.g.

On her return to England, Laura changed €66 into pounds.

The new exchange rate was $£1 = €1.50$ .

How many pounds did Laura get?

So, $66 \div 1.50 = £44$

We can convert units of length and time using conversion factors. The conversion factor is a number we can use to change one set of units to another, by multiplying or dividing. We can convert units of lengths by remembering the most common metric unit conversions:

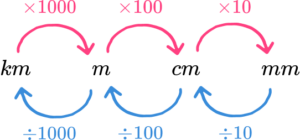
E.g.

Convert 400cm into metres.

There are 100cm in 1m. This is our conversion factor. To convert from cm to m we need to divide.

So, $400 \div 100 = 4m$ .

E.g.

Phoebe runs 500m every day.

Work out how far Phoebe runs in one week.

Give your answer in kilometres.

500m \times 7 = 3500m

3500m \div 1000 = 3.5km

We can convert units of time by remembering the most common unit conversions:

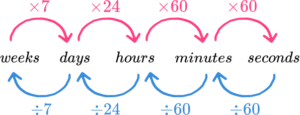
E.g.

How many minutes are there in 5 hours?

There are 60 minutes in 1 hour.

So, $5 /times 60 = 300$ minutes.

Density, mass and volume are proportional.

Volume measures the space inside a three-dimensional object. In ascending order of size, the most common units of volume are $mm^{3}, cm^{3}, m^{3}$ and $km^{3}$ .

E.g.

The volume of water on Earth is 1.386 billion $km^{3}$ .

We can convert between units of volume using the conversion factors below.

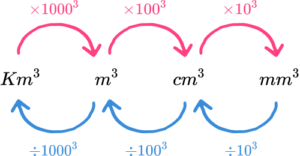
E.g.

Convert $2m^{3}$ into $cm^{3}$

2 /times 100^{3} = 2000000cm^{3}

Mass measures the weight of an object. In ascending order of size, the most common units of mass are grams and kilograms.

E.g.

The total mass of the average car is 1500kg.

The total mass of the average apple is between 70 and 100 grams.

Density is a measure that compares how heavy different materials are. It is a measurement of the amount of a substance contained in a specific volume. The most commonly used units for density are grams per cubic centimetre. We can also express it as kilograms per cubic metre.

E.g.

The density of water is 1 gram per cubic centimetre.

The Earth’s density is 5.51 grams per cubic centimetre.

Area is the amount of surface a two-dimensional shape covers. We measure area in units of length squared. In ascending order of size, the most common units of area are $mm^{2}, cm^{2}$ and $m^{2}$ .

E.g.

The area of a rectangle with length 4m and width 2m is 8 $m^{2}$ .

We can convert between units of area using the conversion factors below.

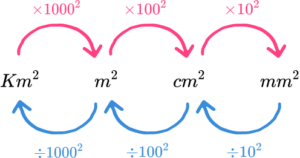
E.g.

Convert $5m^{2}$ into $cm^{2}$

$5 \times 100^{2} = 50000cm^{2}$ .

How to convert of units

In order to convert measurement units:

Find the conversion factor.
Multiply or divide by the conversion factor.
Write down the answer.

How to convert of units

Conversion of units worksheet

Get your free conversion of units worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Conversion of units worksheet

Get your free conversion of units worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on units of measurement

Conversion of units is part of our series of lessons to support revision on units of measurement. You may find it helpful to start with the main units of measurement lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Conversion of units examples

Example 1: converting units of time

Convert $2$ hours to seconds

Find the conversion factor.

1 \ hour \ = 60 \ minutes.

So the conversion factor for hours and minutes is $60$ .

1 \ minute \ = 60 \ seconds

So the conversion factor for minutes and seconds is $60$ .

2Multiply or divide by the conversion factor.

We need to multiply by $60$ to convert from hours to minutes, and then multiply by $60$ again to convert from minutes to seconds.

2 \ hours \ =2 \times 60=120 \ minutes

120 \ minutes \ =120 \times 60=7200 \ seconds

3Write down the answer.

2 \ hours \ =7200 \ seconds

Alternatively, you could have done this in one calculation:

2 \ hours \ =2 \times 60^2 = 7200 \ seconds

Example 2: converting units of time

Convert $3.25$ hours to seconds

Find the conversion factor.

1 \ hour \ = 60 \ minutes.

So the conversion factor for hours and minutes is $60.$

$1 \ minute \ = 60 \ seconds$

So the conversion factor for minutes and seconds is $60.$

Multiply or divide by the conversion factor.

We need to multiply by $60$ to convert from hours to minutes, and then multiply by $60$ again to convert from minutes to seconds.

$3.25 \ hours \ =3.25 \times 60=195 \ minutes$

$195 \ minutes \ =195 \times 60=11 \ 700 \ seconds$

Write down the answer.

3.25 \ hours \ =11 \ 700 \ seconds

Alternatively, you could have done this in one calculation:

$3.25 \ hours \ =3.25 \times 60^2 =11 \ 700 \ seconds$

Example 3: metric/imperial conversion

1 \ foot \approx 30 \ cm

Convert $13 \ feet$ to $cm$ .

Find the conversion factor.

The conversion factor for feet and centimetres is $30$

Multiply or divide by the conversion factor.

As we are converting from $feet$ to $cm$ , we multiply by the conversion factor.

$13 \times 30=390$

Write down the answer.

We can write down the approximated conversion.

$13 \ feet \approx 390 \ cm$

Example 4: metric/imperial conversion

1 \ hectare \approx 2.5 \ acres

Convert $14.8$ acres to hectares.

Find the conversion factor.

The conversion factor for hectares and acres is $2.5$

Multiply or divide by the conversion factor.

As we are converting from acres to hectares, we divide by the conversion factor.

$14.8 \div 2.5=5.92$

Write down the answer.

We can write down the approximated conversion.

$14.8 \ hectare\ \approx 5.92 \ acres$

Example 5: miles/kilometres conversion

5 \ miles \approx 8 \ km

Convert $30 \ miles$ to $km$ .

Find the conversion factor.

We can find the conversion factor by first dividing by $5$ to work out what $1$ mile is equivalent to.

$\begin{aligned} 5\ miles &\approx 8\ km\\\\ 1\ mile &\approx 1.6\ km \end{aligned}$

The conversion factor from miles to kilometres is $1.6$

Multiply or divide by the conversion factor.

As we are converting from $miles$ to $km$ , we multiply by the conversion factor.

$30 \times 1.6=48$

Write down the answer.

We can write down the approximated conversion.

$30\ miles \approx 48 \ km$

Alternatively we could have used a fractional conversion factor of $\frac{8}{5}.$

$30\times \frac{8}{5}=48$

Example 6: miles/kilometres conversion

5 \ miles \approx 8 \ km

Convert $120 \ km$ to $miles$ .

Find the conversion factor.

We can find the conversion factor by first dividing by $5$ to find what $1 \ mile$ is equivalent to.

$\begin{aligned} 5\ miles &\approx 8\ km\\\\ 1\ mile &\approx 1.6\ km \end{aligned}$

The conversion factor from miles to kilometres is $1.6$

Multiply or divide by the conversion factor.

As we are converting from kilometres to miles, we divide by the conversion factor.

$120\div 1.6=75$

Write down the answer.

We can write down the approximated conversion.

$120\ km \approx 75 \ miles$

Alternatively you could have fused a fractional conversion factor of $\frac{8}{5}.$

$120 \div \frac{8}{5}=75$

Example 7: converting units of speed

Convert $45 \ km/h$ (kilometres per hour) to $m/s$ (metres per second).

Find the conversion factor.

1 \ kilometre \ = 1000 \ metres.

So the conversion factor for metres and kilometres is $1000.$

$1 \ hour \ = 60 \ seconds$

So the conversion factor for hours and minutes is $60.$

$1 \ minute \ = 60 \ seconds$

So the conversion factor for minutes and seconds is $60.$

Multiply or divide by the conversion factor.

We need to multiply by $1000$ to convert from kilometres to metres.

$45 \text{ km per hour } = 45 \times 1000=45 \ 000 \ \text{ m per hour}$

Then divide by $60$ to find out how many metres travelled in $1$ minute.

$45 \ 000 \text{ m per hour } =45 \ 000 \div 60=750 \text{ m per minute}$

Then divide by $60$ again to find out how many metres travelled in $1$ second.

$750 \text{ m per minute} =750 \div 60=12.5 \text{ m per second}$

Write down the answer.

45\ \text{km/h} = 7.5\ \text{m/s}

Alternatively, we could have done this in one calculation:

$45\ \text{km/h} = \frac{45\ \times\ 1000}{60\ \times\ 60} = 7.5\ \text{m/s}$

Common misconceptions

Fractions of an hour

Remember that time is not a decimal system based on $10.$

A quarter of an hour is $15$ minutes. But one quarter as a decimal is $0.25.$

E.g.

$3.5$ hours is $3$ hours and $30$ minutes.

$1\frac{1}{2}$ days is $1$ day and $12$ hours.

Multiply or divide

Sometimes it is difficult to know whether to multiply or divide.

E.g.

$1 \ stone \approx 6.35 \ kg$

To go from stones to kilograms we multiply by $6.35,$ and to go from kilograms to stones we divide by $6.35.$

Conversion of units Common Misconceptions Image 1

Fractional conversion factor

Be careful to get the numerator and the denominator the right way round when using a fractional conversion factor.

E.g.

When converting between miles and kilometres the conversion factor is $\frac{8}{5}.$

Conversion of units Common Misconceptions Image 2

$5 \ miles\times \frac{8 \ km}{5 \ miles}=8 \ km$

If we include the units, we can see the units cancel.

Practice conversion of units questions

300\ \text{seconds}

18\ 000 \ \text{seconds}

50\ 000 \ \text{seconds}

500\ \text{seconds}

We need to multiply by $60$ twice

5\times 60\times 60=5\times 60^2=18\ 000

So $5 \ hours$ is $18 \ 000 \ seconds$

90 \ \text{hours}

54 \ \text{hours}

5.4 \ \text{hours}

1.5 \ \text{hours}

We need to divide by $60$ twice

5\ 400\div 60\div 60=5\ 400\div (60\times 60)=5\ 400\div 60^2=1.5

So $5 \ 400 \ seconds$ is $1.5 \ hours$

1.18\ m

3.3\ m

4\ m

1.11 \ m

We need to multiply by $0.3$

3.7\times 0.3=1.11

So $3.7 \ feet$ is approximately $1.11 \ metres$

57.4 \ \text{gallons}

2.77 \ \text{gallons}

3.77 \ \text{gallons}

57.3 \ \text{gallons}

We need to divide by $4.55$

12.6\div 4.55=2.7692…=2.77

So $12.6 \ litres$ is approximately $2.77 \ gallons$ (to $3$ sf)

32 \ km

25\ km

36\ km

28\ km

We need to multiply by $\frac{8}{5}$ or $1.6$

20\times \frac{8}{5}=20\times 1.6=32

So $20 \ miles$ is approximately $32 \ km$

43\ miles

40\ miles

35 \ miles

30 \ miles

We need to divide by $\frac{8}{5}$ or $1.6$

48\div \frac{8}{5}=48\div 1.6=30

Alternatively we can to multiply by $\frac{8}{5}$ or $0.625$

48\times \frac{5}{8}=48\times 0.625=30

So $48 \ km$ is approximately $30 \ miles$

Conversion of units GCSE questions

1. $1 \ kg \approx 2.2 \ pounds$

(a) Change $8 \ kg$ to pounds

(b) Change $297 \ pounds$ to $kg.$

(4 marks)

Show answer

(a)

8\times 2.2

(1)

17.6

(1)

(b)

297\div 2.2

(1)

135

(1)

2. Use the conversion $5 \ miles \approx 8 \ km$

On Saturday mornings Elaine likes to do a jog in the park.

(a) The distance of her jog is $5 \ km.$

How far is this distance in miles?

Change $5 \ km$ to miles

(b) Elaine then drives $6 \ miles$ back home.

How far has she driven on a Saturday morning?

Give your answer in kilometres.

(4 marks)

Show answer

(a)

5\div 1.6 \ \text{or} \ 5\times 0.625

(1)

3.125 \ miles

(1)

(b)

2\times 6=12 \ miles

12\times 1.6=19.2

(1)

19.2 \ km

(1)

3. The speed limit is $80 \ km/h.$

Tariq drives at $20 \ m/s.$

Does Tariq break the speed limit?

Explain your reasoning.

(3 marks)

Show answer

20\times 60^2=72\ 000

(1)

72\ 000\div 1000 =72

(1)

$72 \ km/h$ is less than the speed limit of $80 \ km/h$ .

So Tariq does not break the speed limit.

(1)

4. Joe works in the office $3$ days each week.

He drives from his home to the office and from the office to his home.

The distance from Joe’s home to work is $15 \ miles.$

Joe’s car uses one gallon of petrol every $38 \ miles.$

$1 \ litre$ of petrol costs $154.3p$

1 \ gallon \approx 4.546 \ litres

Work out the total cost for Joe to use his car for work each week.

You must show all your working.

(5 marks)

Show answer

Weekly mileage

3\times 2\times 15=90

(1)

Weekly consumption

90\div 38=2.34842… \ gallons

(1)

2.34842…\times 4.546=10.7668…\ litres

(1)

$10.7668…\times 154.3=1661.323…$ pence

(1)

$1661$ pence or $£16.61$

(1)

Learning checklist

You have now learned how to:

Convert units of time (non-metric units)

Convert between imperial units and metric units

The next lessons are

Did you know?

Other SI units (the international system of units) include the joule (J) for power. This is much easier to use than horsepower. There is a metric horsepower and imperial horsepower which are slightly different!

There is also a metric tonne where $1$ tonne is $1000$ kilograms and also an imperial ton, which are slightly different to each other

For GCSE maths we use degrees to measure angles. However, the SI unit of measurement for angles is the radian. We use radian as a unit of measurement in A-Level maths.

In GCSE and A-Level maths we use Newtons $(N)$ for the unit of force. Newtons is a metric system. It is equivalent to $1 \ kg \ m/s^{2}$ . However there is a related unit of measurement called the dyne which is $1 \ g \ cm/s^{2}.$ We can not write the dyne with a prefix and Newtons, but $1$ Newton is $100 \ 000$ dynes.

Here are some units of measurement you may have come across in GCSE science. The SI unit for voltage is the volt $(V).$ The SI base unit for electrical current is the ampere $(A).$

There are imperial units for area and volume. For example square feet and cubic feet. We can convert square feet to square inches using the following:

1 \ square \ foot=12\times 12=12^2= 144 \ square \ inches

We can convert cubic feet to cubic inches using the following:

1 \ cubic \ foot=12\times 12\times 12=12^3= 1728 \ cubic \ inches

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.