GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
3D shapes Area of a quadrilateral Substitution Rearranging formulae Metric units of measurementThis topic is relevant for:

Volume Of Square Based Pyramid
Here we will learn about the volume of a square based pyramid, including how to calculate the volume of a square based pyramid and how to solve problems involving the volume.
There are also square based pyramid worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is volume of a square based pyramid?
The volume of a square based pyramid is how much space there is inside a square based pyramid.
A square based pyramid is a three dimensional shape made up of flat faces. It has a square base and triangular faces which meet at a point, called the apex. The vertical height is the length from the square base to the apex and is perpendicular to the base of the pyramid.
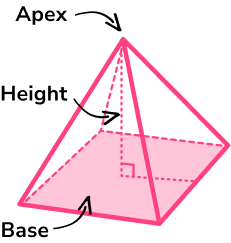
To calculate the volume of a square based pyramid we use the formula
\text{Volume}=\cfrac{1}{3}\times \text{area of base} \times \text{height} .
The pyramid height should be perpendicular to its base.
The formula can also be written as
V=\cfrac{1}{3}Bh,where
- V represents the volume of the pyramid,
- B represents the area of its base,
- h represents the perpendicular height of the pyramid.
If we are not given the perpendicular height, we can use Pythagoras’ theorem to find it from the given slant height or the lateral edge length.
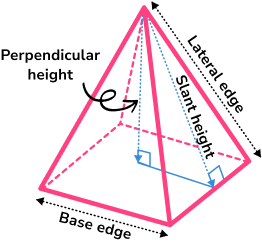
There are lots of different types of pyramids because the base of a pyramid can be any polygon.
For example, a rectangular pyramid has a rectangular base and a triangular pyramid (often known as a tetrahedron) has a triangular base.
The square pyramid formula for volume can be used for any pyramid.
What is volume of a square based pyramid?

How to calculate the volume of a square based pyramid
In order to calculate the volume of a square based pyramid:
- Calculate the area of the base.
- Substitute values into the formula and solve.
- Write the answer, including the units.
Explain how to calculate the volume of a square based pyramid

Volume and surface area of a pyramid worksheet (includes volume of square based pyramid)

Get your free volume of square based pyramid worksheet of 20+ volume and surface area of a pyramid questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Volume and surface area of a pyramid worksheet (includes volume of square based pyramid)

Get your free volume of square based pyramid worksheet of 20+ volume and surface area of a pyramid questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEVolume of square based pyramid examples
Example 1: calculating the volume, given the height, of a square pyramid
Find the volume of the square based pyramid.
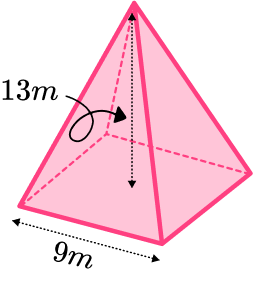
- Calculate the area of the base.
The area of the base can be found by squaring the base edge.
9^2=812Substitute values into the formula and solve.
The volume of a square based pyramid can be found by using the formula.
\begin{aligned} V&=\cfrac{1}{3}Bh \\\\ V&=\cfrac{1}{3}\times 81\times 13 \\\\ V&=351 \end{aligned}3Write the answer, including the units.
The volume is 351 \ m^{3}.
Example 2: calculating the volume, given the height, of a square pyramid
Find the volume of the square based pyramid.
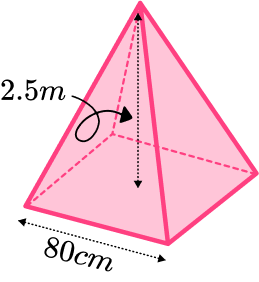
Calculate the area of the base.
The area of the base can be found by squaring the base edge.
80^2=6400
Substitute values into the formula and solve.
The volume of a square based pyramid can be found by using the formula. But the height is given in a different unit of measurement to the side of the base, 2.5 \ m is 250 \ cm.
\begin{aligned} V&=\cfrac{1}{3}Bh \\\\ V&=\cfrac{1}{3}\times 6400\times 250 \\\\ V&=533 \ 333.33… \end{aligned}
Write the answer, including the units.
The volume is 533 \ 000 \ cm^3 (to 3 sf). This can be also written as 0.533 \ m^{3}.
Example 3: calculating the volume of a square pyramid not given perpendicular height
Find the volume of the square based pyramid. The apex of the pyramid is directly above the centre of the square base.
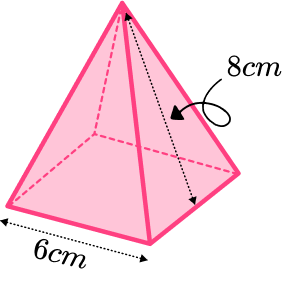
Calculate the area of the base.
The area of the base can be found by squaring the base edge.
6^2=36
Substitute values into the formula and solve.
The volume of a square based pyramid can be found by using the formula. But the perpendicular height is not given. It can be found using Pythagoras’ theorem. The slant height of the pyramid 8 \ cm is the hypotenuse.
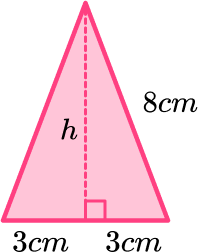
h=\sqrt{8^2-3^2}=\sqrt{55} \\
\begin{aligned} V&=\cfrac{1}{3}Bh \\\\ V&=\cfrac{1}{3}\times 36\times \sqrt{55} \\\\ V&=12\sqrt{55} \\\\ V&=88.9943… \end{aligned}
Write the answer, including the units.
The volume is 89.0 \ cm^3 (to 3 sf).
Example 4: calculating the volume of a square pyramid not given perpendicular height
Find the volume of the square based pyramid. The apex of the pyramid is directly above the centre of the square base.

Calculate the area of the base.
The area of the base can be found by squaring the base edge.
14^2=196
Substitute values into the formula and solve.
The volume of a square based pyramid can be found by using the formula. But we do not know the perpendicular height. We have been given the lateral edge length. We will need to apply Pythagoras’ theorem twice to find the perpendicular height.
The value 7 comes from using the midpoint of the base edge to make right angled triangles.
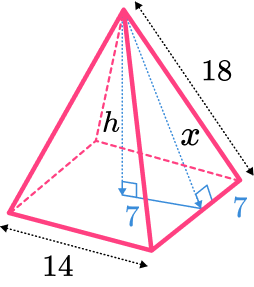
First we find the slant length from the lateral edge length.
x=\sqrt{18^2-7^2}=5\sqrt{11}
Then we can find the perpendicular height of the square based pyramid.
h=\sqrt{(5\sqrt{11})^2-7^2}=\sqrt{226} \\
\begin{aligned} V&=\cfrac{1}{3}Bh \\\\ V&=\cfrac{1}{3}\times 196\times \sqrt{226} \\\\ V&=982.175… \end{aligned}
Write the answer, including the units.
The volume is 982 \ m^3 (to 3 sf).
Example 5: calculating the height given the volume
The volume of the square based pyramid is 87.6 \ cm^{3}. Find the perpendicular height, h. Give your answer to 3 significant figures.
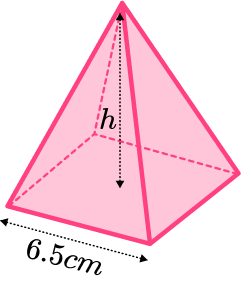
Calculate the area of the base.
The area of the base can be found by squaring the base edge.
6.5^2=42.25
Substitute values into the formula and solve.
The formula for the volume of the square based pyramid can be used to find the perpendicular height, h.
\begin{aligned} V&=\cfrac{1}{3}Bh \\\\ 87.6&=\cfrac{1}{3}\times 42.25\times h \\\\ h&=\cfrac{87.6\times 3}{42.25} \\\\ h&=6.2201… \end{aligned}
Write the answer, including the units.
The perpendicular height h is 6.22 \ cm (to 3 sf).
Example 6: calculating the length of the base given the volume
The volume of the square based pyramid is 1200 \ m^{3}. Find the base edge. Give your answer correct to 1 decimal place.
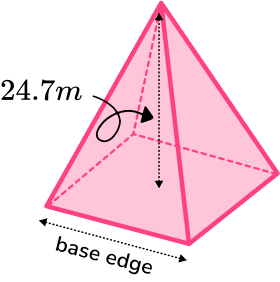
Calculate the area of the base.
The area of the base can not be found yet. But, when we find it we can square root it to find the length of the base (the base edge).
Substitute values into the formula and solve.
The formula for the volume of the square based pyramid can be used to find the base area.
\begin{aligned} V&=\cfrac{1}{3}Bh \\\\ 1200&=\cfrac{1}{3}\times B\times 24.7 \\\\ h&=\cfrac{1200\times 3}{24.7}\\\\ h&=145.7489… \end{aligned}
We can then square root the base area to find the length of the base.
\sqrt{145.7489…}=12.072…
Write the answer, including the units.
The length of the base is 12.1 \ m (to 1 dp).
Common misconceptions
- The height is the perpendicular height
The height of a square pyramid needs to be the perpendicular height. This is the height that is at a right-angle to the base.
- Use the correct units
Remember to use cubic units for volume such as cm^{3} or m^{3}. Square units such as cm^{2} or m^{2} are for areas.
- Use the correct volume formula
There are many different volume formulas in maths. Make sure that you use the correct one to work out the volume of a pyramid.
\text{Volume}=\cfrac{1}{3}\times \text{area of base} \times \text{height}
Or
V=\cfrac{1}{3}Bh
- Be accurate
When there are two or more steps in your workings, do not round your workings. Only round at the end of your solution so that your answer is accurate.
- Take care with rounding
At the end of the question, make sure you round your answer to the correct number of decimal places or significant figures.
Related lessons
Volume of a pyramid is part of our series of lessons to support revision on pyramids. You may find it helpful to start with the main pyramid lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Practice volume of square based pyramid questions
1. Work out the volume of this square based pyramid.
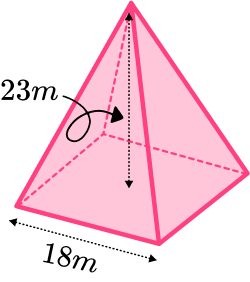




We can work out the volume of a pyramid by using the formula
V=\cfrac{1}{3}Bh.
The base area can be found by squaring the side length of the base square.
18^2=324
We can substitute the values we have been given into the formula and work out the volume.
V=\cfrac{1}{3}\times 324 \times 23=2484
So the volume is 2484 \ m^{3}.
2. Work out the volume of this square based pyramid. Give your answer in cm^{3}.
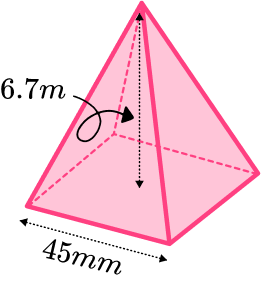




We can work out the volume of a pyramid by using the formula
V=\cfrac{1}{3}Bh.
The base area can be found by squaring the side length. The side length is in mm so needs converting the cm.
4.5^2=20.25
The height of 6.7 \ m needs to be converted to 670 \ cm .
We can substitute the values we have been given into the formula and work out the volume.
V=\cfrac{1}{3}\times 20.25 \times 670=4522.5
So the volume is 4522.5 \ cm^{3} .
3. Work out the volume of this square based pyramid. Give your answer in cm^{3} correct to three significant figures.
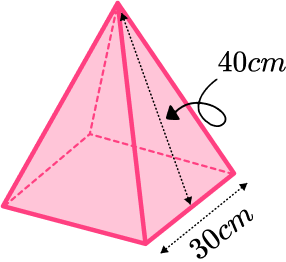




We can work out the volume of a pyramid by using the formula
V=\cfrac{1}{3}Bh.
The base area can be found by squaring the side length.
30^2=900
We have been given the slant length. We can use this to find the perpendicular height of the pyramid.
h=\sqrt{40^2-15^2}=5\sqrt{55}
We can substitute the values we have been given into the formula and work out the volume.
V=\cfrac{1}{3}\times 900 \times 5\sqrt{55}=11124.29…
So the volume is 11 \ 100 \ cm^{3} (to 3 sf).
4. Work out the volume of this square based pyramid. V is directly above B and VC is 10 \ cm. Give your answer in cm^{3}.
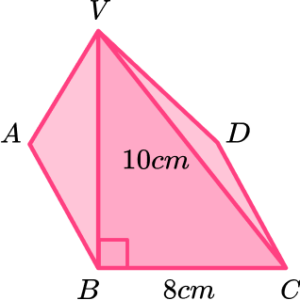




We can work out the volume of a pyramid by using the formula
V=\cfrac{1}{3}Bh.
The base area can be found by squaring the side length.
8^2=64
We have been given a slant length. We can use this to find the perpendicular height of the pyramid.
h=\sqrt{10^2-8^2}=6
We can substitute the values we have been given into the formula and work out the volume.
V=\cfrac{1}{3}\times 64 \times 6=128
So the volume is 128 \ cm^{3} .
5. The volume of this square based pyramid is 460 \ cm^{3}. Find the perpendicular height of the pyramid. Give your answer correct to 3 significant figures.
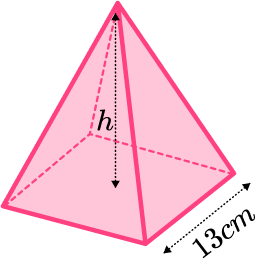




We can substitute the values we are given into volume of a pyramid formula and rearrange it to find the height, h.
\begin{aligned} V&=\cfrac{1}{3}Bh \\\\ 460&=\cfrac{1}{3}\times 13^2\times h \\\\ h&=\cfrac{460\times 3}{13^2} \\\\ h&=8.1656… \end{aligned}
So the perpendicular height is 8.17 \ cm^{3} (to 3 sf).
6. The volume of this square based pyramid is 8900 \ mm^{3}. Find the side length of the pyramid. Give your answer correct to 3 significant figures.
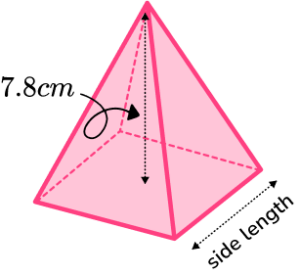




We can substitute the values we are given into the volume of a pyramid formula and rearrange it to find the base area.
The perpendicular height is given in cm, so needs converting to mm.
\begin{aligned} V&=\cfrac{1}{3}Bh \\\\ 8900&=\cfrac{1}{3}\times B\times 78 \\\\ B&=\cfrac{8900\times 3}{78}\\\\ B&=342.3076… \end{aligned}
The area of the base needs to be square rooted to find the side length.
\sqrt{342.3076…}=18.501…
So the perpendicular height is 18.5 \ mm (to 3 sf).
Volume of square based pyramid GCSE questions
1. The diagram shows a square based pyramid.
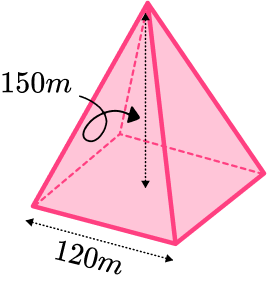
Calculate the volume of the square based pyramid.
Give your answer correct to 3 significant figures
Give the correct units for your answer.
(4 marks)
Area of the base is 120^{2}=14400 .
(1)
\cfrac{1}{3} \times 14400 \times 150(1)
720 \ 000(1)
m^3(1)
2. The diagram shows a square based pyramid.
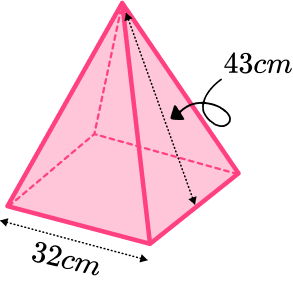
Calculate the volume of the square based pyramid.
Give your answer correct to 3 significant figures
(4 marks)
Area of the base is 32^{2}=1024 .
(1)
h=\sqrt{43^{2}-16^{2}}=39.912…(1)
\cfrac{1}{3} \times 1024 \times 39.912…=13623.4…(1)
13600 \ cm^3(1)
3. The diagram shows a square based pyramid.
It is based on one of the pyramids of Giza.
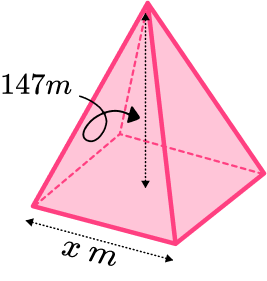
It has a volume of 2.6 million m^{3}.
It has a height of 147 \ m.
Find the side length, x of its square base.
Give your answer to 3 significant figures
(4 marks)
2.6 million = 2 \ 600 \ 000
(1)
\cfrac{2 \ 600 \ 000 \times 3}{147}=53061.224…(1)
\sqrt{53061.224…}=230.35…(1)
230 \ m(1)
4. The diagram shows a truncated square pyramid.

Find the volume of the truncated square based pyramid.
Give your answer as an exact value.
(5 marks)
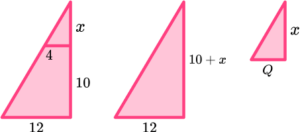
For using similar triangles to find the missing height.
(1)
For the height of large pyramid or the height of small pyramid, 15 \ cm and 5 \ cm.
(1)
For the volume of large pyramid or the volume of small pyramid, 720 or 26\cfrac{2}{3}.
(1)
720-26\cfrac{2}{3}(1)
693\cfrac{1}{3} \ cm^3(1)
Learning checklist
You have now learned how to:
- Recognise a square based pyramid and its features
- Calculate the volume of a square based pyramid
- Solve problems involving volume
- Find the total surface area of a square based pyramid
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.