GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
Scale drawing Constructions Perpendicular bisector Angle bisectorThis topic is relevant for:

Loci
Here we will learn about loci, including drawing loci and describing loci.
There are also loci worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are loci?
Loci are the set of points or regions that satisfy a property or rule.
To draw loci we will need to use constructions such as perpendicular bisectors and angle bisectors.
Construct loci
There are some standard loci that we will be required to be able to draw:
- Equidistant from a fixed point (an arc or circle)
- Equidistant from two fixed points (perpendicular bisector)
- Equidistant from a straight line
- Equidistant from two intersecting straight lines (an angle bisector)
What are loci?
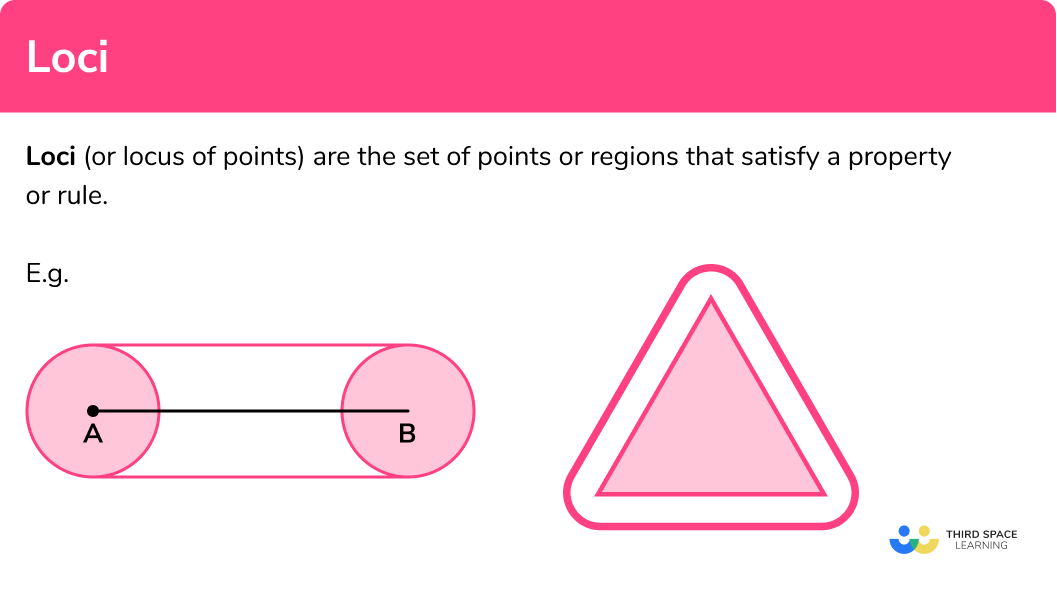
How to draw loci
In order to draw loci:
- Use the wording of the region required to decide what constructions are needed.
- Perform any relevant constructions for points or line segments involved.
- Indicate the region required as necessary.
How to draw loci

Loci worksheet

Get your free loci worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Loci worksheet

Get your free loci worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on loci and constructions
Loci is part of our series of lessons to support revision on loci and construction. You may find it helpful to start with the main loci and construction lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Loci examples
Example 1: locus of points around a fixed point
Draw the locus of the points 4 cm from point P.
- Use the wording of the region required to decide what constructions are needed.
The locus of points equidistant from a point is a circle.
2Perform any relevant constructions for points or line segments involved.
Draw a circle, radius 4cm using point P as the centre using a compass.
3Indicate the region required as necessary.
We want the points 4cm from P so the circumference of the circle is required.
Example 2: locus of points around a straight line
Shade the region within 3 cm of the line segment AB.
Use the wording of the region required to decide what constructions are needed.
The locus of points equidistant from a line will need lines parallel to the line segment and semicircles at the end points.
Perform any relevant constructions for points or line segments involved.
Begin by drawing circles, radius 3cm at the end points using A and B as the centres.
Then, using the circle add the parallel lines 3cm away from the line segment AB.
Indicate the region required as necessary.
We want the region within 3cm of AB so shade the inside of the shape.
Example 3: locus of points around a straight line
Draw the locus of the points 2 cm outside of the equilateral triangle.
Use the wording of the region required to decide what constructions are needed.
The locus of points equidistant from a polygon will need lines parallel to the sides of the triangle and arcs of the same radius at the vertices.
Perform any relevant constructions for points or line segments involved.
Draw arcs, radius 2cm using each vertex as the centres. Ensure these arcs span a suitable angle.
Then, using the arcs as a guide add the lines 2cm away and parallel to the line segments .
Indicate the region required as necessary.
Erase any unnecessary lines to make the arcs and straight lines join.
Example 4: locus of points around a straight line
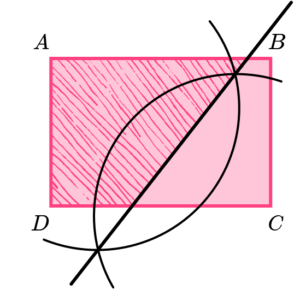
For the rectangle ABCD, shade the region inside which is closer to point A than point C.
Use the wording of the region required to decide what constructions are needed.
For a region closer to one point than another we need to first draw the line equidistant to the two points.
The locus of points equidistant from two points is a perpendicular bisector.
Perform any relevant constructions for points or line segments involved.
Draw a perpendicular bisector of points A and C.
Indicate the region required as necessary.
We want the points closer to A than C so shade the region above the perpendicular bisector.
Example 5: locus of points equidistant to two intersecting straight lines
For the rectangle ABCD, draw the locus of the points equidistant from AB and AD.
Use the wording of the region required to decide what constructions are needed.
The locus of points equidistant from AB and AD is an angle bisector.
Perform any relevant constructions for points or line segments involved.
Draw and angle bisector of the angle BAD.
Indicate the region required as necessary.
We want the points equidistant from AB and AD, so the line is required.
Example 6: combination of loci
Shade the region which is closer to point R than point Q, but within 3cm of point P.
Use the wording of the region required to decide what constructions are needed.
We will need to draw a perpendicular bisector of Q and R, and then a circle radius 3cm with P as the centre.
Perform any relevant constructions for points or line segments involved.
Construct a perpendicular bisector of QR.
Now draw a circle, radius 3cm using point P as the centre.
Indicate the region required as necessary.
We want the region which is closer to point R than point Q, but within 3cm of point P, therefore we must shade the region below the perpendicular bisector which is inside the circle.

Common misconceptions
- Incorrect locus at the corner of a shape
A common error occurs when drawing the locus of points, a fixed distance from the perimeter of a polygon. It is important to remember that the vertex of a polygon must be treated in the same way as a fixed point. Therefore, an arc must be used for the locus at the vertex.
E.g.
- Joining corners of rectangles instead of bisecting the angle
A common error occurs when asked to find the locus of points equidistant from two perpendicular sides of a rectangle. The error is to just join the opposite corners of the rectangle instead of performing an angle bisector.
E.g
The locus of the points equidistant from AB and AD.
Practice loci questions
1. What diagram describes the locus of the points equidistant from the point P?




The points equidistant from another point form a circle.
2. What diagram describes the locus of the points a fixed distance from the perimeter of the triangle ABC?




The needs to be arcs at each vertex, if the question does not state that the locus is only inside or outside, both loci should be shown.
3. What should you construct to draw the locus of the points equidistant from the points P and Q?
An angle bisector

A circle

Join points P and Q with a line segment

A perpendicular bisector

The locus of points equidistant to two points is a perpendicular bisector of the line segment between them.
4. What diagram describes the points equidistant from the line segment MN?




The points equidistant from a line segment will consist of lines parallel to the line segment and semicircles at each end.
5. What diagram describes the region closer to the line AB than the line AC?

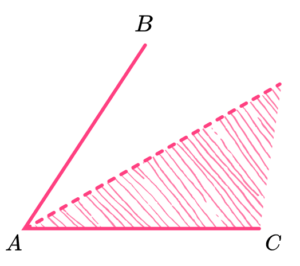




To be closer to AB than AC, you must bisect the angle BAC and then shade the region closer to AB.
6. What diagram describes the region within 2cm of points A and B and within 3 cm of point C?
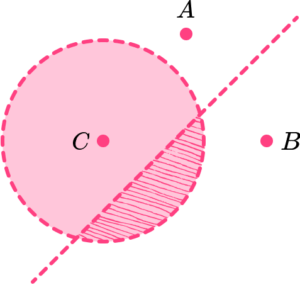

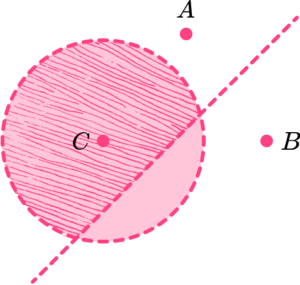



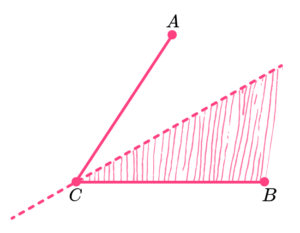

Draw circles radius 2cm around A and B. Draw a circle radius 3cm around C. Shade in the region where the circles intersect.
Loci GCSE questions
1. A campsite needs to install a new water tap. It must be closer to reception than the shower block, but within 30 metres of the shower block.
Using a scale of 1cm to 5 metres, indicate the region where the water tap can be installed.
(3 marks)
Perpendicular bisector drawn
(1)
Circle radius 6 cm drawn with shower block as the centre
(1)
Correct region indicated/shaded
(1)
2. The diagram shows positions of a wifi router and wifi extender in a floor plan of a single storey house. The wifi router has a range of 8 metres and the wifi extender has a range of 6 metres.
Show on the diagram the regions where the wifi router and wifi extender do not reach. Use a scale of 1cm to 2 metres.
(3 marks)
Circle radius 4cm around wifi router
(1)
Circle radius 3cm around wifi extender
(1)
Correct regions indicated/shaded
(1)
3. The diagram shows the plan of a beach and pier. The town council wants to section off some areas of the beach and water for activities and safety. They plan to use floating ropes to mark the areas that are safe for swimming and the areas that are for pedal boats only.
Swimmers must stay 20 metres away from the rocks and be closer to the beach than the pier. They must also stay 30 metres away from the pedal boat station.
Show on the diagram, using a scale of 1cm to 10 metres, the region that is safe for swimmers.
(4 marks)
Learning checklist
You have now learned how to:
- Use the standard ruler and compass constructions
- Construct perpendicular bisector of a line segment
- Construct a perpendicular to a given line from/at a given point
- Bisect a given angle
- Use constructions to solve loci problems
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.