2. Which diagram correctly shows how to construct the angle bisector of angle $ABC$?

3. Which diagram shows the locus of points a distance of $ d $ from the triangle?

Loci and construction

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

Angle rules Angles around a point Angles in a triangle Angles in parallel lines Trigonometry

This topic is relevant for:

GCSE Maths Geometry and Measure

Loci And Construction

Here we will learn about loci, constructions and bearings, including drawing various constructions, using constructions when drawing loci and measuring and calculating bearings.

There are also loci & construction worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are loci and construction?

Loci and construction are geometric objects that are drawn with specific features.

To draw loci and constructions accurately, you will be required to use a ruler, a pair of compasses, and a protractor when appropriate.

A ruler is used to measure distances and construct straight lines.
A pair of compasses is used to draw points that are a fixed distance from a point.
A protractor is used to measure and construct angles.

Constructions are set methods for creating accurate drawings in maths.

A locus of points (plural loci) is a set of points that follow a given rule. We often use constructions to accurately draw loci.

A bearing is an angle, measured clockwise from north, used to describe the position of an object. Bearings are given using three figures, for example $052^{\circ}.$

What are loci and construction?

● Constructions

There are a number of different constructions that you need to be able to perform for GCSE maths. These include,

Angle bisector
Perpendicular bisector of a straight line
Perpendicular line to or from a particular point
Triangles, given information about sides and/or angles
Polygons

To do constructions we carefully follow the method, leaving all construction lines visible.

The most common constructions are,

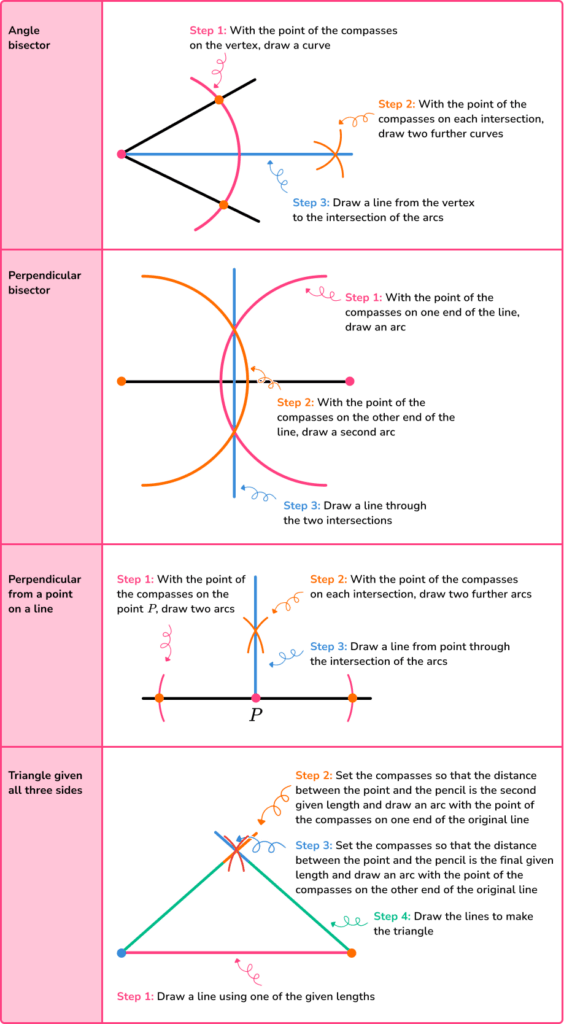
When doing constructions, all construction lines should be left visible.

Step-by-step guide: Constructions

● Loci

A locus of points (plural loci) is a set of points that follow a given rule. Given a rule, we need to be able to identify the points that follow that rule.

Here are some examples,

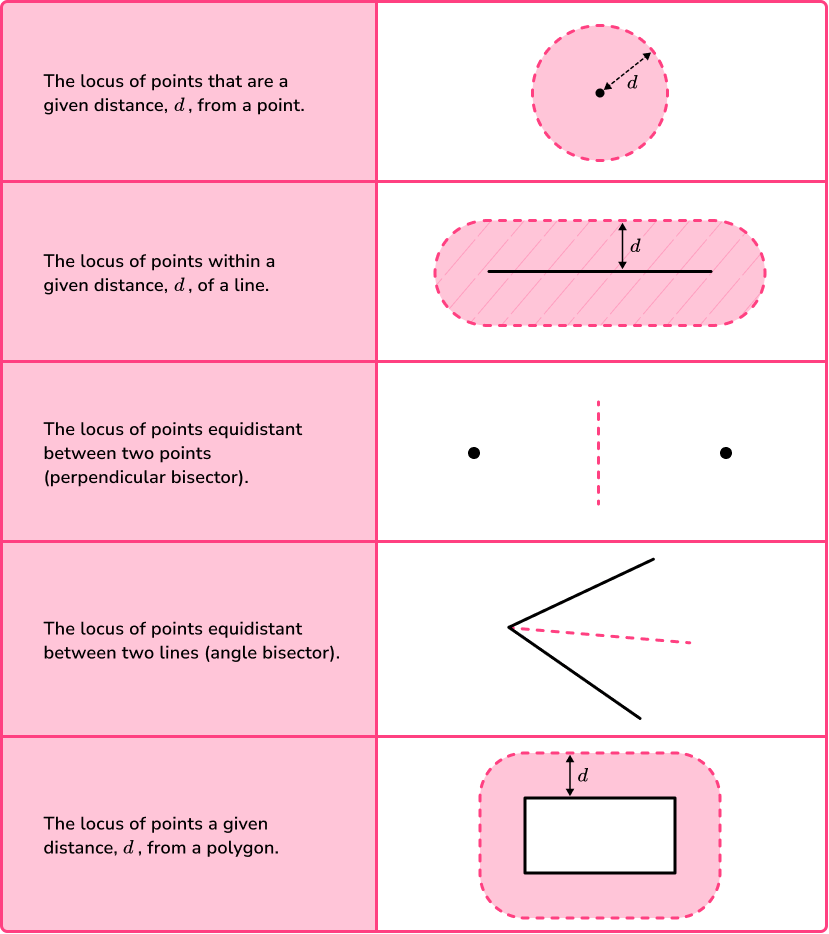
Step-by-step guide: Loci

Bearings

A bearing is an angle, measured clockwise from north, used to describe the position of an object. They are written using three figures. Bearings can be drawn, measured or calculated depending on the problem.

The bearing of B from A is $075^{\circ}.$ This means to get from A to B, you need to travel in a direction $75^{\circ}$ clockwise from north.

We can find the bearing of A from B using angle rules.

As both north lines in the diagram below are in the same direction, these lines are parallel. This means that the angle at A and the angle at B are co-interior (their angle sum is $180^{\circ}$ ).

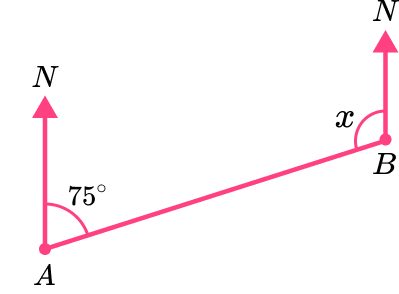
The angle $x$ is equal to $180-75=105^{\circ}.$

The back bearing is the bearing of A from B. As the sum of angles at a point is $360^{\circ},$ the bearing $\theta$ of A from B in the diagram below is $360-105=255^{\circ}.$

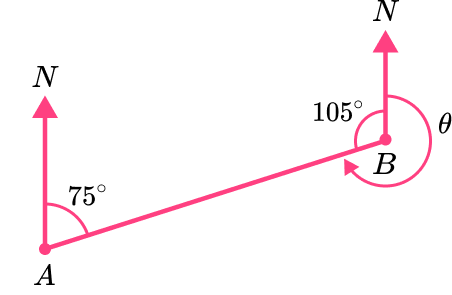
Step-by-step guide: Bearings

How to use loci and constructions

Loci and construction worksheet

Get your free loci and construction worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Loci and construction worksheet

Get your free loci and construction worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Loci and construction examples

Example 1: bisect an angle

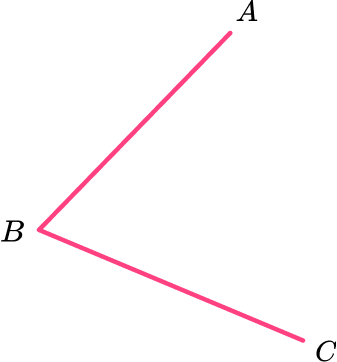
Bisect the angle ABC.

Loci And Construction bearings example 1 image

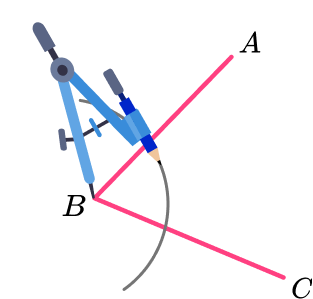
With the point of the compasses on the vertex, draw an arc.

Loci And Construction bearings example 1 step 1

2With the point of the compasses on each intersection, draw two further arcs.

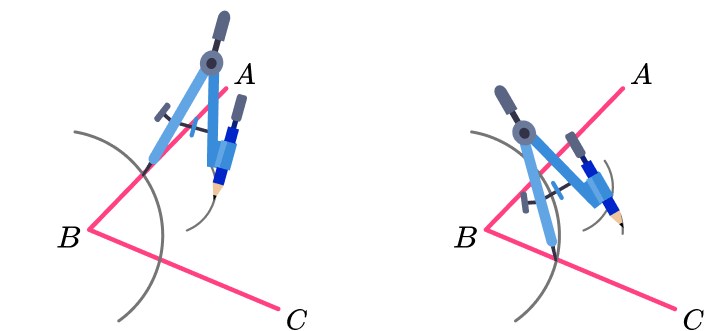
Loci And Construction bearings example 1 step 2

3Draw a line from the vertex to the intersection of the arcs.

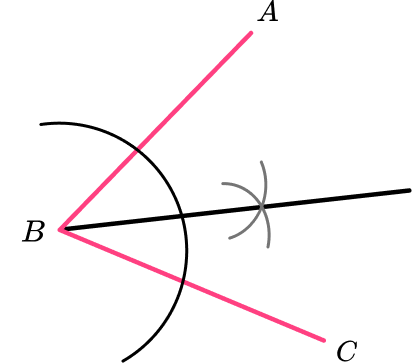
Loci And Construction bearings example 1 step 3

Step-by-step guide: Angle bisector

Example 2: locus of points equal distance from two points (perpendicular bisector)

Draw the locus of points equidistant from lighthouse $A$ and lighthouse $B$ .

Loci And Construction bearings example 2 image 1

The locus of points equidistant from two points is the perpendicular bisector of the line between those points. Imagine a straight line connecting the two points $A$ and $B$ .

We need to construct the perpendicular bisector of the line $AB$ .

Loci And Construction bearings example 2 image 2

With the point of the compasses on one end of the line, draw an arc.

Here we will place the point of the compass at $A$ and draw an arc.

The radius of the arc must be greater than half of the distance between $A$ and $B$ .

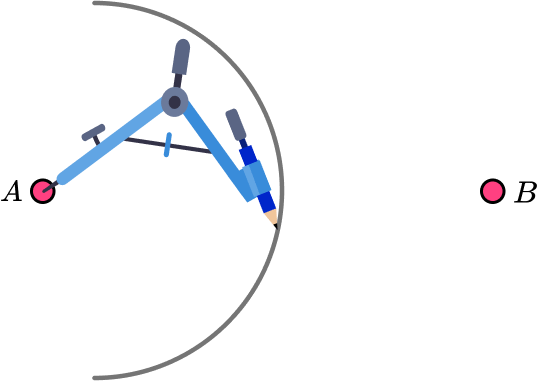
Loci And Construction bearings example 2 step 1

With the point of the compasses on the other end of the line, draw a second arc.

Placing the point of the compass at $B$ , we construct another arc with the same radius as the previous arc.

The radius of each arc must be the same, otherwise the two points of intersection will not be the same distance from $A$ and $B$ .

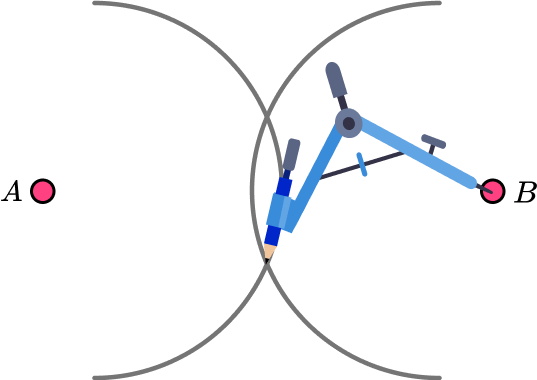
Loci And Construction bearings example 2 step 2

Draw a straight line through the two points where the arcs cross.

Using a ruler, draw a straight line through both pairs of intersecting arcs.

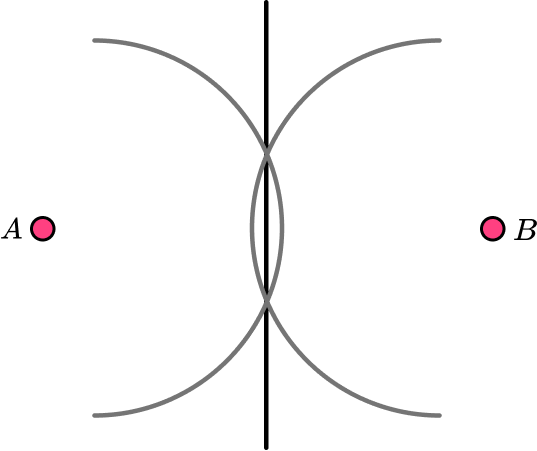
Loci And Construction bearings example 2 step 3

The line we have drawn is the locus of points equidistant from $A$ and $B$ .

Step-by-step guide: Perpendicular bisector

Example 3: combined loci problem (distance from a point)

Two phone masts, $R$ and $S$ are $50 \ km$ apart. The signal from phone mast $R$ can reach $30 \ km$ and the signal from phone mast $S$ can reach $35 \ km.$ Using the scale $1 \ cm=10 \ km,$ shade the area covered by signal from both phone masts.

Loci And Construction bearings example 3

Use the wording of the region required to decide what constructions are needed.

In this case, we need to draw a circle with radius $3 \ cm$ (to represent $30 \ km$ ) around mast $R$ and a circle with radius $3.5 \ cm$ (to represent $35 \ km$ ) around mast $S$ .

Perform any relevant constructions for points or line segments involved.

For the first circle with centre $R$ , measure the distance between the point of the compass and the pencil to $3 \ cm$ using a ruler. Place the point of the compasses on $R$ and draw a circle. The radius of this circle is $3 \ cm.$

For the second circle with centre $S$ , measure the distance between the point of the compasses and the pencil to $3.5 \ cm$ using a ruler. Place the point of the compasses on $S$ and draw a circle. The radius of this circle is $3.5 \ cm.$

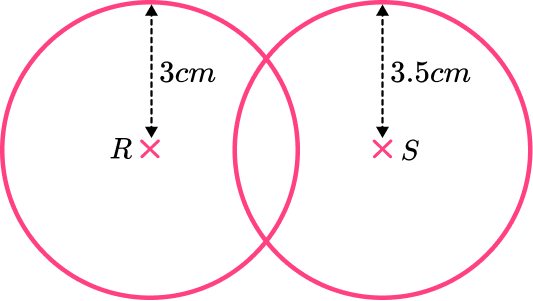
Loci And Construction bearings example 3 step 2

Indicate the region required as necessary.

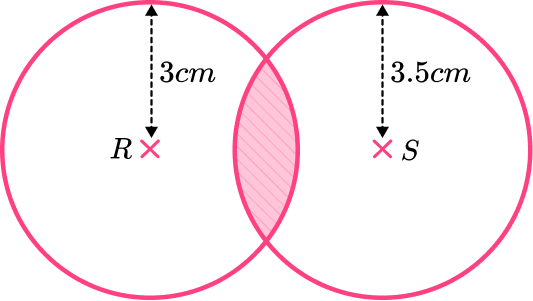
Loci And Construction bearings example 3 step 3

The shaded area is covered by signals from both phone masts.

Step-by-step guide: Constructions between points and lines

Example 4: combined loci problem (distance from a line)

Below is a diagram of Ellie’s garden. Ellie wants to plant a new tree. She wants the tree to be closer to the side $AD$ than the side $AB$ , more than $2 \ m$ from $A$ and less than $3 \ m$ from the side $AB$ . Using the scale $1 \ cm=1 \ m,$ indicate the area in which Ellie can plant the tree.

Loci And Construction bearings example 4

Use the wording of the region required to decide what constructions are needed.

Breaking down the wording of the question we have the following three facts,

closer to the side $AD$ than the side $AB$ ,
more than $2 \ m$ from $A$ ,
less than $3 \ m$ from the side $AB$ .

To determine the points closer to the side $AS$ than the side $AB$ , we need to construct an angle bisector. This is because all of the points that are on the angle bisector are the same distance from both lines, and so points in one half will be closer to one line than the other.

To determine the points more than $2 \ m$ from $A$ , we need to construct a circle with radius $2 \ cm.$ This is because $A$ is a point and we need all the points beyond $2 \ m$ from $A$ .

To determine the points less than $3 \ m$ from the side $AB$ , we need to construct a parallel line that is $3 \ cm$ from the line $AB$ .

Perform any relevant constructions for points or line segments involved.

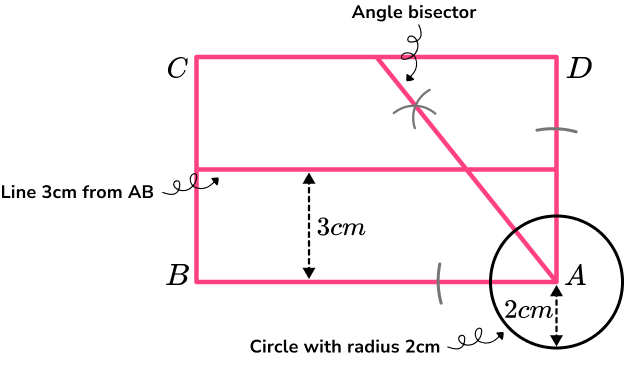
Loci And Construction bearings example 4 step 2

Indicate the region required as necessary.

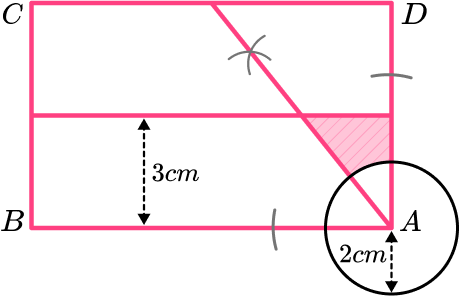
Loci And Construction bearings example 4 step 3

The shaded area is the locus of points which satisfy all of Ellie’s criteria,

closer to the side $AD$ than the side $AB$ ,
more than $2 \ m$ from $A$ ,
less than $3 \ m$ from the side $AB$ .

Example 5: draw a bearing

The bearing of a ship from lighthouse $A$ is $130^{\circ}.$ The bearing of the same ship from lighthouse $B$ is $025^{\circ}.$ Mark the position of the ship on the diagram.

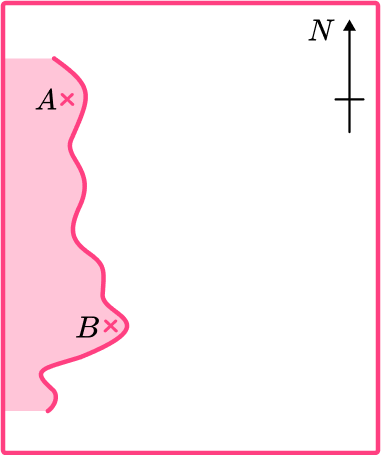
Loci And Construction bearings example 5

Locate the point you are measuring the bearing from and draw a north line if there is not already one given.

We need to draw bearings from both points $A$ and $B$ so both need a north line.

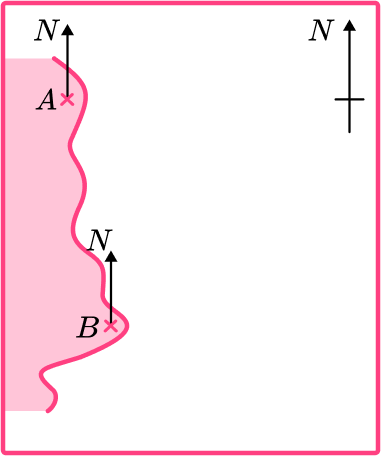
Loci And Construction bearings example 5 step 1

Using your protractor, place the zero of the scale on the north line and measure the required angle clockwise, make a mark on your page at the angle needed.

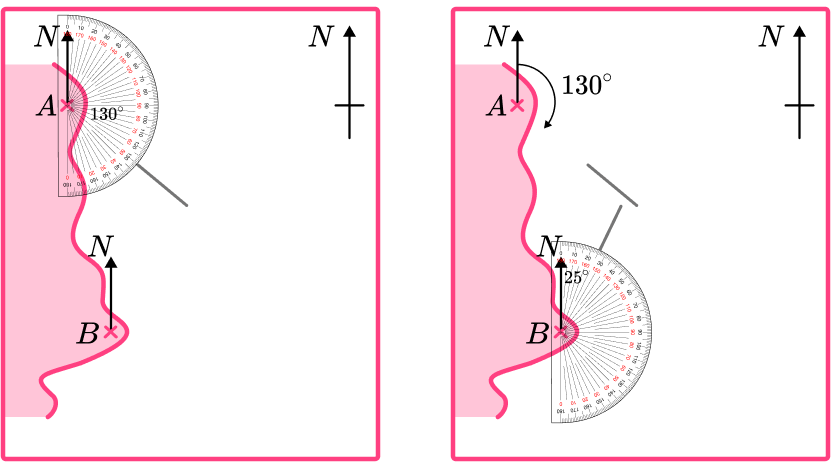
Loci And Construction bearings example 5 step 2

Draw a line from the start point in the direction of the bearing. If you are producing a scale drawing and know the distance to locate a point use this scale appropriately.

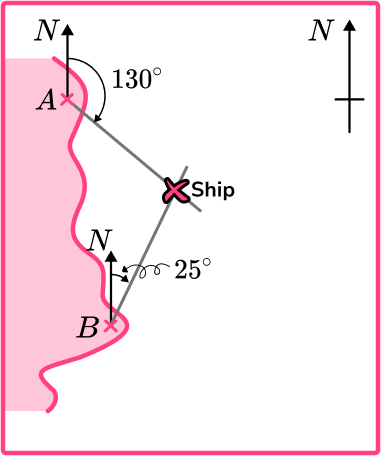
Loci And Construction bearings example 5 step 3

The ship is located at the point where the two lines intersect.

Example 6: calculate a bearing

A plane starts at airport $A$ . The plane flies $40 \ km$ east and then $60 \ km$ north before landing at airport $B$ . Find the bearing of airport $B$ from airport $A$ .

Locate the points you are calculating the bearing from and to.

Drawing a diagram is very helpful here.

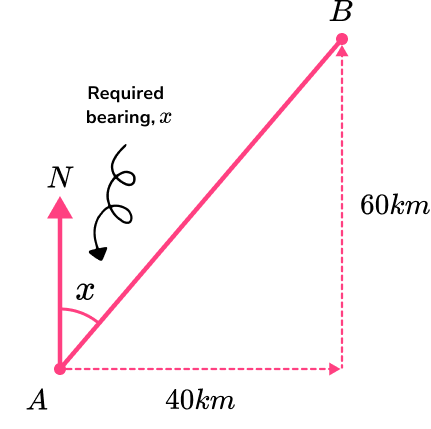
Loci And Construction bearings example 6 step 1

Using the north lines for reference at both points, use angle rules and/or trigonometry to calculate any angles that are required.

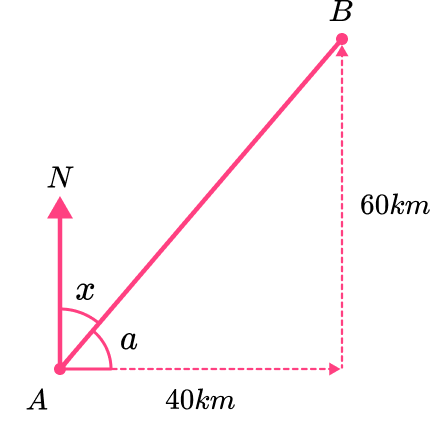
Loci And Construction bearings example 6 step 2

We can find angle $a$ using SOHCAHTOA and then use angle facts to determine angle $x.$

$\begin{aligned} \tan (a) &=\frac{60}{40}\\\\ a&=\tan ^{-1} (\frac{60}{40})\\\\ a&=56^{o} \end{aligned}$

As the sum of angles in a right angle is $90$ degrees, we can find the missing angle $x$ by subtracting $56$ from $90$ to get $90-56=34^{\circ}$

Read off the three-figure bearing required.

Converting the angle of $34^{\circ}$ to a three-figure bearing gives us the solution $034^{\circ}.$

Step-by-step guide: Constructing triangles

See also: How to draw a hexagon

Common misconceptions

Removing construction lines

When drawing constructions, the construction lines must be shown and not erased.

Corners when drawing the locus around a polygon or line

When drawing the locus around a polygon or a line, the locus around a vertex should be an arc. For example,

Loci And Construction bearings common misconceptions image 1

Connecting the corners instead of bisecting an angle

When finding the locus of points equidistant from two sides of a rectangle, we need to bisect the angle rather than drawing a line between the two corners.

For example,

Loci And Construction bearings common misconceptions image 2

Not measuring bearings from north

It is important to remember that bearings are always measured from north.

Not measuring bearings in a clockwise direction

Bearings must be measured in a clockwise direction.

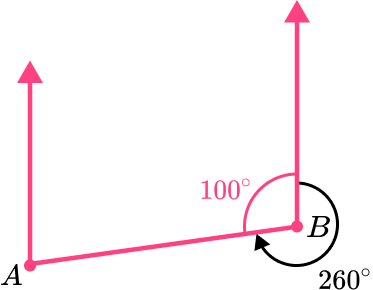
For example, the bearing of $A$ from $B$ is $360-100=260^{\circ},$ not $100^{\circ}.$

Loci And Construction bearings common misconceptions image 3

Practice loci and construction questions

Angle bisector of the angle $AB$

Perpendicular to the line $AB$ at the point $P$

Perpendicular bisector of the line $AB$

Triangle $ABC$

The two straight lines are at right angles to each other and so they are perpendicular lines. Also, the radius of each arc from $A$ and $B$ is the same and so the line is bisected into two equal halves.

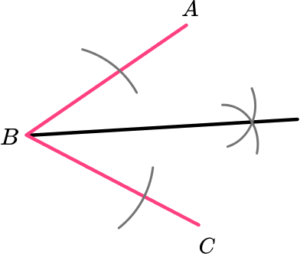
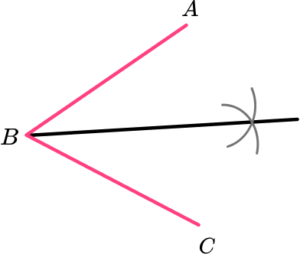
Loci And Construction bearings practice question 2

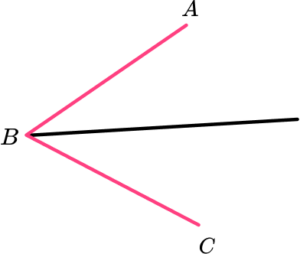
Loci And Construction bearings practice question 2 c

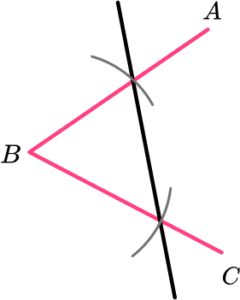
Loci And Construction bearings practice question 2 d

An arc of the same radius is drawn on line $AB$ and $BC$ from the point $B$ . From these arcs, two intersecting arcs are drawn with a straight line connecting the vertex at $B$ and the intersection point.

Loci And Construction bearings practice question 3

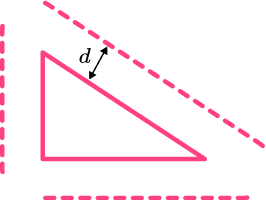
Loci And Construction bearings practice question 3 answer 1

Loci And Construction bearings practice question 3 answer 2

Loci And Construction bearings practice question 3 answer 3

Each vertex should be treated as a point and therefore the locus around each vertex should be an arc. The locus of points from a line are parallel.

Loci And Construction bearings practice question 4 answer 1

Loci And Construction bearings practice question 4 answer 2

Loci And Construction bearings practice question 4 answer 3

Loci And Construction bearings practice question 4 answer 4

We need to draw a circle with radius $2 \ cm$ around the point $B$ and the angle bisector of angle $BAD$ . The shaded region is outside of the circle and to the left side of the line drawn for the angle bisector.

065^{\circ}

115^{\circ}

295^{\circ}

025^{\circ}

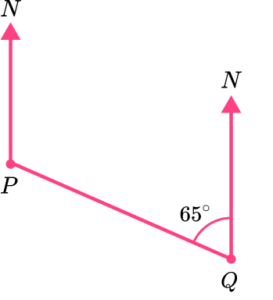
Bearings are measured clockwise from north. The bearing of $P$ from $Q$ is $360-65=295^{\circ}.$

260^{\circ}

280^{\circ}

80^{\circ}

190^{\circ}

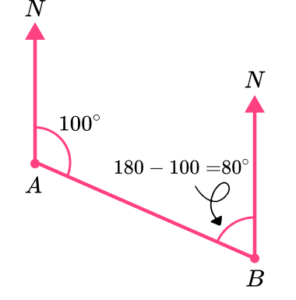
Loci And Construction bearings practice question 6

By drawing a diagram, we can see that the co-interior angle at $B$ is $180-100=80^{\circ}$ (remember that all north lines are parallel). Therefore the bearing of $A$ from $B$ , measured clockwise from north, is $360-80=280^{\circ}.$

Loci and construction GCSE questions

1. Construct the perpendicular to the line $AB$ at the point $P$ .

(3 marks)

Show answer

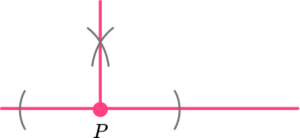
Loci And Construction bearings GCSE Question 2

Two arcs equidistant from $P$ .

(1)

Two further arcs above (or below) $P$ .

(1)

Perpendicular drawn and all construction lines shown.

(1)

2. Shade the area that is closer to the side $AB$ than the side $BC$ and is closer to the point $B$ than the point $A$ .

Loci And Construction bearings GCSE Question 2 image 1

(3 marks)

Show answer

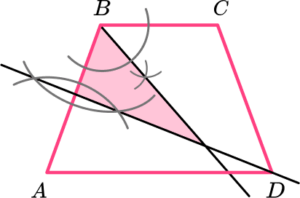
Loci And Construction bearings GCSE Question 2 image 2

Perpendicular bisector of $AB$ .

(1)

Angle bisector of angle $ABC$ .

(1)

Correct area shaded.

(1)

3. Some rangers are tracking the position of a lion.

The lion is on a bearing of $055^{\circ}$ from ranger $A$ and $290^{\circ}$ from ranger $B$ .

Mark the position of the lion on the diagram below.

Loci And Construction bearings GCSE Question 3

(3 marks)

Show answer

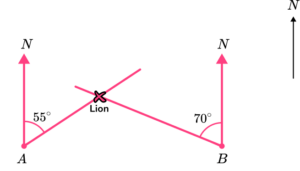
Loci And Construction bearings GCSE Question 3 image 2

Bearing of $055^{\circ}$ from $A$ drawn.

(1)

Bearing of $290^{\circ}$ from $B$ drawn.

(1)

Position of lion marked.

(1)

Learning checklist

You have now learned how to:

Derive and use the standard ruler and compass constructions (perpendicular bisector of a line segment, constructing a perpendicular to a given line from/at a given point, bisecting a given angle); recognise and use the perpendicular distance from a point to a line as the shortest distance to the line

Interpret and use bearings

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.