GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

Vector notation Vector addition Vector subtraction Fractions

Ratio and proportion

Properties of 2D shapes

This topic is relevant for:

GCSE Maths Geometry and Measure Vectors

Vector problems

Vector Problems

Here we will learn about more difficult vector problems, including vector routes involving midpoints, fractions and ratios of lengths. We will also look at parallel vectors.

There are also vector worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are vector problems?

Vector problems use vectors to solve a variety of different types of problems. Vectors have both a magnitude and direction and can be used to show a movement. A quantity which has just magnitude (size) is called a scalar.

For example,

We can write vectors in several ways,

Using an arrow
Using boldface
Underlined

\overrightarrow{AB} =\textbf{a}=\underline{a}

What are vector problems?

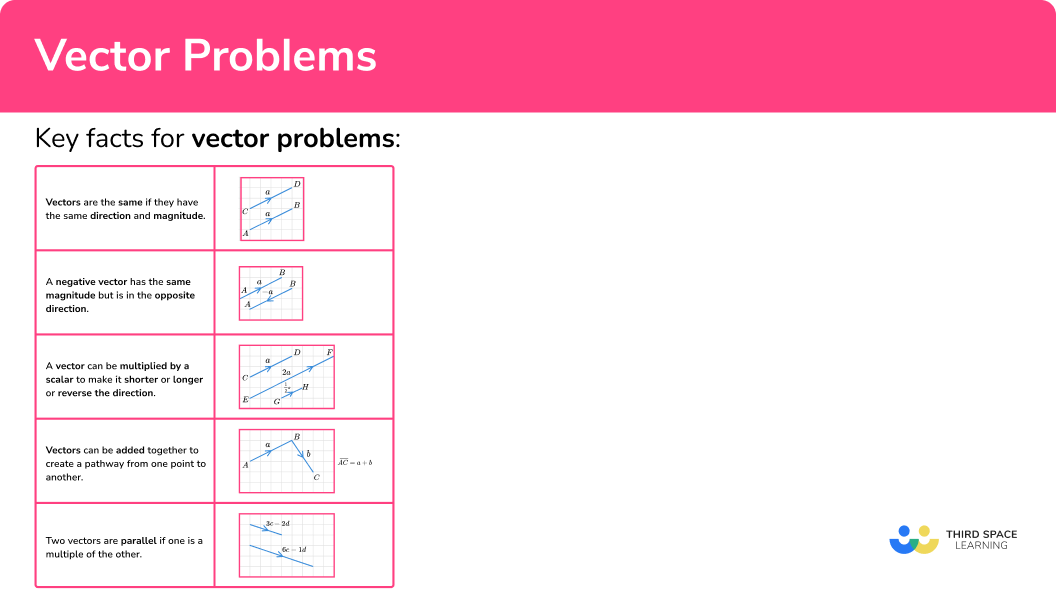
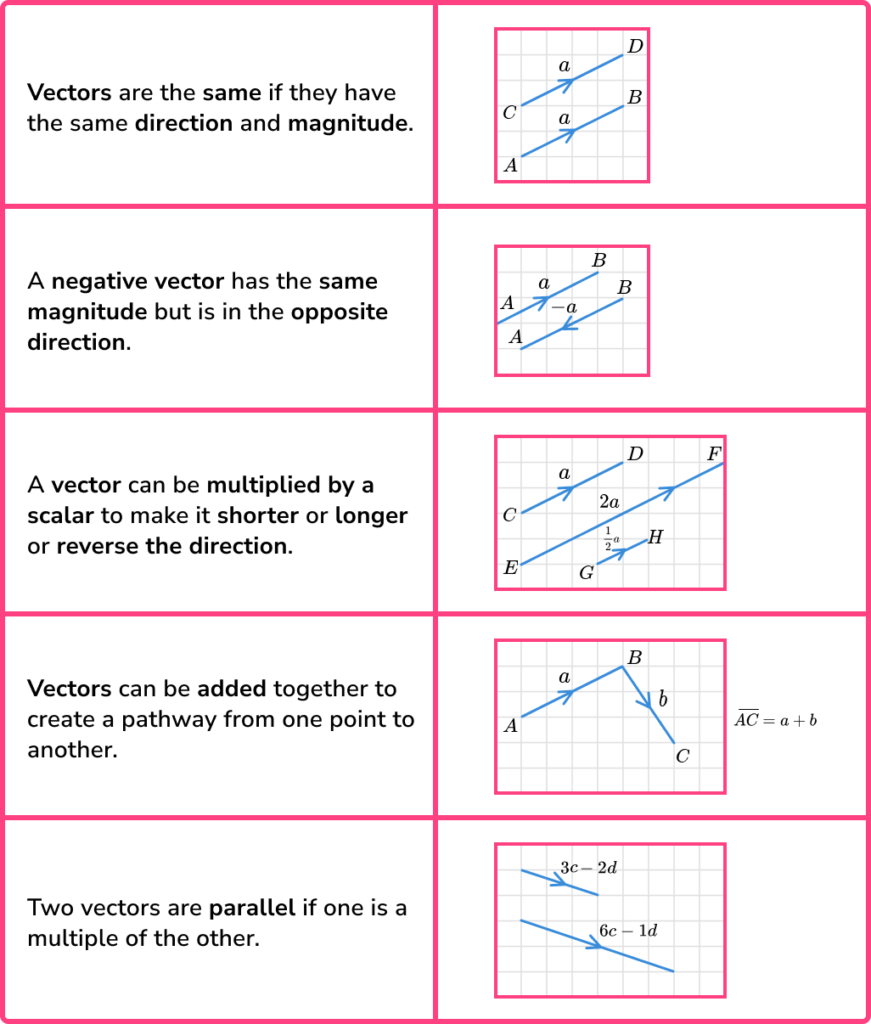
Key facts for vector problems

In order to solve problems involving vectors it is helpful to use several key facts.

How to solve vector problems

In order to solve vector problems:

Write any information you know onto the diagram.
Decide the route.
Write the vector.
Simplify your answer.

Explain how to solve vector problems

Vector problems worksheet

Get your free vector problems worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Vector problems worksheet

Get your free vector problems worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on vectors

Vector problems is part of our series of lessons to support revision on vectors. You may find it helpful to start with the main vectors lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Vector problem examples

Example 1: parallel lines

The shape below is made from $8$ equilateral triangles.

\overrightarrow{PQ} = \textbf{a},~ \overrightarrow{OQ} = \textbf{b}

Find the vector $\overrightarrow{QT}$ .

Write any information you know onto the diagram.

Parallel vectors of the same magnitude are the same. These triangles are all identical therefore we can label the corresponding vectors $a$ and $b$ .

2Decide the route.

We need to find a route where we know the vectors.

3Write the vector.

\overrightarrow{QT}=-\textbf{b}-\textbf{b}+\textbf{a}-\textbf{b}

4Simplify your answer.

\overrightarrow{QT}=\textbf{a}-3\textbf{b}

Example 2: extended line

\overrightarrow{AC}=\textbf{a}, ~\overrightarrow{BC}=\textbf{b}

The line $AB$ is extended to the point $D$ so that the length $AD$ is three times the length $AB$ .

Find the vector $\overrightarrow{AD}$ .

Write any information you know onto the diagram.

There is currently no further information we can add to the diagram.

Decide the route.

We know $AD$ is three times the length of $AB$ . We need to find a route from $A$ to $B$ and then multiply it by three.

Write the vector.

\overrightarrow{AB}=\textbf{a}-\textbf{b}\\\overrightarrow{AD}=3\overrightarrow{AB}=3(\textbf{a}-\textbf{b})

Simplify your answer.

\overrightarrow{AD}=3\textbf{a}-3\textbf{b}

Example 3: midpoint

\overrightarrow{BC} = \textbf{p}, ~\overrightarrow{BA}=\textbf{q}

$D$ is the midpoint of $AC$ . Find the vector $\overrightarrow{BD}$ .

Write any information you know onto the diagram.

When we are given information about midpoints, fractions of lines or ratios, it can be helpful to add this information onto the diagram. Here we are going to use the fraction $\frac{1}{2}$ to show that $D$ is half way along the line.

Decide the route.

We are trying to find a route from $B$ to $D$ . We know that $\overrightarrow{BC}=\textbf{p}$ and we then need to get from $C$ to $D$ . We also know that $CD=\frac{1}{2}CA$ .

We can find the vector $\overrightarrow{CA}$ and then half it.

$\begin{aligned} &\overrightarrow{CA}=-\textbf{p}+\textbf{q}\\\\ &\overrightarrow{CD}=\frac{1}{2}\overrightarrow{CA}=\frac{1}{2}(-\textbf{p}+\textbf{q}) \end{aligned}$

Now we have a route from $B$ to $D$ .

Write the vector.

\overrightarrow{BD}=\textbf{p}+\frac{1}{2}(-\textbf{p}+\textbf{q})

Simplify your answer.

\begin{aligned} &\overrightarrow{BD}=\textbf{p}+\frac{1}{2}(-\textbf{p}+\textbf{q})\\\\ &\overrightarrow{BD}=\textbf{p}-\frac{1}{2}\textbf{p}+\frac{1}{2}\textbf{q}\\\\ &\overrightarrow{BD}=\frac{1}{2}\textbf{p}+\frac{1}{2}\textbf{q} \end{aligned}

Example 4: fraction of a line

\begin{aligned} &\overrightarrow{AB} = 2\textbf{a}, ~ \overrightarrow{AC} =6\textbf{b}\\\\ &\text{BM }=\frac{1}{4}\text{ BA}, \text{ AN} = \frac{1}{3} \text{ AC} \end{aligned}

Find the vector $\overrightarrow{MN}$ .

Write any information you know onto the diagram.

When we are given information about midpoints, fractions of lines or ratios, it can be helpful to add this information onto the diagram. Here we know

$\text{BM }=\frac{1}{4}\text{ BA}, \text{ AN} = \frac{1}{3} \text{ AC}$ .

Decide the route.

We need to find a route from $M$ to $N$ . We can see that

$\text{MA}=\frac{3}{4}\text{BA and AN}=\frac{1}{3}\text{AC}$ .

$\overrightarrow{MA}=\frac{3}{4}\overrightarrow{BA}=\frac{3}{4}(-2\textbf{a})=-\frac{3}{2}\textbf{a}\\\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}=\frac{1}{3}(6\textbf{b})=2\textbf{b}$

We now have a route from $M$ to $N$ .

Write the vector.

\overrightarrow{MN}=-\frac{3}{2}\textbf{a}+2\textbf{b}

Simplify your answer.

The answer here cannot be simplified.

Example 5: ratio

\overrightarrow{FG} =\textbf{a}, ~ \overrightarrow{EH} =2\textbf{a}, ~ \overrightarrow{EF} =\textbf{b}

$ED =2EH$ and the point $J$ is such that $GJ:JH = 2:1$ .

Find the vector $\overrightarrow{JD}$ .

Write any information you know onto the diagram.

When we are given information about midpoints, fractions of lines or ratios, it can be helpful to add this information onto the diagram. Here we know $GJ:JH=2:1$ . This means that $\text{GJ}=\frac{2}{3}\text{GH and JH}=\frac{1}{3}\text{GH}$ .

We also know that $ED=2EH$ therefore $HD$ is the same length as $EH$ and in the same direction.

Decide the route.

We know $\text{JH}=\frac{1}{3}\text{GH}$ .

We can find the vector $\overrightarrow{GH}$ .

$\begin{aligned} &\overrightarrow{GH}=-\textbf{a}-\textbf{b}+2\textbf{a}=\textbf{a}-\textbf{b}\\\\ &\overrightarrow{JH}=\frac{1}{3}\overrightarrow{GH}=\frac{1}{3}(\textbf{a}-\textbf{b}) \end{aligned}$

We now have a route from $J$ to $D$ .

Write the vector.

\overrightarrow{JD}=\frac{1}{3}(\textbf{a}-\textbf{b})+2\textbf{a}

Simplify your answer.

\begin{aligned} &\overrightarrow{JD}=\frac{1}{3}(\textbf{a}-\textbf{b})+2\textbf{a}\\\\ &\overrightarrow{JD}=\frac{1}{3}\textbf{a}-\frac{1}{3}\textbf{b}+2\textbf{a}\\\\ &\overrightarrow{JD}=\frac{7}{3}\textbf{a}-\frac{1}{3}\textbf{b} \end{aligned}

Example 6: mix of information

\overrightarrow{AB} =6\textbf{a}, ~ \overrightarrow{BC} =10\textbf{b}

$E$ is the point on $AB$ such that $\text{EB }=\frac{1}{3}\text{ AB}$ .

$D$ is the point on $BC$ such that $CD:DB=1:4$ .

$F$ is the midpoint of $ED$ .

Find the vector $\overrightarrow{EF}$ .

Write any information you know onto the diagram.

Decide the route.

We want to find the the vector $\overrightarrow{EF}$ .

We know that $\text{EF}=\frac{1}{2}\text{ED}$ so we can start by finding the vector $\overrightarrow{ED}$ .

$\begin{aligned} &\overrightarrow{EB}=\frac{1}{3}\overrightarrow{AB}=\frac{1}{3}(6\textbf{a})=2\textbf{a}\\\\ &\overrightarrow{BD}=\frac{4}{5}\overrightarrow{BC}=\frac{4}{5}(10\textbf{b})=8\textbf{b} \end{aligned}$

$\overrightarrow{ED}=2\textbf{a}+8\textbf{b}$

Write the vector.

\overrightarrow{EF}=\frac{1}{2}\overrightarrow{ED}=\frac{1}{2} (2\textbf{a}+8\textbf{b})=\textbf{a}+4\textbf{b}

Simplify your answer.

This answer cannot be simplified.

How to show two vectors are parallel

Two vectors are parallel if one is a multiple of the other. This is because if one vector is a multiple of another, it is a bigger or smaller version of the other.

In order to show two vectors are parallel:

Work out each vector.
Show that one is a multiple of the other by factorising.

Showing two vectors are parallel examples

Example 7: two lines are parallel

Show that $AB$ is parallel to $CD$ .

Work out each vector.

\overrightarrow{CD}=\textbf{a}+2\textbf{b}

We need to find the vector $\overrightarrow{AB}$ .

$\begin{aligned} &\overrightarrow{AB}=4\textbf{a}+\textbf{a}+2\textbf{b}-3\textbf{a}+2\textbf{b}\\\\ &\overrightarrow{AB}=2\textbf{a}+4\textbf{b} \end{aligned}$

Show that one is a multiple of the other by factorising.

\overrightarrow{AB}=2\textbf{a}+4\textbf{b}=2(\textbf{a}+2\textbf{b})=2\overrightarrow{CD}

Since the vector $\overrightarrow{AB}$ is a multiple of the vector $\overrightarrow{CD}$ these vectors are parallel.

Example 8: two line segments form one straight line

$ABCD$ is a parallelogram.

The line $AB$ is extended to the point $E$ such that $\text{BE}=\frac{2}{3}\text{AB}$ .

The point $F$ is on the line $BC$ such that $BF:FC=2:3$ .

\overrightarrow{AB}=6\textbf{a}, \overrightarrow{CB}=5\textbf{b}

Show that $DFE$ is a straight line.

Work out each vector.

We need to find the vectors $\overrightarrow{DF} \text{ and } \overrightarrow{FE}$ .

$\begin{aligned} &\overrightarrow{CF}=\frac{3}{5}\overrightarrow{CB}=3\textbf{b}\\\\ &\overrightarrow{FB}=\frac{2}{5}\overrightarrow{CB}=2\textbf{b} \end{aligned}$

$\begin{aligned} &\overrightarrow{DF}=6\textbf{a}+3\textbf{b}\\\\ &\overrightarrow{FE}=4\textbf{a}+2\textbf{b} \end{aligned}$

Show that one is a multiple of the other by factorising.

\[\overrightarrow{\mathrm{DF}}=1.5(4 \mathbf{a}+2 \mathbf{b})=1.5 \overrightarrow{\mathrm{FE}}\]

Since $\overrightarrow{DF}$ is a multiple of $\overrightarrow{FE}$ the vectors are parallel. They also share the point $F$ meaning they form a straight line.

Common misconceptions

Using the wrong sign

Remember to make the vector negative when going backwards along it.

Mistakes with ratios

If two parts of a line are in the ratio 1:4, this means one part is ⅕ of a line and the other part ⅘ .

Practice vector problem questions

-\textbf{p}+3\textbf{q}

-\textbf{p}+\textbf{q}

-\textbf{p}+2\textbf{q}

\textbf{p}+2\textbf{q}

\overrightarrow{CE}=-\textbf{p}+2\textbf{q}

-2\textbf{a}+1.5\textbf{b}

-4\textbf{a}+3\textbf{b}

-2\textbf{a}+3\textbf{b}

2\textbf{a}-1.5\textbf{b}

\text{RM}=\frac{1}{2}\text{RQ}

\begin{aligned} &\overrightarrow{RQ}=-4\textbf{a}+3\textbf{b}\\\\ &\overrightarrow{RM}=\frac{1}{2}\overrightarrow{RQ}=\frac{1}{2}(-4\textbf{a}+3\textbf{b})=-2\textbf{a}+1.5\textbf{b} \end{aligned}

\frac{14}{3}\textbf{a}-\textbf{b}

\frac{10}{3}\textbf{a}+\textbf{b}

\textbf{b}+\frac{2}{3}\textbf{a}

\textbf{b}-\frac{2}{3}\textbf{a}

We know $\text{DC}=\frac{1}{3}\text{DC}$ so we need to find the vector $\overrightarrow{DC}$ .

\begin{aligned} &\overrightarrow{DC}=-4\textbf{a}+3\textbf{b}+2\textbf{a}=3\textbf{b}-2\textbf{a}\\\\ &\overrightarrow{DE}=\frac{1}{3}\overrightarrow{DC}=\frac{1}{3}(3\textbf{b}-2\textbf{a}) \end{aligned}

\begin{aligned} &\overrightarrow{AE}=4\textbf{a}+\frac{1}{3}(3\textbf{b}-2\textbf{a})\\\\ &\overrightarrow{AE}=4\textbf{a}+\textbf{b}-\frac{2}{3}\textbf{a}\\\\ &\overrightarrow{AE}=\frac{10}{3}\textbf{a}+\textbf{b} \end{aligned}

\frac{3}{2}\textbf{a}+2\textbf{b}

\frac{3}{2}\textbf{a}+\frac{4}{3}\textbf{b}

-\frac{3}{2}\textbf{a}-2\textbf{b}

\frac{3}{2}\textbf{a}-2\textbf{b}

We need to find a route from $P$ to $M$ . We can see $\overrightarrow{PB}=6\textbf{b}$ .

We know that $BM=\frac{1}{2}BN$ so we need to find the vector $\overrightarrow{BN}$ .

\begin{aligned} &\overrightarrow{BN}=-8\textbf{b}+3\textbf{a}\\\\ &\overrightarrow{BM}=\frac{1}{2}\overrightarrow{BN}=\frac{1}{2}(-8\textbf{b}+3\textbf{a})\\\\ &\overrightarrow{PM}=6\textbf{b}+\frac{1}{2}(-8\textbf{b}+3\textbf{a})\\\\ &\overrightarrow{PM}=6\textbf{b}-4\textbf{b}+\frac{3}{2}\textbf{a}\\\\ &\overrightarrow{PM}=\frac{3}{2}\textbf{a}+2\textbf{b} \end{aligned}

\frac{5}{2}\textbf{a}+4\textbf{b}

\textbf{a}-4\textbf{b}

\frac{5}{8}\textbf{a}+\textbf{b}

-\frac{5}{4}\textbf{a}-\frac{23}{4}\textbf{b}

We need to begin by finding the vector $\overrightarrow{AD}$ .

\begin{aligned} &\overrightarrow{AB}=2\textbf{a}+6\textbf{b}\\\\ &\overrightarrow{BC}=-2\textbf{a}-6\textbf{b}+3\textbf{a}+2\textbf{b}=\textbf{a}-4\textbf{b}\\\\ &\overrightarrow{BD}=\frac{1}{2}\overrightarrow{BC}=\frac{1}{2}\textbf{a}-2\textbf{b}\\\\ &\overrightarrow{AD}=2\textbf{a}+6\textbf{b}+\frac{1}{2}\textbf{a}-2\textbf{b}=\frac{5}{2}\textbf{a}+4\textbf{b}\\\\ &\overrightarrow{AE}=\frac{1}{4}(\frac{5}{2}\textbf{a}+4\textbf{b})=\frac{5}{8}\textbf{a}+\textbf{b} \end{aligned}

\overrightarrow{AB}

\overrightarrow{AC}

\overrightarrow{CE}

\overrightarrow{BE}

\begin{aligned} &\overrightarrow{AB}=4\textbf{a}\\\\ &\overrightarrow{AC}=4\textbf{a}+4\textbf{b}\\\\ &\overrightarrow{CE}=4\textbf{b}-4\textbf{a}\\\\ &\overrightarrow{BE}=8\textbf{b}-4\textbf{a} \end{aligned}

$4\textbf{b}-4\textbf{a}=4(\textbf{b}-\textbf{a})$ so $\overrightarrow{CE}$ is parallel to $\textbf{b}-\textbf{a}$ .

Vector problems GCSE questions

1. $\overrightarrow{AB}=6\textbf{b},\overrightarrow{BC}=9\textbf{a},\overrightarrow{DF}=-3\textbf{a}+3\textbf{b}$

$F$ is the midpoint of $AB$ . Show that $AD$ is parallel to $BC$ .

(2 marks)

Show answer

\overrightarrow{AD}=3\textbf{b}-(-3\textbf{a}+3\textbf{b})=3\textbf{a}

(1)

$\overrightarrow{BC} =3\overrightarrow{AD}$ – they are multiples of each other therefore parallel.

(1)

2. $\overrightarrow{AD}=12\textbf{a}, \overrightarrow{CD}=8\textbf{b}$

AD=1.5BC.

$E$ is the midpoint of $AB$ .

EF:FC=1:3.

Find the vector $\overrightarrow{BF}$ .

(4 marks)

Show answer

\overrightarrow{BC}=8\textbf{a}

(1)

\overrightarrow{EB}=\frac{1}{2}(12\textbf{a}-8\textbf{b}-8\textbf{a})=2\textbf{a}-4\textbf{b}

(1)

\overrightarrow{EC}=2\textbf{a}-4\textbf{b}+8\textbf{a}=10\textbf{a}-4\textbf{b}

(1)

\overrightarrow{EF}=\frac{1}{4}(10\textbf{a}-4\textbf{b})=\frac{5}{2}\textbf{a}-\textbf{b}

(1)

3. $\overrightarrow{AB}=4\textbf{a}, \overrightarrow{BC}=2\textbf{b}$

$D$ is the midpoint of $AB.$

Point $E$ is such that $AE:EC=3:1$ .

BF=2BC.

Determine whether $DEF$ is a straight line.

(4 marks)

Show answer

\overrightarrow{CE}=\frac{1}{4}(-2\textbf{b}-4\textbf{a})=-\frac{1}{2}\textbf{b}-\textbf{a}

(1)

\overrightarrow{DE}=2\textbf{a}+2\textbf{b}-\frac{1}{2}\textbf{b}-\textbf{a}=\textbf{a}+\frac{3}{2}\textbf{b}

(1)

\overrightarrow{EF}=\frac{1}{2}\textbf{b}+\textbf{a}+2\textbf{b}=\textbf{a}+\frac{5}{2}\textbf{b}

(1)

$DEF$ is not a straight line since $\overrightarrow{DE}$ and $\overrightarrow{EF}$ and are not multiples of each other and therefore are not parallel.

(1)

Learning checklist

You have now learned how to:

Solve complex problems involving vectors

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.