Symmetry

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

Coordinates Straight line graphs Parallel and perpendicular lines Types of graphs

This topic is relevant for:

GCSE Maths Geometry and Measure 2D Shapes

Symmetry

Here we will learn about symmetry, including line and rotational symmetry properties within polygons, angle properties, and symmetry of different line graphs.

There are also symmetry worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is symmetry?

Symmetry is when a line is drawn through a shape to make one side of the line a reflection of the other. It is a property of a 2D polygon or 3D polyhedron.

There are two different types of symmetry that you need to be aware of: lines of symmetry and rotational symmetry.

Although the two sound similar, they are fundamentally different.

What is symmetry?

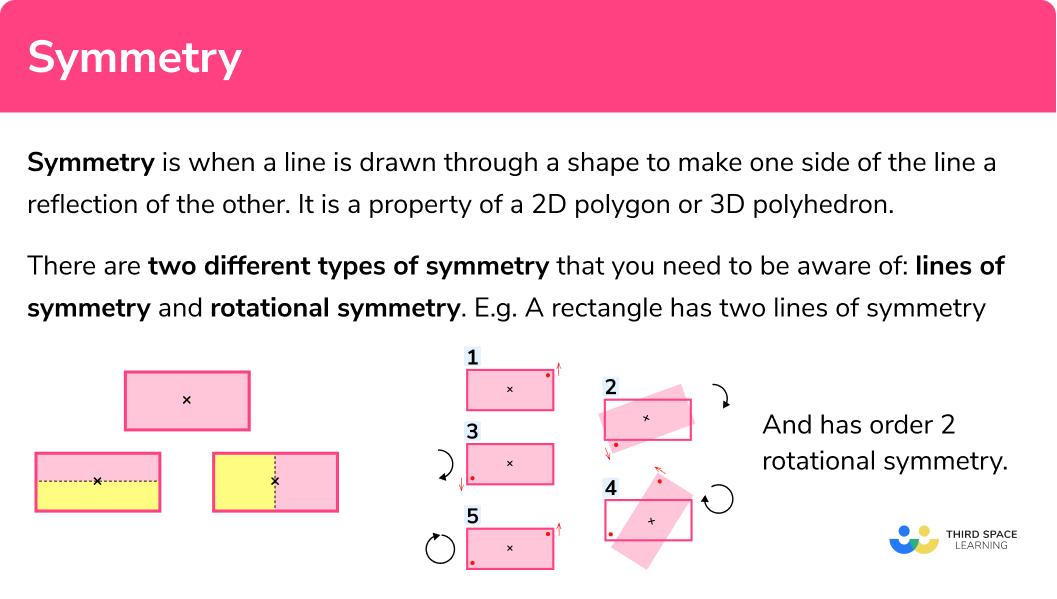
Lines of symmetry

The number of lines of symmetry for a shape can be determined by using a ruler to visualise when the polygon can be divided equally into 2 equal pieces that are a reflection of each other.

E.g.

How many lines of symmetry does a rectangle have?

Here, the pink and yellow sections are congruent to each other and are symmetrical to each other.

The number of lines of symmetry for any rectangle (excluding a square, which is a special rectangle), is $2$ .

Step-by-step guide: Lines of symmetry

Rotational symmetry

The rotational symmetry of a shape is worked out using the centre of the polygon. We need to determine where the centre of the polygon is using the diagonals as they intersect at the centre of the shape. Once we know the centre, we need to rotate the polygon around its centre to determine the order of rotation.

Tracing paper is very useful to determine the order of rotation of a polygon because you can trace the shape and rotate the tracing around the centre, not affecting the original.

E.g.

What is the order of rotational symmetry of a rectangle?

After rotating the rectangle $180^o$ , the image is an exact copy of the original. After a further rotation of $180^o$ , we get back to the original orientation.

This means that the order of rotational symmetry for the rectangle (excluding a square, which is a special rectangle) is $2$ .

Step-by-step guide: Rotational symmetry

How to use symmetry

In order to draw lines of symmetry:

Locate the centre of the 2D shape.
Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.
Continue to rotate the ruler around $180$ degrees over the centre point to cover all sides and vertices.

In order to calculate the order of rotational symmetry:

Locate the centre of the 2D shape.
Trace the shape onto a piece of tracing paper including the centre and northline.
Rotate the tracing around the centre and count the number of identical occurrences.

Explain how to use symmetry

Symmetry worksheet

Get your free symmetry worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Symmetry worksheet

Get your free symmetry worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Symmetry examples

Example 1: the square (lines of symmetry)

Draw all of the lines of symmetry for the square below.

Locate the centre of the 2D shape.

Draw a small $x$ in the centre of the square (this does not have to be exact)

2Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.

Here we can draw a vertical line as this divides the shape into two identical rectangles (one is a reflection of the other), and a horizontal line as this divides the shape into two congruent rectangles that are a reflection of each other.

3Continue to rotate the ruler around $180$ degrees over the centre point to cover all sides and vertices.

As the shape has an even number of vertices, we can pass through opposing vertices to see whether there is a line of symmetry present. For the square, we can draw a further two lines of symmetry (along the diagonals of the square).

The square has $4$ lines of symmetry.

Example 2: using angles (lines of symmetry)

Show that the hexagon below has no lines of symmetry.

Locate the centre of the 2D shape.

Draw a small $x$ in the centre of the hexagon (this does not have to be exact)

Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.

Imagine drawing a line from A to D. If this is a line of symmetry then the angles B and F, and C and E must be equal to one another. As C and E are not equal to each other, the line AD is not a line of symmetry.

Continue to rotate the ruler around $180$ degrees over the centre point to cover all sides and vertices.

As the shape has an even number of vertices, we need to pass through opposite vertices and then pass through opposing sides. When we pass through opposing vertices, we get:

When we pass through opposing sides, we get:

As there is no line that can be drawn through opposing vertices or sides of the shape that splits the shape into two reflected parts, this shape has no lines of symmetry.

Example 3: quadratic graph (lines of symmetry)

Write the equation of the line of symmetry for the quadratic equation $y=x^2-8x+12$ .

Locate the centre of the 2D shape.

Here, rather than locating the centre, we are going to locate the turning point of the curve. The turning point is the point on the curve where the gradient changes from positive to negative, or vice versa.

For the graph of $y=x^2-8x+12$ , we can see that the turning point is at $(4,-4)$ however for questions without a visual representation, the turning point can be calculated by completing the square:

$\begin{aligned} &y=(x-4)^2-16+12\\\\ &y=(x-4)^2-4 \end{aligned}$

Turning Point: $(4,-4)$ .

Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.

Here we can see that if we sketch a vertical line through the turning point $(4,-4)$ , the coordinates on either side of this line are the same distance away from the line. This means that the vertical line that intersects the $x$ axis at $4$ is a line of symmetry, or $x=4$ .

Continue to rotate the ruler around $180$ degrees over the centre point to cover all sides and vertices.

By rotating the ruler around the turning point, there are no other lines that show a symmetry in the graph of $y=x^2-8x+12$ . The only line of symmetry therefore is $x=4$ .

Example 4: the regular hexagon (rotational symmetry)

Calculate the order of rotational symmetry for a regular pentagon.

Locate the centre of the 2D shape.

Draw a small $x$ in the centre of the hexagon (join the opposing vertices together to locate the centre)

Trace the shape onto a piece of tracing paper including the centre and northline.

As the regular pentagon has a lot of vertices, it is useful to also draw a dot in one vertex so you don’t lose sight of what the original looks like:

Rotate the tracing around the centre and count the number of identical occurrences.

Rotating the shape around the centre, there are multiple occasions when the shape is identical to the original. Below we have shown multiple stages of the rotation:

By placing a dot in each position when the shape is identical, we can count the order of rotation once the shape has been rotated $360^o$ around the centre.

The regular pentagon has a rotational symmetry of order $5$ .

Example 5: angle facts (rotational symmetry)

The rhombus ABCD has two pairs of parallel sides. Use angle facts to calculate the order of rotation for the shape ABCD.

Locate the centre of the 2D shape.

To find the centre of the shape, join the diagonals together. Here we have:

Next we need to calculate all of the interior angles of the shape and use them to calculate the order of rotation:

BCD $= 180-62 = 118^o$ (angles on a straight line total $180^o$ )

ABC $= 62^o$ (alternate angles are equal)

BAD $= 180-62 = 118^o$ (co-interior angles total $180^o$ )

ADC $= 180-118 = 62^o$ (co-interior angles total $180^o$ ).

We now have the following information:

Trace the shape onto a piece of tracing paper including the centre and northline.

Again, we are going to try visualising the rotation without tracing paper by rotating the polygon $360^o$ around its centre.

Rotate the tracing around the centre and count the number of identical occurrences.

There are two occurrences when the image matches the original and so the order of rotation for the rhombus ABCD is $2$ .

Example 6: cubic graph (rotational symmetry)

Calculate the order of rotational symmetry for the cubic graph $y=x^3+2$ around the centre $(0,0)$ .

Locate the centre of the 2D shape.

We know the centre $(0,0)$ so let us draw it onto the graph:

Trace the shape onto a piece of tracing paper including the centre and northline.

As the shape is now a graph, sketch the graph onto a piece of tracing paper. You do not need to include the axes as it is the graph that is important.

Rotate the tracing around the centre and count the number of identical occurrences.

If we turn the tracing $180^o$ around the point $(0,0)$ we get a match with the original. This is the only occurrence along with the original and so the order of rotation for the cubic graph $y=-0.1x^3$ around the point $(0,0)$ is $2$ .

Common misconceptions

Rotational symmetry/lines of symmetry

Lines of symmetry are mixed up with rotational symmetry. A line of symmetry divides the shape equally into two symmetrical pieces. A rotational symmetry is the number of times a shape fits into itself when rotated around its centre.

The diagonals of quadrilaterals

The diagonals of a quadrilateral are joined together and highlighted as a line of symmetry. The only quadrilateral where this is true is the square. Below is the example for an incorrect line of symmetry for a rectangle.

The number of sides = the number of lines of symmetry

Although this is true for regular shapes, this is not true for all shapes.

Rotational symmetry of order $\pmb{0}$

A shape that has an order of rotational symmetry of $1$ can also be said to have an order of $0$ , but 1 or “no rotational symmetry” are better descriptions.

The number of sides = the order of rotational symmetry

Although this is true for regular shapes, this is not true for all shapes.

Practice lines of symmetry questions

5

1

0

2

Practice lines of symmetry question 1 explanation 1

0

1

2

3

Practice lines of symmetry question 2 explanation 1

y=3

y=3x

x=3

y=x+3

Practice lines of symmetry question 3 explanation 1

0

1

2

4

Practice lines of symmetry question 4 explanation 1

1

2

3

4

Practice lines of symmetry question 5 explanation 1

0

1

2

4

Practice lines of symmetry question 6 explanation 1

When rotated $180^o$ , the image is the same as the original.

Symmetry GCSE questions

1. Complete the table to state the order of rotation for the following shapes

Shape Order of Rotation

Square

Isosceles Triangle

Parallelogram

Regular Octagon

(4 marks)

Show answer

Shape Order of Rotation

Square $\hspace{3cm} 4$

Isosceles Triangle $\hspace{1.6cm} 0 or 1$

Parallelogram $\hspace{2.1cm} 2$

Regular Octagon $\hspace{1.7cm} 8$

(4)

2. (a) Complete table of values for the cubic $y=x^3.$

\begin{aligned} &x \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad 2 \quad \quad \quad 3 \\ &y \quad \quad \quad \quad \quad \;\; -1 \quad \quad \quad 0 \quad \quad \quad 1 \end{aligned}

(b) James says “the graph of $y=x^3$ has a line of symmetry at $x=0.$ ” Is he correct? Explain your answer.

(6 marks)

Show answer

(a)

\begin{aligned} &x \quad \quad -2 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad 2 \quad \quad \quad 3 \\ &y \quad \quad -8 \quad \quad -1 \quad \quad \quad 0 \quad \quad \quad 1 \quad \quad \quad 8 \quad \quad \quad 27 \end{aligned}

(1)

(b)

(1)

$y$ is positive when $x>0$ and y is negative when $x<0$ so they are not symmetrical

(1)

(c)

2

(1)

3. Calculate the equation of the line of symmetry for the line $y=4x+1$ at the point $(4,17).$

(3 marks)

Show answer

Perpendicular gradient $m=-0.25$

(1)

$y=-0.25x+c$ at $(2,9)$ means $17=-0.25 \times 4+c, \; c=18$

(1)

$y=-0.25x+18$

(1)

Learning checklist

You have now learned how to:

Identify lines of symmetry in 2-D shapes presented in different orientations

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.