Iteration maths

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

In order to access this I need to be confident with:

BIDMAS Calculator skills Rearranging equations Nth term Sequences Substitution Compound interest Solving equations Algebraic fractions

This topic is relevant for:

GCSE Maths Algebra Equations Solving Equations

Iteration Maths

Here we will learn about iteration, including how to find approximate solutions to equations using iterative methods and work with general iterative processes to set up and solve problems.

There are also iteration worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is iteration?

Iteration is a repeated mathematical process that allows us to find approximate solutions for equations.

To do this we need to know the iterative formula and the starting value.

The iterative formula tells us how to find the next solution, which we label as $x_{n+1},$ given the current solution, which we label as $x_{n}.$

The iterative formula changes for every equation and using a different starting number can greatly affect the values of the solutions. We usually label the starting number as $x_{0}.$

For example,

The iterative formula to determine the next integer is

x_{n+1}=x_{n}+1.

If we know that $x_{0}=3$ and we want to calculate the value of $x_{1},$ we would substitute this into the iterative formula above with $n=0$ (as $x_{n=0}=x_{0}=3)$ to get

\begin{aligned} x_{0+1}&=x_{0}+1\\\\ x_{1}&=3+1=4 \end{aligned}

So $x_{1}=4.$

This iterative formula will always find the next integer in a sequence for any value of $n.$

What is iteration?

Iteration and sequences

Iteration generates a sequence of numbers.

If the sequence tends towards a specific number (which is the approximate solution) then this is known as a converging sequence (or convergent sequence).

For example,

$x_{n+1}=\frac{x_{n}}{10}$ converges towards $0$ when $x_{n}$ ≠ $0.$

This is because each subsequent solution is the previous solution divided by $10$ and so each number in the sequence would be $10$ times smaller than the previous value.

However, if $x_{n}=0$ then we get a sequence of zeros as we repeat the calculation $0\div{10}=0.$

If the sequence does not tend towards a specific number, moreover the values become much more extreme, this is known as a diverging sequence (or divergent sequence).

For example,

$x_{n+1}=3x_{n}$ is a diverging sequence when $x_{n}$ ≠ $0.$

This is because each subsequent solution is three times larger than the previous solution but if $x_{n}=0$ then we get a sequence of zeros as we repeat the calculation $3\times{0}=0.$

If the iteration cycles between one or more numbers, this is known as an oscillating sequence.

For example,

$x_{n+1}=\frac{1}{x_{n}}$ oscillates between two numbers or is always equal to $1.$

This is because, if we are continuously calculating the reciprocal of the previous value, the reciprocal of the reciprocal of a number is the original value (the reciprocal of $2$ is $\frac{1}{2},$ and the reciprocal of $\frac{1}{2}$ is $2$ ) and so if $x_{0}=2,$ we would generate the iterative sequence.

2, \ \frac{1}{2}, \ 2, \ \frac{1}{2}, \ 2, \ \frac{1}{2}, \ 2, \ \frac{1}{2},\ldots

If $x_{0}=1,$ the reciprocal of $1$ is $1$ and so we would get the sequence $1, 1, 1, 1, 1,\ldots.$

When we are finding an approximate solution to an equation using iteration, we are looking for a converging sequence. We can only approximate one solution using the value of $x_{n}.$ To approximate another would require a different value for $x_{n}.$

Also, it is not always the case that when $x_{n}=0$ the sequence of values for the solutions oscillate. This is due to the specific nature of the iterative formula.

Solutions may be irrational numbers. Make sure that you do not round any value you are calculating with, only round your solution. For this reason, you may need to use a calculator to complete the iteration.

How to use iteration

In order to use iteration to find an approximate solution to an equation:

Substitute $x_{n}$ into the iteration formula.
Calculate the solution for $x_{n+1}$ .
Repeat by substituting $x_{n+1}$ into the iteration formula until the required approximation is reached.

Explain how to use iteration

Iteration maths worksheet

Get your free iteration maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Iteration maths worksheet

Get your free iteration maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on solving equations

Iteration maths is part of our series of lessons to support revision on solving equations. You may find it helpful to start with the main solving equations lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Iteration maths examples

Example 1: iteration (diverging sequence)

Calculate the value of $x_{3}$ for the iterative formula $x_{n+1}=x_{n}+2$ with $x_{0}=1.$

Substitute $x_{n}$ into the iteration formula.

To calculate the value of $x_{3},$ we need to calculate the value of $x_{1}$ and $x_{2}$ first. As $x_{0}=1,$ this means that $n=0$ and so substituting these values into the iteration formula, we have

\begin{aligned} x_{0+1}&=x_{0}+2\\\\ x_{1}&=1+2 \end{aligned}

2Calculate the solution for $x_{n+1}$ .

Calculating the value of $x_{1}$ we now have $x_{1}=3.$

3Repeat by substituting $x_{n+1}$ into the iteration formula until the required approximation is reached.

Substituting $x_{1}=3$ into the iteration formula (now $n=1$ ), we have

\begin{aligned} x_{1+1}&=x_{1}+2\\\\ x_{2}&=3+2\\\\ x_{2}&=5 \end{aligned}

Substituting $x_{2}=5$ into the iteration formula (now $n=2$ ), we have

\begin{aligned} x_{2+1}&=x_{2}+2\\\\ x_{3}&=5+2\\\\ x_{3}&=7 \end{aligned}

The solution is $x_{3}=7.$

Example 2: iteration (converging sequence)

Calculate the value of $x_{2}$ for the iterative formula $x_{n+1}=\frac{x_{n}}{6}$ with $x_{0}=1296.$

Substitute $x_{n}$ into the iteration formula.

To calculate the value of $x_{2},$ we need to calculate the value of $x_{1}.$ As $x_{0}=1296,$ this means that $n=0$ and so substituting these values into the iteration formula, we have

$\begin{aligned} x_{0+1}&=\frac{x_{0}}{6}\\\\ x_{1}&=\frac{1296}{6} \end{aligned}$

Calculate the solution for $x_{n+1}$ .

Calculating the value of $x_{1}$ we now have $x_{1}=216.$

Repeat by substituting $x_{n+1}$ into the iteration formula until the required approximation is reached.

Substituting $x_{1}=216$ into the iteration formula (now $n=1$ ), we have

$\begin{aligned} x_{1+1}&=\frac{x_{1}}{6}\\\\ x_{2}&=\frac{216}{6}\\\\ x_{2}&=36 \end{aligned}$

The solution is $x_{2}=36.$

Example 3: iteration (negative value of x_₀)

Calculate the value of $x_{3}$ for the iterative formula $x_{n+1}=3x_{n}-5$ with $x_{0}=-2.$

Substitute $x_{n}$ into the iteration formula.

To calculate the value of $x_{3},$ we need to calculate the value of $x_{1}$ and $x_{2}.$ As $x_{0}=-2,$ this means that $n=0$ and so substituting these values into the iteration formula, we have

$\begin{aligned} x_{0+1}&=(3\times{x_{0}})-5\\\\ x_{1}&=(3\times{-2})-5 \end{aligned}$

Calculate the solution for $x_{n+1}$ .

Calculating the value of $x_{1}$ we have $x_{1}=-6-5=-11.$

Repeat by substituting $x_{n+1}$ into the iteration formula until the required approximation is reached.

Substituting $x_{1}=-11$ into the iteration formula (now $n=1$ ), we have

$\begin{aligned} x_{1+1}&=(3\times{x_{1}})-5\\\\ x_{2}&=(3\times{-11})-5\\\\ x_{2}&=-33-5\\\\ x_{2}&=-38 \end{aligned}$

Substituting $x_{2}=-38$ into the iteration formula (now $n=2$ ), we have

$\begin{aligned} x_{2+1}&=(3\times{x_{2}})-5\\\\ x_{3}&=(3\times{-38})-5\\\\ x_{3}&=-114-5\\\\ x_{3}&=-119 \end{aligned}$

The solution is $x_{3}=-119.$

Example 4: iteration including fractions

Calculate the value of $x_{1}, x_{2}$ and $x_{3}$ when $x_{n+1}=\frac{7}{x_{n}}+4$ and initial value $x_{0}=4.$

Substitute $x_{n}$ into the iteration formula.

We need to calculate the value of $x_{1}$ first. As $x_{0}=4,$ this means that $n=0$ and so substituting these values into the iteration formula, we have

$\begin{aligned} x_{0+1}&=\frac{7}{x_{0}}+4\\\\ x_{1}&=\frac{7}{4}+4 \end{aligned}$

Calculate the solution for $x_{n+1}$ .

Calculating the value of $x_{1}$ we have $x_{1}=\frac{23}{4}=5.75.$

Repeat by substituting $x_{n+1}$ into the iteration formula until the required approximation is reached.

Substituting $x_{1}=5.75$ into the iteration formula (now $n=1$ ), we have

$\begin{aligned} x_{1+1}&=\frac{7}{x_{1}}+4\\\\ x_{2}&=\frac{7}{5.75}+4\\\\ x_{2}&=\frac{120}{23}=5.217391304… \end{aligned}$

Substituting $x_{2}=\frac{120}{23}$ into the iteration formula (now $n=2$ ), we have

$\begin{aligned} x_{2+1}&=\frac{7}{x_{2}}+4\\\\ x_{3}&=7\div{\frac{120}{23}}+4\\\\ x_{3}&=7\times\frac{23}{120}+4\\\\ x_{3}&=\frac{161}{120}+4\\\\ x_{3}&=\frac{641}{120}=5.3341\dot{6} \end{aligned}$

The solution is $x_{1}=5.75, \ x_{2}=\frac{120}{23},$ and $x_{3}=\frac{641}{120}.$

Note, here we can write the fraction as the most precise answers for $x_{1}, \ x_{2},$ and $x_{3}.$

Example 5: iteration including powers

Calculate the value of $x_{3}$ when $x_{n+1}=3x_{n}^{2}$ and $x_{0}=\frac{1}{6}.$ Write your answer in standard form to a suitable degree of accuracy.

Substitute $x_{n}$ into the iteration formula.

We need to calculate the value of $x_{1}$ first. Substituting $x_{0}=\frac{1}{6}$ with $n=0$ into the iteration formula, we have

$\begin{aligned} x_{0+1}&=3\times{x^{2}_{0}}\\\\ x_{1}&=3\times\left(\frac{1}{6}\right)^{2} \end{aligned}$

Calculate the solution for $x_{n+1}$ .

Calculating the value of $x_{1}$ we have $x_{1}=3\times\frac{1}{36}=\frac{1}{12}.$

Repeat by substituting $x_{n+1}$ into the iteration formula until the required approximation is reached.

Substituting $x_{1}=\frac{1}{12}$ into the iteration formula (now $n=1$ ), we have

$\begin{aligned} x_{1+1}&=3\times\left(\frac{1}{12}\right)^{2}\\\\ x_{2}&=3\times\frac{1}{144}\\\\ x_{2}&=\frac{1}{48} \end{aligned}$

Substituting $x_{2}=\frac{1}{48}$ into the iteration formula (now $n=2$ ), we have

$\begin{aligned} x_{2+1}&=3\times\left(\frac{1}{48}\right)^{2}\\\\ x_{3}&=3\times\frac{1}{2304}\\\\ x_{3}&=\frac{1}{768}\\\\ x_{3}&=1.30\times{10}^{-3}\text{ (2dp)} \end{aligned}$

The solution is $x_{3}=1.30\times{10}^{-3} \ (2dp).$

Example 6: iteration including powers and fractions

Calculate the value of $x_{2}$ when $x_{n+1}=\frac{2}{x_{n}^{2}}-8$ and $x_{0}=0.4.$ Write your answer to $3$ decimal places.

Substitute $x_{n}$ into the iteration formula.

Substituting $x_{0}=0.4$ with $n=0$ into the iteration formula, we have

$\begin{aligned} x_{0+1}&=\frac{2}{x_{0}^{2}}-8\\\\ x_{1}&=\frac{2}{0.4^{2}}-8 \end{aligned}$

Calculate the solution for $x_{n+1}$ .

Calculating the value of $x_{1}$ we now have $x_{1}=\frac{2}{0.16}-8=4.5.$

Repeat by substituting $x_{n+1}$ into the iteration formula until the required approximation is reached.

Substituting $x_{1}=4.5$ into the iteration formula (now $n=1$ ), we have

$\begin{aligned} x_{1+1}&=\frac{2}{x_{1}^{2}}-8\\\\ x_{2}&=\frac{2}{4.5^{2}}-8\\\\ x_{2}&=\frac{8}{81}-8\\\\ x_{2}&=-\frac{640}{81} \end{aligned}$

Substituting $x_{2}=-\frac{640}{81}$ into the iteration formula (now $n=2$ ), we have

$\begin{aligned} x_{2+1}&=\frac{2}{x_{2}^{2}}-8\\\\ x_{3}&=\frac{2}{\left(\frac{640}{81}\right)^{2}}-8\\\\ x_{3}&=0.03203613281…-8\\\\ x_{3}&=-7.967963867… \end{aligned}$

The solution is $x_{3}=-7.968 \ (3dp).$

Generating the iteration formula for an equation

To generate the iteration formula for an equation, we need to be able to rearrange the equation so that the subject $x$ is also dependent on itself.

For example,

To explain the relationship between the quadratic equation $x^{2}+8x-20=0$ and the iterative formula $x_{n+1}=\frac{20}{x_{n}}-8$ we need to remove the labelling of $x_{n+1}$ and $x_{n}$ and rearrange this to get the quadratic.

Removing the labelling, we have

x=\frac{20}{x}-8.

Multiplying both sides of the equation by $x$ we have

x^{2}=20-8x.

Adding $8x$ to both sides of the equation, we have

x^{2}+8x=20.

Finally subtracting $20$ from both sides of the equation, we have

x^{2}+8x-20=0.

The iteration formula for an equation is a rearrangement of the equation, but we need to make sure that the variable $x$ occurs on both sides of the equals sign.

How to determine an iteration formula

In order to determine an iteration formula for an equation:

Rearrange the equation so that the highest power of $x$ is the subject.
Divide throughout by one less than the highest power of $x$ .
Rewrite using $x_n$ and $x_{n+1}$ .

Explain how to determine an iteration formula

Example 7: generating an iterative formula

Determine an iterative formula that will calculate an approximate solution for the equation $x^{3}-6x=0.$

Rearrange the equation so that the highest power of $x$ is the subject.

Adding $6x$ to both sides of the equation, we have

$x^{3}=6x.$

Divide throughout by one less than the highest power of $x$ .

Dividing both sides by $x^2$ we have

$x=\frac{6x}{x^2}=\frac{6}{x}.$

Rewrite using $x_n$ and $x_{n+1}$ .

As the next solution is dependent on the current solution, we can write the iterative formula

$x_{n+1}=\frac{6}{x_{n}}.$

Common misconceptions

Rounding too early

If you round the value for $x_1$ this will have an impact on the value of $x_2.$ It is therefore important to only round the solutions, and not use rounded numbers within any further calculation.

Incorrect labelling of solutions

When $n=0$ for $x_{n},$ the value of $x_{n+1}=x_{0+1}=x_1$ which is the next value in the sequence. This means that if we know the value of $x_{0},$ we can determine the value of $x_1$ (the next approximate solution).

Calculating the final approximate solution straight away

If you are given $x_0$ and you need to calculate the value of $x_3$ , students would incorrectly try to calculate $x_3$ straight away rather than calculating the values of $x_1$ and $x_2$ first. We can only calculate the next term in the sequence if we know the current term and the iterative formula.

$x_{n+1}$ is the same as $x_{n}+1$

The algebraic notation is misinterpreted as $1$ more than the value of $x_{n}$ whereas the label $n+1$ is the next value in the sequence. Moreover, $n$ is the current value in the sequence, and $n-1$ would be the previous value in the sequence.

Practice iteration maths questions

x_{3}=0

x_{3}=3

x_{3}=6

x_{3}=9

Iteration Maths practice question 1

x_{2}=-0.16

x_{2}=-0.4

x_{2}=-1

x_{2}=-2.5

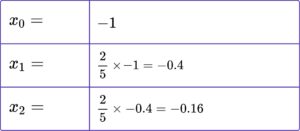
Iteration Maths practice question 2

x_{4}=-1

x_{4}=2

x_{4}=-7

x_{4}=17

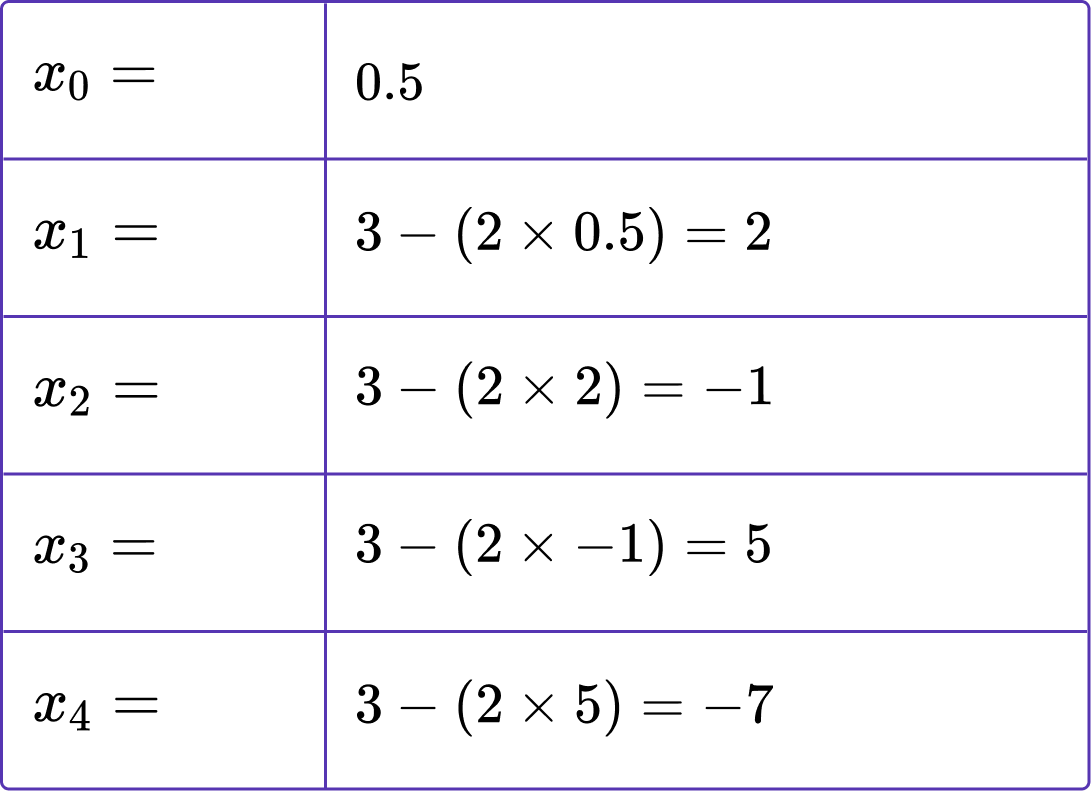
Iteration Maths practice question 3

x_{2}=5.250 \ (3dp)

x_{2}=5.694 \ (3dp)

x_{2}=5.702 \ (3dp)

x_{2}=5.762 \ (3dp)

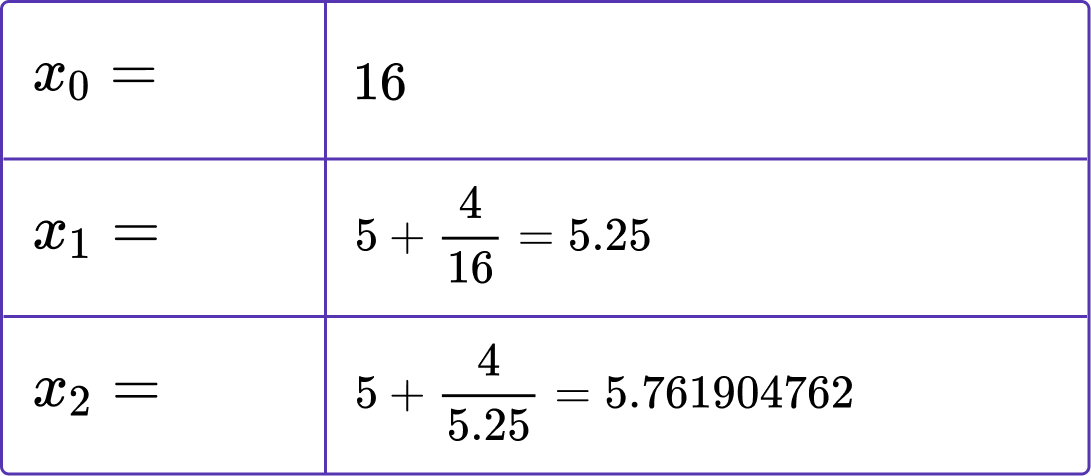
Iteration Maths practice question 4

x_{3}=2.2857 \ (4dp)

x_{3}=0.7464 \ (4dp)

x_{3}=0.0796 \ (4dp)

x_{3}=0.0009 \ (4dp)

Iteration Maths practice question 5

x_{4}=-44.1 \ (3dp)

x_{2}=-2.000 \ (3dp)

x_{4}=0.326 \ (3dp)

x_{4}=1.367 \ (3dp)

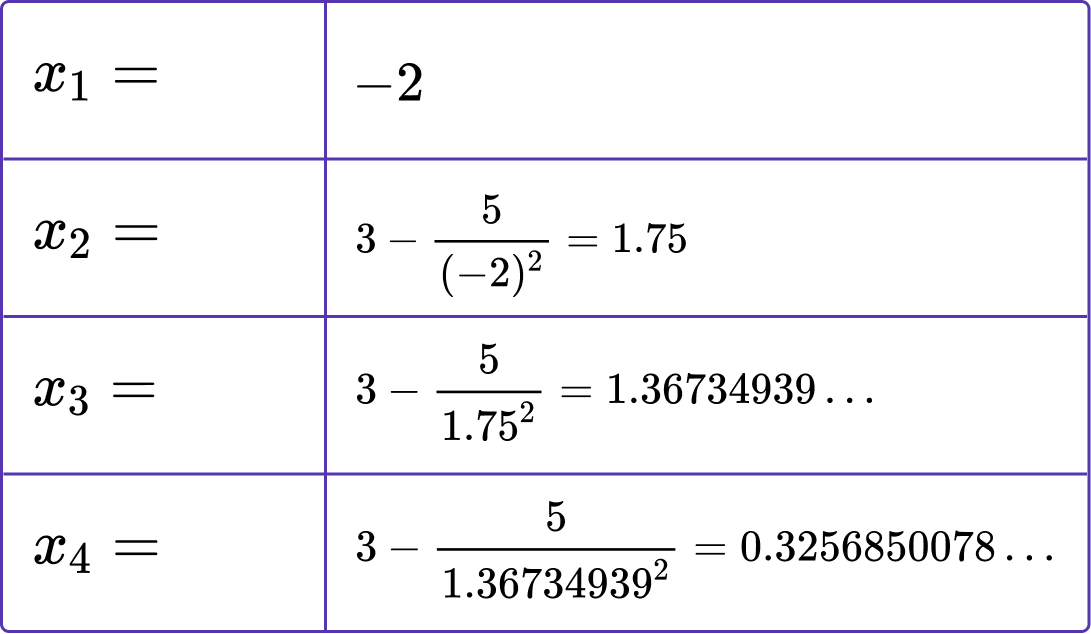
Iteration Maths practice question 6

x_{n+1}=\frac{\sqrt{x_{n}}-4}{10}

x_{n+1}=\frac{\sqrt{x_{n}}-10}{4}

x_{n+1}=16+10x_{n}^{2}

x_{n+1}=\frac{\sqrt{x_{n}+4}}{10}

\begin{aligned} \sqrt{x}-10x&=4\\\\ \sqrt{x}&=4+10x\\\\ \sqrt{x}-4&=10x\\\\ \frac{\sqrt{x}-4}{10}&=x\\\\ x_{n+1}&=\frac{\sqrt{x_{n}}-4}{10} \end{aligned}

Iteration maths GCSE questions

1. (a) Starting with $x_{0}=1$ and $x_{1}=1,$ use the iteration formula $x_{n+1}=x_{n-1}+x_n$ to determine the values of $x_{2}, \ x_{3},$ and $x_{4}.$

(b) Name the type of sequence generated by the iterative formula in part (a).

(4 marks)

Show answer

(a)

x_{2}=1+1=2

(1)

x_{3}=1+2=3

(1)

x_{4}=2+3=5

(1)

(b)

Fibonacci Sequence

(1)

2. (a) Show that $x^{2}+5x-6=0$ can be rearranged to give $x=\frac{6-x^2}{5}.$

(b) Starting with $x_{0}=0$ use the iterative formula to find $x_{3}.$

(7 marks)

Show answer

(a)

x_{2}+5x=6

(1)

5x=6-x^2

(1)

$x=\frac{6-x^2}{5}$ with division by $5$ shown.

(1)

(b)

x_{1}=\frac{6-0^2}{5}=1.2

(1)

x_{2}=\frac{6-1.2^2}{5}=0.912

(1)

x_{3}=\frac{6-0.912^2}{5}=1.0336512

(1)

(c)

$x_n$ is an approximate solution of the equation $x^{2}+5x-6=0.$

(1)

3. (a) Rearrange $x^{2}+1=3x$ to get $x=\sqrt{3x-1}.$

(b) Given that $x_{0}=3,$ use iteration to find the root of the equation $x^{2}+1=3x$ correct to $1$ decimal place.

(6 marks)

Show answer

(a)

x^{2}=3x-1

(1)

$x=\sqrt{3x-1}$ with the square root of both sides shown.

(1)

(b)

x_{n+1}=\sqrt{3x_{n}-1}

(1)

x_{1}=\sqrt{(3 \times 3)-1}=2.828427125

(1)

\begin{aligned} &x_{2}=\sqrt{(3 \times 2.828427125)-1}=2.735924227 \\ &x_{3}=\sqrt{(3 \times 2.735924227)-1}=2.684729536 \\ &x_{4}=\sqrt{(3 \times 2.684729536)-1}=2.655972253 \\ &x_{5}=\sqrt{(3 \times 2.655972253)-1}=2.639681185 \\ \end{aligned}

$x_{6}=\sqrt{(3 \times 2.639681185)-1}=2.630407488$ and minimum of $2$ values of $x_{n}$ above.

(1)

2.6 \ (1dp).

(1)

Learning checklist

You have now learned how to:

Find approximate solutions to equations numerically using iteration

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.