BIDMAS

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

Arithmetic Decimals Square numbers and square roots Cube numbers and cube roots Negative numbers Equivalent fractions

This topic is relevant for:

GCSE Maths Number Arithmetic

BIDMAS

Here we will learn about BIDMAS, including what it means and how to calculate and solve problems using BIDMAS.

There are also BIDMAS worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is BIDMAS?

BIDMAS is an acronym for the order or priority in which we complete mathematical operations (sometimes known as BODMAS or BEDMAS). Arithmetic operations such as multiplication and addition have to be completed in a specific order because of the nature of the function. This sequence of steps helps us to evaluate any mathematical calculation, both with numerical values and algebraic expressions.

To calculate using BIDMAS, you need to understand what BIDMAS represents and be able to apply the rules to any calculation.

BIDMAS stands for:

Brackets have a higher priority than indices and so we calculate what is inside a pair of brackets first. Indices have a higher priority than division and multiplication, so any index that can be evaluated is calculated next, and so on.

What is BIDMAS?

Order of operations

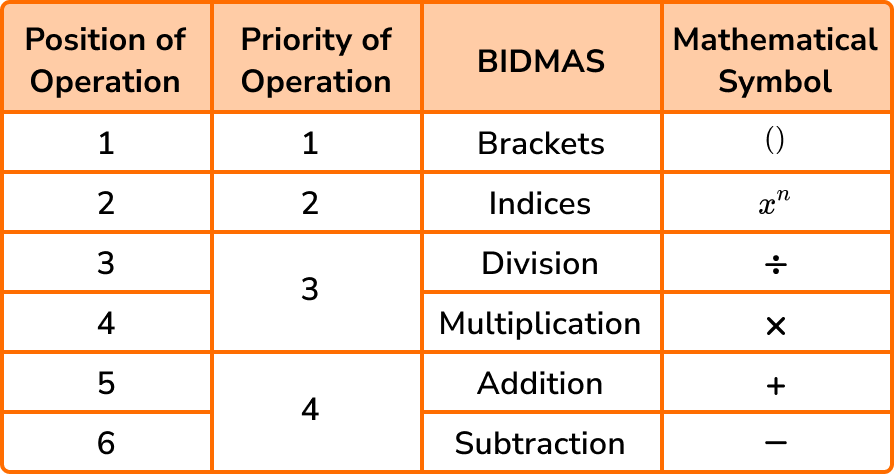
It is important to note that division and multiplication are given equal priority, and addition and subtraction are given equal priority.

When completing calculations that involve multiplication and division or addition and subtraction, we work from left to right.

For example,

Consider the sum $12-7+6$ ,

$12-7=5$ and then $5+6=11$ .

For example,

Consider the calculation $\frac{10}{5} \times 2$ ,

$10 \div 5=2$ and then calculate $2 \times 2 = 4$ .

Step-by-step guide: Fractions of an amount

Step-by-step guide: Collecting like terms

Visually we could represent BIDMAS as,

How to calculate using BIDMAS

In order to calculate using BIDMAS:

Resolve any calculations within brackets.
Resolve any indices (powers).
Resolve any divisions and multiplications.
Resolve any additions and subtractions.

Explain how to calculate using BIDMAS

BIDMAS worksheet

Get your free BIDMAS worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

BIDMAS worksheet

Get your free BIDMAS worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on arithmetic

BIDMAS is part of our series of lessons to support revision on arithmetic. You may find it helpful to start with the main arithmetic lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

BIDMAS examples

Example 1: BIDMAS with addition and multiplication

Calculate $3+6\times{7}.$

Resolve any calculations within brackets.

There are no brackets to resolve in this calculation.

2Resolve any indices (powers).

There are no indices to resolve in this calculation.

3Resolve any divisions and multiplications.

The multiplication that we need to calculate is $6\times{7}=42.$

Replacing $6\times{7}$ with $42$ gives us the calculation $3+42.$

4Resolve any additions and subtractions.

3+42=45

So $3+6\times{7}=45$ .

Example 2: BIDMAS with division and subtraction

Calculate $12-8\div{2}.$

Resolve any calculations within brackets.

There are no brackets to resolve in this calculation.

Resolve any indices (powers).

There are no indices to resolve in this calculation.

Resolve any divisions and multiplications.

The division we need to calculate is $8\div{2}=4$ .

Replacing $8\div{2}$ with $4$ gives us the calculation $12-4.$

Resolve any additions and subtractions.

12-4=8

So $12-8\div{4}=8$ .

Example 3: BIDMAS with brackets and multiplication

Calculate $3(2+4\times{6}-3).$

Resolve any calculations within brackets.

We have a pair of brackets and so we need to resolve what is inside the brackets first. This is the calculation, $2+4\times{6}-3$ .

Using BIDMAS, multiplication comes before addition and subtraction so we need to resolve the multiplication $4\times{6}=24$ .

Replacing $4\times{6}$ with $24$ in the calculation, we have $2+24-3.$

Addition and subtraction should be completed from left to right and so we have $2+24=26$ and $26-3=23.$ Therefore $2+24-3=23.$

As $2+4\times{6}-3=23$ and $3(2+4\times{6}-3)$ means $3\times(2+4\times{6}-3),$ we have the updated calculation $3\times{23}$ .

Resolve any indices (powers).

There are no indices to resolve in this calculation.

Resolve any divisions and multiplications.

3\times{23}=69

Resolve any additions and subtractions.

As there are no further calculations, we can state the solution.

$3(2+4\times{6}-3)=69$

Example 4: BIDMAS with an index and multiplication

Calculate $4\times{3}^{2}.$

Resolve any calculations within brackets.

There are no brackets to resolve in this calculation.

Resolve any indices (powers).

Here we have to resolve $3^{2}=3\times{3}=9$ .

Replacing $3^{2}$ with $9$ in the calculation, we now have

$4\times{9}$ .

Resolve any divisions and multiplications.

The final step needed is to calculate $4\times{9}=36$ .

Resolve any additions and subtractions.

There are no more calculations to resolve so the final solution is

$4\times{3}^{2}=36$ .

Example 5: BIDMAS with brackets, an index and a tricky division

Calculate $3+(10\div{4}\times{20})^{2}.$

Resolve any calculations within brackets.

Within the bracket we have the calculation $10\div{4}\times{20}$ .

We need to work from left to right.

Completing the division, we have $10\div{4}=2.5$ .

Next, $2.5\times{20}=50$ .

Therefore, $10\div{4}\times{20}=50$ .

Replacing $10\div{4}\times{20}$ with $50,$ we now have the updated calculation,

$3+50^{2}$ .

Resolve any indices (powers).

We now have to resolve $50^{2}=50\times{50}=2500$ .

Updating the calculation, we now have $3+2500$ .

Resolve any divisions and multiplications.

There are no divisions or multiplications to resolve.

Resolve any additions and subtractions.

$3+2500=2503$ which gives us the final solution,

$3+(10\div{4}\times{20})^{2}=2503$ .

Example 6: BIDMAS with everything

Calculate $4^{2}+2(14-8)\div{3}.$

Resolve any calculations within brackets.

Within the brackets is the calculation $14-8=6$ .

Updating the calculation by changing the value in the bracket to 6, we have

$4^{2}+2\times{6}\div{3}$ .

Resolve any indices (powers).

As $4^{2}=4\times{4}=16,$ we now have

$16+2\times{6}\div{3}$ .

Resolve any divisions and multiplications.

Here we have to calculate $2\times{6}\div{3}.$ Working from left to right, we calculate $2\times{6}$ and then divide the solution by $3.$

$2\times{6}=12$

$12\div{3}=4$

Updating the calculation, we now have $16+4.$

Resolve any additions and subtractions.

As $16+4=20,$ our final solution is

$4^{2}+2(14-8)\div{3}=20$ .

Example 7: BIDMAS with fractions

Calculate $\frac{(3+2)^{2}\times{8}}{16-2^{3}}.$

Resolve any calculations within brackets.

When presented with a fraction, treat the numerator and the denominator separately, and then resolve the fraction.

The numerator has a pair of brackets containing the sum $3+2=5$ .

The denominator does not contain a pair of brackets.

Updating the calculation, we now have $\frac{5^{2}\times{8}}{16-2^{3}}.$

Resolve any indices (powers).

The numerator contains the index $5^{2}=5\times{5}=25$ .

The denominator has the index $2^{3}=2\times{2}\times{2}=8$ .

Updating the calculation, we now have $\frac{25\times{8}}{16-8}.$

Resolve any divisions and multiplications.

The numerator has the multiplication $25\times{8}=200$ .

The denominator does not contain any multiplications or divisions.

Updating the calculation, we now have $\frac{200}{16-8}.$

Resolve any additions and subtractions.

The numerator does not contain any further calculations.

The denominator contains the subtraction $16-8=8$ .

Updating the fraction, we now have $\frac{200}{8}$ which is the same as $200\div{8}=25$ .

Our final answer is $\frac{(3+2)^{2}\times{8}}{16-2^{3}}=25.$

Common misconceptions

Multiplication and division/addition and subtraction in the incorrect order

When we have a chain of multiplications and divisions or a chain of additions and subtractions, we work from left to right.

For example, if we put brackets into the calculation $12\div{4}\times{3}$ with the purpose of keeping the calculation exactly the same, we must place the brackets around $12\div{4}.$ This is because $12\div{4}\times{3}=9,$ and $(12\div{4})\times{3}=3\times{3}=9.$

If we placed brackets around $4\times{3}$ we would have $12\div{(4\times{3})}=12\div{12}=1$ which is not the same solution that we would get without the brackets.

BIDMAS with fractions

The temptation is to carry out the division on everything too soon as a fraction is a division. However, treat the numerator and the denominator as if they have a hidden pair of brackets around them, you must resolve each bracket first, and then carry out the division last. For example,

$\frac{2+3}{4+6}=\frac{(2+3)}{(4+6)}=\frac{5}{10}=0.5.$

Multiplying before Indices

Take $2\times{3}^{4}.$ As we perform indices before we perform multiplication within BIDMAS, we need to calculate the index term first, and then multiply the solution by $2.$ Inserting a pair of brackets with the purpose of keeping the calculation exactly the same, $2\times{3}^{4}=2\times(3^{4})=162.$

A common misconception is that the multiplication is carried out first, and then the value is raised to the power; here this would look like $(2\times{3})^{4}$ and is equal to $6^{4}=1296$ which is the wrong answer.

Practice BIDMAS questions

88

46

640

118

\begin{aligned} 6+5\times{8}& =\ 6+40\\\\ &=\ 46 \end{aligned}

0.\dot{3}

1.3

9

11

\begin{aligned} 16-15\div{3} &= 16-5\\\\ &=\ 11 \end{aligned}

17

1

-1

11

\begin{aligned} (8-2\times{5}+4)\div{2} &=\ (8-10+4)\div{2}\\\\ &=\ (-2+4)\div{2}\\\\ &=\ 2\div{2}\\\\ &=\ 1 \end{aligned}

20

100

50

49

\begin{aligned} 2\times{5}^{2}&=\ 2\times{25}\\\\ &=\ 50 \end{aligned}

33

255.\dot{2}

228

-33

\begin{aligned} 258-(10\div{2}\times{3})^{2} &=\ 258-(5\times{3})^{2}\\\\ &=\ 258-15^{2}\\\\ &=\ 258-225\\\\ &=\ 33 \end{aligned}

2.4

7

8

12

\begin{aligned} 3(7-5)^{3}\div{6}+4&=\ 3\times{2}^{3}\div{6}+4\\\\ &=\ 3\times{8}\div{6}+4\\\\ &=\ 24\div{6}+4\\\\ &=\ 4+4\\\\ &=\ 8 \end{aligned}

2

4

8

12

\begin{aligned} \frac{(16-4)^{2}\div{3}^{2}}{\sqrt{4}}&=\frac{12^{2}\div{3}^{2}}{\sqrt{4}}\\ \\ &= \frac{144\div{9}}{2}\\ \\ &= \frac{16}{2}\\\\ &= 8 \end{aligned}

BIDMAS GCSE questions

1. (a) Work out $\frac{-4\times{-3}}{-6}.$

(b) Add brackets to make the statement correct:

2+3\times{6}-4=8

(5 marks)

Show answer

(a)

-4\times{-3}=12

(1)

12\div{-6}=-2

(1)

(b)

2+3\times(6-4)=8

(1)

(c)

\sqrt{9}=3

(1)

3\times{3}=9

(1)

2. (a) Put two operations into each calculation so that the answer is correct.

BIDMAS gcse question 2 image 1

(b) Add brackets to make the statement correct:

2+3\times{4}-5=-5

(6 marks)

Show answer

(a)

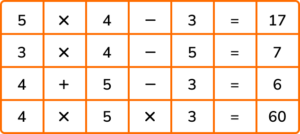
BIDMAS gcse question 2 image 3

(4)

(b)

$(2+3)$ or $(4-5)$

(1)

(2+3) \times (4-5)

(1)

3. (a) Murphy and Nick calculate different answers to the question:

Calculate $6+7\times 8.$

Murphy says: $6+7\times 8=104.$

Nick says: $6+7\times 8=62.$

Who is correct? Explain your answer.

(b) Add a pair of brackets to the incorrect answer to part (a) to correct the statement.

(3 marks)

Show answer

(a)

Nick is correct.

(1)

6+7\times{8}=6+56=62

(1)

(b)

(6+7)\times{8}=104

(1)

Learning checklist

You have now learned how to:

Use knowledge of the order of operations to carry out calculations involving the

4

operations

Explore the order of operations using brackets

Use conventional notation for the priority of operations, including brackets, powers, and roots

The next lessons are

Did you know?

The acronym PEMDAS is the American version of the same rules.

Here, a set of parentheses are brackets, and exponents are indices. The acronym would therefore read: Parenthesis, Exponents, Multiplication and Division, Addition and Subtraction. The order can be remembered using the phrase ‘Please Excuse My Dear Aunt Sally’.

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.