Volume of a sphere

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

Multiplying fractions Substitution Area of a circle Rounding

This topic is relevant for:

GCSE Maths Geometry and Measure 3D Shapes Sphere

Volume Of A Sphere

Here we will learn about the volume of a sphere, including how to calculate the volume of a sphere given its radius and how to find the volume of a hemi-sphere.

There are also volume of a sphere worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the volume of a sphere?

The volume of a sphere is the amount of space inside a sphere.

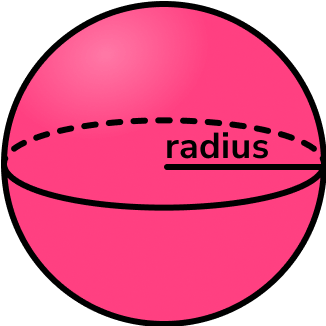
To calculate the volume of a sphere, we use the formula,

$V=\frac{4}{3} \pi r^3$ .

Notice the cube of the radius $(r^3)$ is in the volume formula. Volume is a measure in three-dimensions so the units for the volume are units cubed.

For example, find the volume of the sphere with a radius of $5 \; cm$ .

\begin{aligned} \text{Volume}&=\frac{4}{3} \pi r^3 \\\\ &= \frac{4}{3} \times \pi \times 5^3\\\\ &=\frac{500}{3}\pi\\\\ &=524.6 \ cm^3 \ \text{to 1 dp} \end{aligned}

What is the volume of a sphere?

How to calculate the volume of a sphere

In order to calculate the volume of a sphere:

Write down the formula for the volume of a sphere.
Substitute given values into the formula.
Complete the calculation.
Write the answer, including the units.

Explain how to calculate the volume of a sphere

Volume and surface area of a sphere worksheet

Get your free volume and surface area of a sphere worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Volume and surface area of a sphere worksheet

Get your free volume and surface area of a sphere worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on sphere

Volume of a sphere is part of our series of lessons to support revision on sphere. You may find it helpful to start with the main sphere lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Volume of a sphere examples

Example 1: volume of a sphere given the radius

Calculate the volume of a sphere with radius $6 \; cm$ . Write your answer to $1$ decimal place.

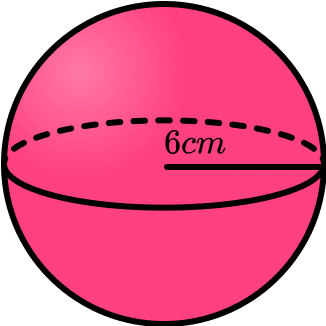
Write down the formula for the volume of a sphere.

The formula for the volume of a sphere is $V=\frac{4}{3} \pi r^3$ .

2Substitute the given values into the formula.

We need to substitute the value of the radius $r=6$ into the formula.

V=\frac{4}{3} \times \pi \times 6^3

3Complete the calculation.

Use a calculator to work out the volume.

V=288 \pi =904.7786842...

4Write the answer, including the units.

Here we are asked to give the answer to $1$ decimal place.

The volume of the sphere is $904.8 \; cm^3 \; (1dp)$ .

Example 2: decimal radius

Find the volume of a sphere with radius $7.2 \; cm$ . Write your answer to $2$ decimal places.

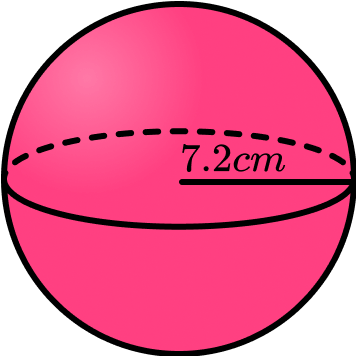
Write down the formula for the volume of a sphere.

V=\frac{4}{3} \pi r^3

Substitute the given values into the formula.

Substituting the value $r=7.2 \; cm$ into the formula for the volume of a sphere, we have

$V=\frac{4}{3} \times \pi \times 7.2^3$ .

Complete the calculation.

Use a calculator to work out the volume.

$V=1563.457566...$

Write the answer, including the units.

Here we are asked to write the answer to $2$ decimal places.

$V= 1563.457566… = 1563.46 \; cm^3 \; (2dp)$

The volume of the sphere is $1563.46 \; cm^3 \; (2dp)$ .

Example 3: volume of a sphere given the diameter – in terms of pi

Calculate the volume of a sphere with a diameter of $6m.$ Write your answer in terms of $\pi$ .

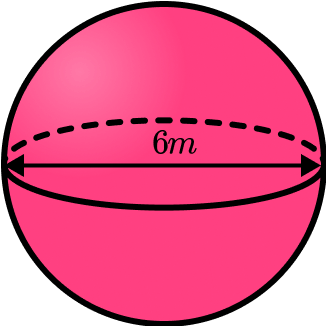
Write down the formula for the volume of a sphere.

V=\frac{4}{3} \pi r^3

Substitute the given values into the formula.

The radius is half the length of the diameter and so

$r=6\div{2}=3\text{m}.$

We need to substitute the value of the radius into the formula.

$V=\frac{4}{3} \times \pi \times 3^3$

Complete the calculation.

V=36\pi

Write the answer, including the units.

Here we are asked to write the answer in terms of $\pi$ .

$V= 36\pi \text{ m}^3$

The volume of the sphere is $36\pi \text{ m}^3$ .

Example 4: volume of a hemisphere

Find the volume of a hemisphere with radius $8 \; cm$ . Write your answer to $1$ decimal places.

Write down the formula for the volume of a sphere.

A hemisphere has half the volume of a sphere, so we need to divide the volume of a sphere by $2$ ,

$V=\frac{4}{3} \pi r^3 \div{2}$ .

Substitute the given values into the formula.

Given that $r=8$ , we have

$V=\frac{4}{3} \times \pi \times 8^3\div{2}$ .

Complete the calculation.

Use a calculator to work out the volume.

$V=\frac{1024}{3}\pi$

Write the answer, including the units.

Here we are asked to write the answer to $1$ decimal places.

$V=\frac{1024}{3}\pi = 1072.330292… = 1072.3 \text{ cm}^3 \ \text{(1dp)}$

The volume of the hemisphere is $1072.3 \; cm^3$ .

Example 5: volume of a hemisphere

Find the volume of a hemisphere with radius $12.5 \; cm$ . Give your answer to $2$ decimal places

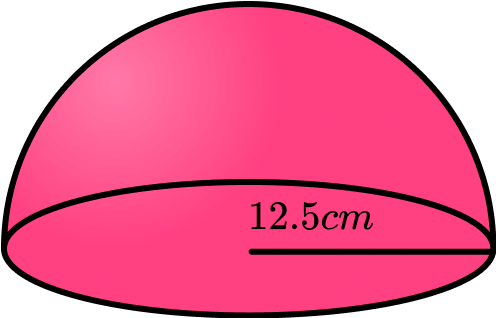
Write down the formula for the volume of a sphere.

Remember we have a hemisphere so we need to halve the volume of the equivalent sphere.

$V=\frac{4}{3} \pi r^3 \div{2}$

Substitute the given values into the formula.

We need to substitute the value of the radius into the formula.

$V=\frac{4}{3} \times \pi \times 12.5^3\div{2}$

Complete the calculation.

Use a calculator to work out the volume.

$V=4090.615434...$

Write the answer, including the units.

Here we are asked to give the answer to $2$ decimal places.

$V=4090.615434...=4090.62 \; cm^3 \; (2dp)$

The volume of the hemisphere is $4090.62 \; cm^3 \; (2dp)$ .

Calculating the radius given the volume

In order to calculate the radius of a sphere given the volume, we need to rearrange the formula for the volume of a sphere $(V=\frac{4}{3}\pi r^3)$ to make $r$ (the radius) the subject of the formula.

Now we have the formula for determining the radius of a sphere given the volume to be,

$r=\sqrt[3]{\frac{3V}{4\pi}}$ .

How to calculate the radius of a sphere given the volume

In order to calculate the radius of the sphere given the volume:

Write down the formula for the radius of a sphere, in terms of the volume.
Substitute the given values into the formula.
Complete the calculation.
Write the answer, including the units.

Calculating the radius of a sphere examples

Example 6: calculating the radius given the volume

The volume of a sphere is $3000 \; cm^3$ . Calculate the radius of the sphere, correct to $2$ decimal places.

Write down the formula for the radius of a sphere, in terms of the volume.

r=\sqrt[3]{\frac{3V}{4\pi}}

Substitute the given values into the formula.

We are given the volume, so we can substitute this into the formula to calculate the radius,

$r=\sqrt[3]{\frac{3\times{3000}}{4\pi}}$ .

Complete the calculation.

\begin{aligned} r&=\sqrt[3]{\frac{9000}{4\pi}} \\\\ &=\sqrt[3]{716.1972439...} \\\\ &=8.947002289... \end{aligned}

Write the answer, including the units.

Here we are asked to give the answer to $2$ decimal places.

$r=8.947002289...=8.95 \; cm \; (2dp)$

The radius of the sphere is $8.95 \; cm \; (2dp)$ .

Example 7: calculating the radius given the volume

Calculate the radius of a sphere with the volume $8460 \; m^3$ . Write your answer to the nearest centimetre.

Write down the formula for the radius of a sphere, in terms of the volume.

Here we need to use

$r=\sqrt[3]{\frac{3V}{4\pi}}$ .

Substitute the given values into the formula.

Substituting the value for the volume, we have

$r=\sqrt[3]{\frac{3\times{8460}}{4\pi}}$ .

Complete the calculation.

\begin{aligned} r&=\sqrt[3]{\frac{25380}{4\pi}} \\\\ &=\sqrt[3]{2019.676228...} \\\\ &=12.64039323... \end{aligned}

Write the answer, including the units.

Here we are asked to give the answer to the nearest centimetre.

$r=12.64039323...=12.64 \; m=1264 \; cm$

The radius of the sphere is $1264 \; cm$ .

Common misconceptions

Using the correct formula

There are several formulas that can be used, so we need to match the correct formula to the correct context.

Rounding

It is important to not round the answer until the end of the calculation. This will mean your final answer is accurate. It is useful to keep your answer in terms of $\pi$ until you round the answer at the very end of the question.

Make sure you have the correct units

For area we use square units such as $cm^2$ .

For volume we use cube units such as $cm^3$ .

Using the radius or the diameter

It is a common error to mix up radius and diameter. Remember the radius is half of the diameter.

Practice volume of a sphere questions

4188.8 \; cm^3

314.2 \; cm^3

1.3 \; cm^3

1256.6 \; cm^3

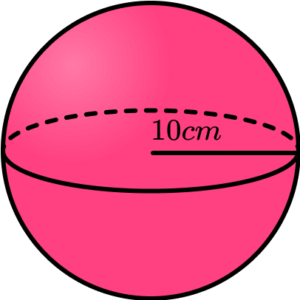
We are finding the volume of a sphere so we substitute the value of $r$ into the formula.

\begin{aligned} V&=\frac{4}{3} \pi r^3 \\\\ &= \frac{4}{3} \times \pi \times 10^3\\\\ &=\frac{4000}{3}\pi\\\\ &=4188.790205… \\\\ &=4188.8 \ cm^3 \ \text{(1dp)} \end{aligned}

10536.7 \; cm^3

2324.3 \; cm^3

1317.1 \; cm^3

581.1 \; cm^3

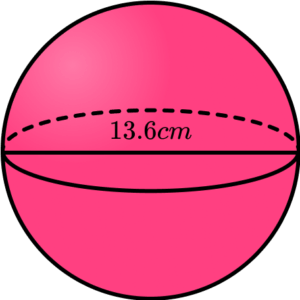
The radius is half the value of the diameter and so $r=13.6 \div 2=6.8 \; cm.$
Substituting $r=6.8$ into $V=\frac{4}{3} \pi r^3$ , we have
$\begin{aligned} V&=\frac{4}{3} \pi r^3 \\\\ &= \frac{4}{3} \times \pi \times 6.8^3\\\\ &=1317.089682… \\\\ &=1317.1\text{cm}^3\text{ (1dp)} \end{aligned}$

243\pi \; m^3

108\pi \; m^3

972\pi \; m^3

729\pi \; m^3

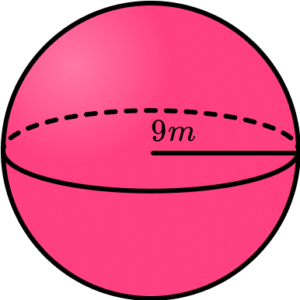
Substituting $r=9$ into the formula for the volume of a sphere, we have

\begin{aligned} V&=\frac{4}{3} \pi r^3 \\\\ &= \frac{4}{3} \times \pi \times 9^3\\\\ &=972\pi \end{aligned}

33510 \; mm^3

16755 \; mm^3

1257 \; mm^3

3770 \; mm^3

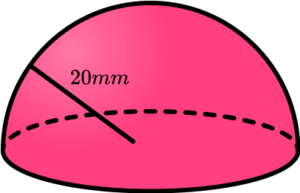
We are finding the volume of a hemisphere, so we need half of the volume of a sphere.

\begin{aligned} V&= (\frac{4}{3} \pi r^3) \div{2}\\\\ &= (\frac{4}{3} \times \pi \times 20^3) \div{2}\\\\ &=\frac{16 000}{3} \pi\\\\ &=16 755.16082… \\\\ &=16 755 \text{ mm}^3\text{ (0dp)} \end{aligned}

2304\pi \; km^3

7240 \; km^3

1152\pi \; km^3

3620 \; km^3

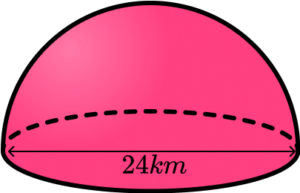
We are finding the volume of a hemisphere, so we need to calculate half of the volume of a sphere.

\begin{aligned} V&=\frac{4}{3} \pi r^3 \div{2}\\\\ &= \frac{4}{3} \times \pi \times 12^3 \div{2}\\\\ &=1152\pi \\\\ &=1152\pi \ km^3 \end{aligned}

7.1 \; cm

18.9 \; cm

37.8 \; cm

11.3 \; cm

Using the formula for the radius in terms of the volume, we substitute the value of the volume and solve to find the radius.

\begin{aligned} r&=\sqrt[3]{\frac{3V}{4\pi}} \\\\ &=\sqrt[3]{\frac{3\times15000}{4\pi}} \\\\ &=\sqrt[3]{358.098622…} \\\\ &=7.101240423… \\\\ &=7.1 \; cm \; (1dp) \end{aligned}

Volume of a sphere GCSE questions

\text{Volume of a sphere}=\frac{4}{3} \pi r^3

1. Here is a sphere with a radius $10.4 \; cm.$

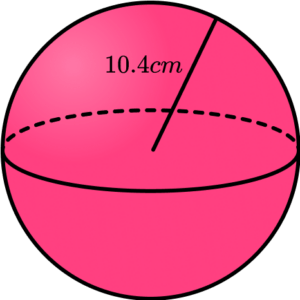
Calculate the volume of the sphere. Write your answer to $1$ decimal place.

(2 marks)

Show answer

V=\frac{4}{3} \times \pi \times 10.4^3

(1)

4711.8 \; cm^3

(1)

2. (a) A model globe has a diameter of $30 \; cm.$ Calculate the volume of the globe in terms of $\pi$ .

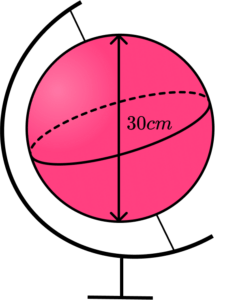
(b) The mass of the model globe is $1.2kg,$ excluding the frame. Calculate the density in $g/cm^3$ of the model, to $2$ decimal places.

(4 marks)

Show answer

(a)

V=\frac{4}{3} \times \pi \times 15^3

(1)

4500\pi

(1)

(a)

\text{Density }=1200\div{4500\pi}

(1)

D=0.08\text{ g/cm}^3

(1)

3. A ceramic bowl is in the shape of a hemisphere. The bowl has a radius $25 \; cm.$

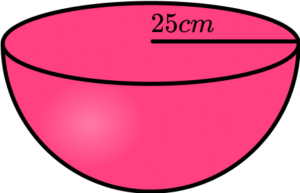
Water fills the bowl at a rate of $500 \; cm^3$ per minute. How long does it take to fill the bowl? Write your answer to the nearest second.

(3 marks)

Show answer

\frac{4}{3} \times \pi \times 25^3 \div{2}= \frac{31 250}{3} \pi = 32724.92347…

(1)

$32 724.923… \div 2000=16.36246174…$ or $\frac{125}{24}\pi$

(1)

$16.36246174\dots$ minutes $= 16$ minutes $22$ seconds

(1)

Learning checklist

You have now learned how to:

Calculate the volume of a sphere

Calculate the volume of a hemisphere

Solve problems involving the volume of a sphere

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.