Cuboid

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

2D shapes Types of quadrilaterals Area of a rectangle Substituting into formulae

This topic is relevant for:

GCSE Maths Geometry and Measure 3D Shapes

Cuboid

Here we will learn about cuboids, including nets of cuboids and volume and surface area of cuboids.

There are also volume and surface area of a cuboid worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a cuboid?

A cuboid (or a rectangular cuboid) is a polyhedron ( $3$ D shape) with $6$ rectangular faces. They can also be called rectangular prisms.

Cubes are a special type of cuboid where the length, width and height are all equal.

Examples of cuboids:

Cuboid Image 1

Cuboid Image 2

What is a cuboid?

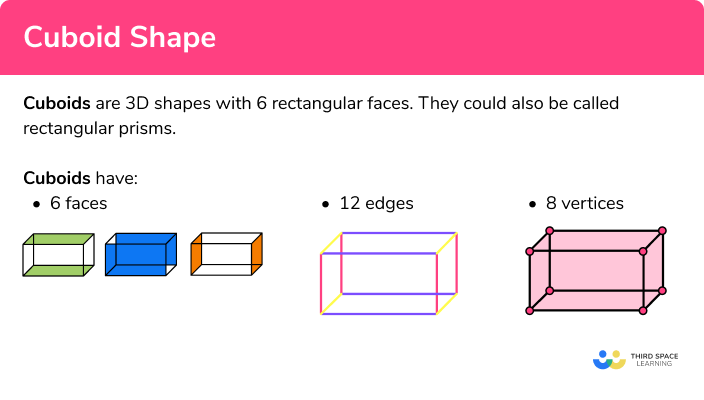
Faces

A face of a $3$ D shape is a flat surface.

Cuboids have a total of $\bf{6}$ faces – all of which are rectangular (or square) and contain four right angles. They have three pairs of identical faces:

Cuboid Image 3

Cuboid Image 4

Cuboid Image 5

Edges

An edge of a $3$ D shape is a straight line between two faces.

Cuboids have $\bf{12}$ edges:

Vertices

A vertex is a point where two or more edges meet.

Cuboids have $\bf{8}$ vertices:

Nets

A net of a three-dimensional shape is the $2$ dimensional shape it would make if it were unfolded and laid flat. Nets can be folded up to make the $3$ D shapes.

Labelling a cuboid

We can label the vertices (corners) of a cuboid to help us identify certain edges or faces.

E.g.

Using this labelling we can identify lengths, e.g. the length $AB$ :

We can also identify faces, e.g. the face $ABCD$ :

Volume of a cuboid

The volume of a $3$ D shape is how much space there is inside of the shape.

The formula for the volume of a cuboid is:

Volume = length \times width \times height

E.g.

This cuboid is made from $12$ cubes.

Its volume is

\begin{aligned} &Volume = length \times width \times height \\\\ &Volume = 2 \times 2 \times 3 \\\\ &Volume = 12cm^3 \end{aligned}

Volume is measured in cubic units, e.g. $mm^3, \ cm^3$ or $m^3.$

Step-by-step guide: Volume of a cuboid

See also: Volume of a cube

Cuboid worksheet

Get your free cuboid worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Cuboid worksheet

Get your free cuboid worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Volume of a cuboid example

Work out the volume of this cuboid

Substitute the values into the formula.

Here the length is $7cm$ , the width is $12cm$ and the height is $2cm$ .

\begin{aligned} &Volume = length \times width \times height \\\\ &Volume = 7 \times 12 \times 2 \end{aligned}

2Do the calculation.

\begin{aligned} &Volume = 7 \times 12 \times 2 \\\\ &Volume = 168\end{aligned}

3Include the units.

The measurements are in cm therefore the volume will be in $cm^3$ .

Volume=168cm^3

Surface area of a cuboid

The surface area of a $3$ D shape is the total area of all of the faces of the shape

To work out the surface area of a cuboid, we need to work out the area of each rectangular face and add them all together.

Cuboids have three pairs of equal faces – top and bottom, front and back, and left and right.

Since it is an area, surface area is measured in square units (e.g. $mm^2, cm^2, m^2$ etc).

Face	Area
Bottom	5 × 6 = 30
Top	30
Front	6 × 2 = 12
Back	12
Right side	2 × 5 = 10
Left side	10

\begin{aligned} \text{Total Surface Area } &= 30 + 30 + 12 + 12 + 10 + 10 \\\\ &= 104cm^2 \end{aligned}

Step-by-step guide: Surface area of a cuboid

See also: Surface area of a cube

Surface area of a cuboid example

Work out the surface area of the cuboid

Work out the area of each face.

We know that the areas of the top and bottom are equal, the front and back are equal and the two sides are equal.

Face	Area
Bottom	7 × 12 = 84
Top	84
Front	7 × 2 = 14
Back	14
Right side	2 × 12 = 24
Left side	24

2Add the six areas together.

84+84+14+14+24+24=244

3Include the units.

The measurements on the cuboid are in cm therefore the total surface area of the cuboid $= 244cm^2.$

Common misconceptions

Missing/incorrect units

You should always include units in your answer.
Volume is measured in units cubed (e.g. $mm^3, cm^3, m^3$ etc)
Surface area is measured in units squared (e.g. $mm^2, cm^2, m^2$ etc)

Calculating with different units

You need to make sure all measurements are in the same units before calculating volume or surface area. (E.g. you can’t have some in $cm$ and some in $m$ )

Dividing by three rather than cube rooting

If you are given the volume of a cube and you need to find the side length, remember the inverse of cubed is cube root, not divide by $3.$

E.g.

If the volume of a cube is $8cm^3$ , the side length is $\sqrt[3]{8}=2cm$ (not $8\div3$ )

Calculating volume instead of surface area

Volume and surface area are different things – volume tells us the space within the shape whereas surface area is the total area of the faces. To find surface area, work out the area of each face and add them together.

Equal faces

A common mistake is to think that four of the faces are equal.

E.g.

The pair of blue faces are equal to each other.

The pair of green faces are equal to each other.

The pair of oranges faces are equal to each other.

Cuboid vs parallelepiped

A common error is to confuse a rectangular cuboid with a rectangular parallelepiped. Cuboids have $6$ rectangular faces whereas parallelepipeds have $6$ faces that are parallelograms.

Practice cuboid questions

90\mathrm{mm}^{3}

332\mathrm{mm}^{3}

360\mathrm{mm}^{3}

160\mathrm{mm}^{3}

\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ \text{Volume }&= 4 \times 10 \times 9\\\\ \text{Volume }&=360\mathrm{mm}^{3} \end{aligned}

6\mathrm{cm}^{3}

600\mathrm{cm}^{3}

60\mathrm{cm}^{3}

598\mathrm{cm}^{3}

Notice that some of the units are in cm and some in $m$ so the first thing we need to do is convert $0.25m$ to $cm. \ 0.25m=25cm.$

\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ \text{Volume }&= 3 \times 25 \times 8\\\\ \text{Volume }&=600\mathrm{cm}^{3} \end{aligned}

2cm

150cm

50cm

12cm

\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ 300&= 25 \times 6 \times h\\\\ 300&=150h\\\\ h&=2\mathrm{cm} \end{aligned}

990\mathrm{m}^{2}

792\mathrm{m}^{2}

492\mathrm{m}^{2}

642\mathrm{m}^{2}

Work out the area of each of the six faces:

Face	Area
Bottom	6 × 15 = 90
Top	90
Front	6 × 11 = 66
Back	66
Right side	11 × 15 = 165
Left side	165

\text{Total surface area: }90+90+66+66+165+165=642\mathrm{m}^{2}

621\mathrm{cm}^{2}

9000\mathrm{cm}^{2}

2700\mathrm{cm}^{2}

3000\mathrm{cm}^{2}

First we need to make all the units the same. $0.3m=30cm.$

Then work out the area of each of the six faces:

Face	Area
Bottom	20 × 30 = 600
Top	600
Front	20 × 15 = 300
Back	300
Right side	30 × 15 = 450
Left side	450

\text{Total surface area: } 600+600+300+300+450+450=2700\mathrm{cm}^{2}

(140+38a) \ \mathrm{cm}^{2}

(140+56a) \ \mathrm{cm}^{2}

70a \ \mathrm{cm}^{2}

140a \ \mathrm{cm}^{2}

Work out the area of each of the six faces:

Face	Area
Bottom	14 × a = 14a
Top	14a
Front	14 × 5 = 70
Back	70
Right side	5 × a = 5a
Left side	5a

\text{Total surface area: }14a+14a+70+70+5a+5a=(140+38a) \ \mathrm{cm}^{2}

Cuboid GCSE questions

1. Calculate the surface area of the cuboid. Give your answer in $m^2.$

Cuboid GCSE Question 1

(3 marks)

Show answer

240cm=2.4m

(1)

\text{Surface area } = 2.8+2.8+9.6+9.6+1.68+1.68

(1)

\text{Surface area }=28.16\mathrm{m}^{2}

(1)

2. (a) Each of these diagrams is made from 6 identical squares with side length $7cm$ . Which diagram is the net of a cube?

Cuboid GCSE Question 2

(b) What would the volume of the cube made from this net be?

(3 marks)

Show answer

(a)

D – cao

(1)

(b)

\text{Volume }=7 \times 7 \times 7

(1)

\text{Volume }=343\mathrm{cm}^{3}

(1)

3. The volume of a cube is $125\mathrm{cm}^{3}$ .

What is the surface area of the cube?

(4 marks)

Show answer

\text{Side length of cube }=\sqrt[3]{125}

(1)

\text{Side length of cube }= 5cm

(1)

\text{Area of each face }=5 \times 5 = 25

(1)

\text{Total surface area }=6 \times 25 = 150\mathrm{cm}^{2}

(1)

Learning checklist

You have now learned how to:

Recognise a cuboid or a cube

Calculate the volume of a cuboid

Calculate the surface area of a cuboid

Apply formulae to calculate and solve problems involving cuboids (including cubes)

Use the properties of faces, surfaces, edges and vertices of cubes and cuboids to solve problems in 3-D

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.