GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
Angles in polygons Types of quadrilaterals Angles in parallel lines BearingsThis topic is relevant for:

Types Of Triangles
Here we will learn about types of triangles, including their names, their properties and applying them to problems.
There are also types of triangles worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is a triangle?
A triangle is a 2D shape with 3 straight sides and 3 vertices. You need to be able to classify triangles based on their properties, and find unknown angles and side lengths.
What is a triangle?
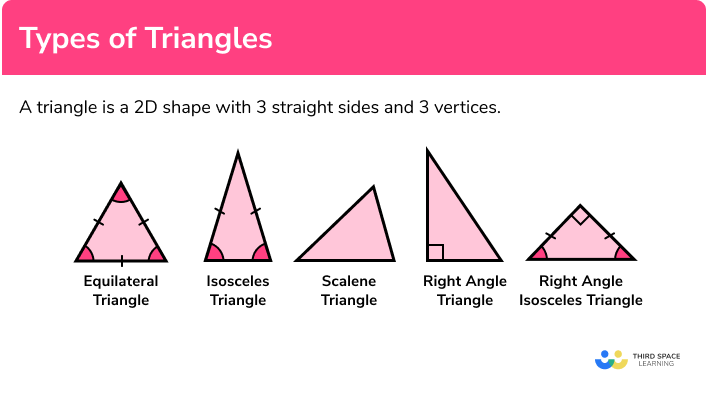
Types of triangles
There are 5 different types of triangle. Below is a table that describes the properties of each triangle.
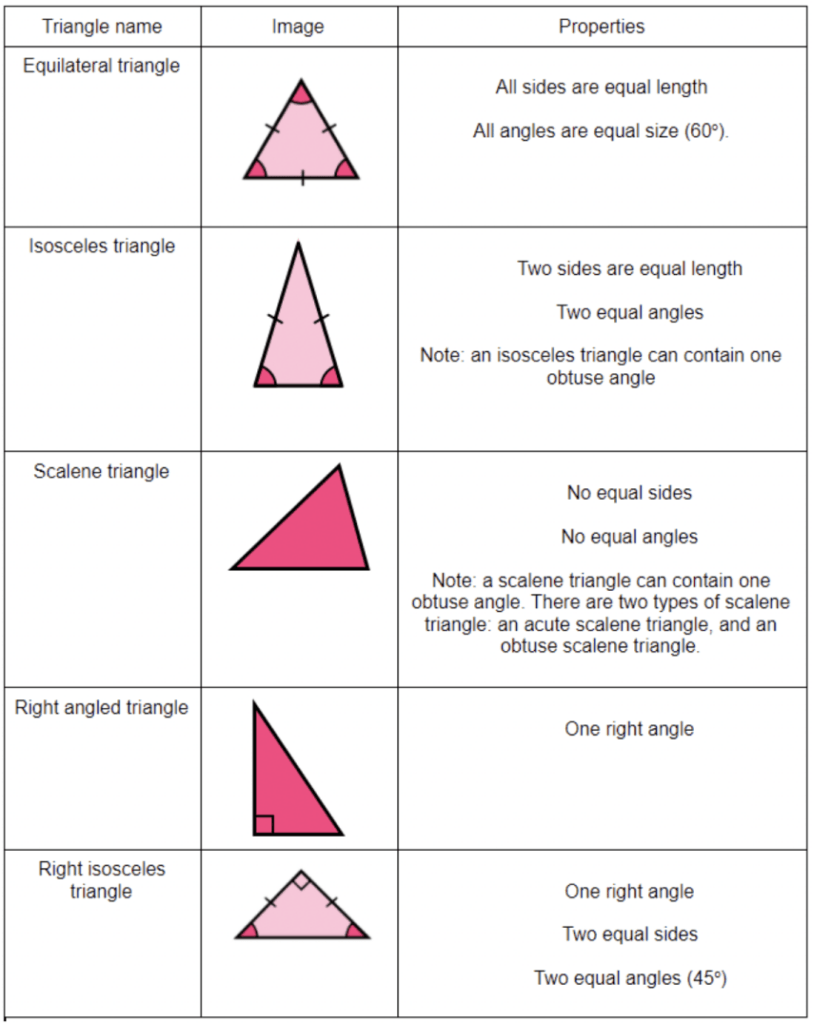
Properties of triangles are very important within geometry. They are one of the most common shapes to recognise for angles in parallel lines, circle theorems, interior angles, trigonometry, Pythagoras’ theorem, and many more. You therefore must be familiar with their individual properties.
Triangle properties
We need to know the types of triangles and their properties. We know that all triangles have 3 sides and 3 angles. We also need to recognise that there are lots of different types of triangles and they are all unique because of the collection of properties each shape may have.
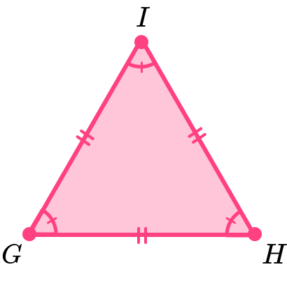
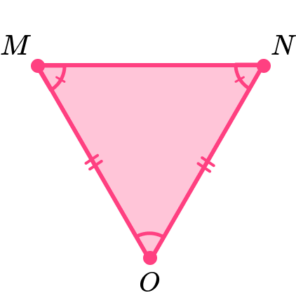
We can recognise equilateral triangles because they have 3 equal sides and 3 equal angles. Equal sides are often labelled with dashes.
E.g.
We can recognise isosceles triangles because they have 2 equal sides and 2 equal angles. The 2 equal angles are the base angles of the isosceles triangle.
E.g.
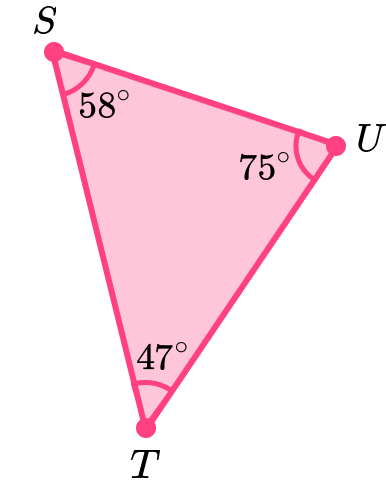
We can recognise scalene triangles because all the sides are different and all the angles are different.
E.g.
We can recognise right angled triangles because they have one right angle.
E.g.

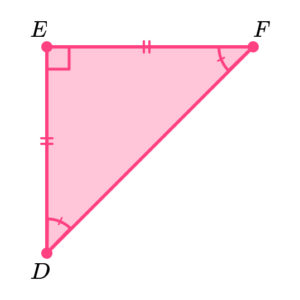
We can recognise right angled isosceles triangles because they have 1 right angle, 2 equal sides and 2 equal angles.
E.g.
We can use these properties to solve problems and find missing angles.
E.g.
Is this statement true or false?
An equilateral triangle has three equal sized side lengths and two equal sized angles.
Answer: False
Equilateral triangles have 3 equal sides and 3 equal angles.
E.g.
Find the missing angle.
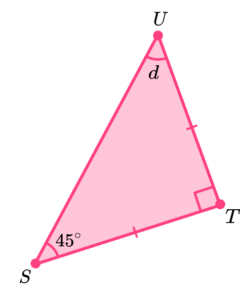
Answer:
This is a right angled isosceles triangle because it has 1 right angle and 2 equal sides marked with a dash.
So, Angle d=45°.
Angles in a triangle
Triangles can contain acute angles, a right angle, or one obtuse angle.
A triangle cannot contain more than one right angle, obtuse angle, or a reflex angle. The only two types of triangles that can contain an obtuse angle are an isosceles triangle and a scalene triangle.
E.g.
Here are two examples of these obtuse triangles:
The sum of angles in a triangle is 180° .
This property helps to find angles in any polygon as a polygon can be triangulated (split into triangles) and therefore the interior angles can be calculated.
Step-by-step guide: Angles in a triangle
How to classify a triangle
In order to classify a triangle:
- Determine the size of the angles/side lengths within the triangle.
- Recognise the other properties of the triangle.
How to classify a triangle

Types of triangles worksheet

Get your free types of triangles worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Types of triangles worksheet

Get your free types of triangles worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on triangles
Types of triangles is part of our series of lessons to support revision on polygons and triangles. You may find it helpful to start with the main triangles lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Types of triangles examples
Example 1: triangle
Correctly classify the following polygon:
- Determine the size of the angles/side lengths within the triangle.
Angles in a triangle total 180° , so the missing angle is equal to:
180 - (70+55)=55° .
2Recognise the other properties of the triangle.
As two angles are the same length, the missing side must be equal to 7cm . The triangle also has one line of symmetry (vertical) and no rotational symmetry.
The polygon is an isosceles triangle.
Example 2: multiple triangles
Two congruent, isosceles triangles are joined to form another triangle.
Use the information in the diagram below to classify the triangle ABD :
Determine the size of the angles/side lengths within the triangle.
As ACD is an isosceles, the angle CAD = 45° .
The angle ACD therefore equals 180 - (45 + 45) = 90° .
As the triangles are congruent, angle BCD = 90° and the angles CBA and CAB = 45° .
This means the angle BAD = 45 + 45 = 90° .
Recognise the other properties of the polygon.
As the angles BCD and ACD are both equal to 90° , BCD is a straight line.
The triangle ABD contains the three angles 90°, 45° and 45° so the triangle ABD is a right-angled isosceles triangle.
Example 3: exterior angles
The exterior angles of a triangle are equal to 110°, 120° and 130° .
Classify the triangle.
Determine the size of the angles/side lengths within the triangle.
As the sum of the interior and exterior angle at a vertex totals 180° , the interior angles are equal to:
180 - 110 = 70°
180 - 120 = 60°
180 - 130 = 50°
Recognise the other properties of the polygon.
As all three angles in the triangle are different and so all sides are different lengths, the triangle is a scalene triangle.
Example 4: algebraic
Three interior angles of a triangle are given as 2x+11, 3x+18 and x+31 .
Use this to determine the classification of the triangle.
Determine the size of the angles/side lengths within the triangle.
As the sum of angles in a triangle total 180° ,
2x+11+3x+18+x+31=180
6x+60=180
6x=120
x=20
As x=20
2x+11=2(20)+11=51°
3x+18=3(20)+18=78°
x+31=20+31=51°
Recognise the other properties of the polygon.
As two angles are equal, the triangle is an isosceles triangle.
Example 5: description
Three people stood at different points in a field, each with a compass. The bearing of person B from person A is 120° . The bearing of person C from person B is 240° . Person C is standing directly south of person A .
If each person stood at the vertex of a triangle, what classification of triangle would they produce?
Determine the size of the angles/side lengths within the triangle.
Drawing a sketch of the information above we have:
We can therefore find the three interior angles of the triangle ABC .
The interior angle at A = 180 - 120 = 60° (angles on a straight line total 180°).
The back bearing of A from B is equal to 180 - 120 = 60° (co-interior angles in parallel lines total 180° ).
This means the interior angle at B = 360 - (240 + 60) = 60° (angles at a point total 360° ).
The final angle at C can be calculated using the sum of angles in a triangle: 180 - (60 + 60) = 60° .
Recognise the other properties of the polygon.
As all three angles are equal to 60° , the triangle is an equilateral triangle.
Example 6: inscribed in a circle
The triangle ABC is inscribed in a circle.
Classify the triangle OBC .
Determine the size of the angles/side lengths within the triangle.
As the angle at the centre is twice the angle at the circumference, the angle BOC = 46×2 = 92° .
Recognise the other properties of the polygon.
OB and OC are radii of the circle and so triangle OBC is an isosceles triangle.
Common misconceptions
- Angles in polygons
Make sure you know your angle properties. Getting these confused causes quite a few misconceptions.
- Angles in a triangle total 180°.
- Angles in a quadrilateral total 360°.
- Angles on a straight line total 180°.
- Incorrect assumptions for triangles
Assuming a triangle is isosceles or equilateral can have an impact on the size of angles within the rest of the polygon, so make sure you can explain why you have chosen a specific type of triangle.
As well as this, stating that the polygon is a triangle is not enough information for a classification. You must state whether it is isosceles/ equilateral etc.
Practice types of triangles questions
1. Classify the following triangle.
Isosceles triangle

Scalene triangle

Right angle isosceles triangle

Right angle triangle

180 – (52 + 38) = 90^{\circ} (angles in a triangle total 180^{\circ} )
2. Use the information in the diagram to determine the type of triangle of ABD .
Right angle isosceles triangle

Isosceles trapezium

Scalene triangle

Equilateral triangle

BCD = 180 – (110+40) = 30^{\circ} (angles in a triangle total 180^{\circ} )
ADB = 180 – (75 + 30 + 40) = 35^{\circ} (angles in a triangle total 180^{\circ} )
ABD = 180 – 110 = 70^{\circ} (angles on a straight line total 180^{\circ} )
All three angles in triangle ABD are different. This is a scalene triangle.
3. The exterior angles of a triangle are equal to 120^{\circ} each. Classify the triangle.
Equilateral triangle

Isosceles triangle

Scalene triangle

Right angle isosceles triangle

As all the exterior angles are equal, the interior angles are also equal at
180 – 120 = 60^{\circ} .
4. Three interior angles of a triangle are given as 7x+21, 3x+12, and 2x+15 . Use this to determine the classification of the triangle.
Equilateral triangle

Isosceles triangle

Scalene triangle

Right angle triangle

As the sum of angles in a triangle total 180^{\circ} ,
7x+21+3x+12+2x+15=180\\ 12x+48=180\\ 12x=132\\ x=11As x=11
7x+21=7(11)+21=98^{\circ}\\
3x+12=3(11)+12=45^{\circ}\\
2x+15=2(11)+15=37^{\circ}
5. A plane travels on a bearing of 105^{\circ} from point A , then at a bearing of 140^{\circ} from point B . The plane lands at point C . The point C is at a bearing of 137^{\circ} from point A . Classify the triangle made between points A, B, and C .
Right angle isosceles triangle

Scalene triangle

Isosceles triangle

Right angle triangle

Angle BAC = 137 – 105 = 32^{\circ}
The back bearing at B = 180 – 105 = 75^{\circ}
Angle ABC = 360 – (170 + 75) = 115^{\circ} (angles at a point total 360^{\circ} )
Angle BCA = 180 – (115+32)=33^{\circ} (angles in a triangle total 180^{\circ} )
6. Use circle theorems to classify the triangle ABD .
Isosceles triangle

Equilateral triangle

Scalene triangle

Right angle triangle

Two tangents that meet the circumference of a circle are the same length, so
AB = AD . This means that ABD is an isosceles triangle.
Types of triangles GCSE questions
1.
(a) Below is a grid with three coordinates plotted.
What type of triangle is ABC ?
(b) Use the grid to find the coordinate of the centre of the polygon.
(3 marks)
(a)
Isosceles triangle
(1)
(b)
(1)
(3,3)
(1)
2.
(a) The rectangle ABCD and the triangle ADE are joined together as shown below. The lines AB and CE are parallel. Show that triangle ADE is a right angle isosceles triangle.
(b) The line AC is joined to create a new triangle ACE with angle BAC = 42^{\circ} . Calculate the size of angle EAC . Explain your working.
(7 marks)
(a)
As AB and CE are parallel, angle ADE = 90^{\circ}
(1)
Angle DAE = 180 – (90+45) = 45^{\circ}
(1)
Angle DEA = angle DAE so the triangle is isosceles and Angle ADE is a right angle
(1)
(b)
Angles BAC and ACD are alternate angles in parallel lines which are equal
(1)
Angle ACE = 42^{\circ}
(1)
Angle EAC = 180 – (45+42) = 93^{\circ}
(1)
Angles in a triangle total 180^{\circ}
(1)
3.
(a) An isosceles triangle ABC contains the angle 50^{\circ} . Work out the possible sizes for the other two angles.
(b) A different isosceles triangle PQR is inscribed in a circle. The points P and R are connected to the centre of the circle to form a further triangle POR . What type of triangle is POR ? Explain your answer.
(6 marks)
(a)
(180 -50)\div2 = 65^{\circ}
(1)
65^{\circ} and 65^{\circ}
(1)
180 – (50+50) = 80^{\circ}
(1)
50^{\circ} and 80^{\circ}
(1)
(b)
Isosceles triangle
(1)
OP and OR are radii and so are the same length
(1)
Learning checklist
You have now learned how to:
- Plot specified points and draw sides to complete a given polygon. Distinguish between regular and irregular polygons based on reasoning about equal sides and angles
- Compare and classify geometric shapes based on their properties and sizes and find unknown angles in any triangles, quadrilaterals, and regular polygons
- Describe, sketch and draw using conventional terms and notations: points, lines, parallel lines, perpendicular lines, right angles, regular polygons, and other polygons that are reflectively and rotationally symmetric
- Derive and use the sum of angles in a triangle and use it to deduce the angle sum in any polygon, and to derive properties of regular polygons
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.