GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
2D shapes Lines of symmetry Rotational symmetry Types of angles Angles in a triangle How to work out perimeterThis topic is relevant for:

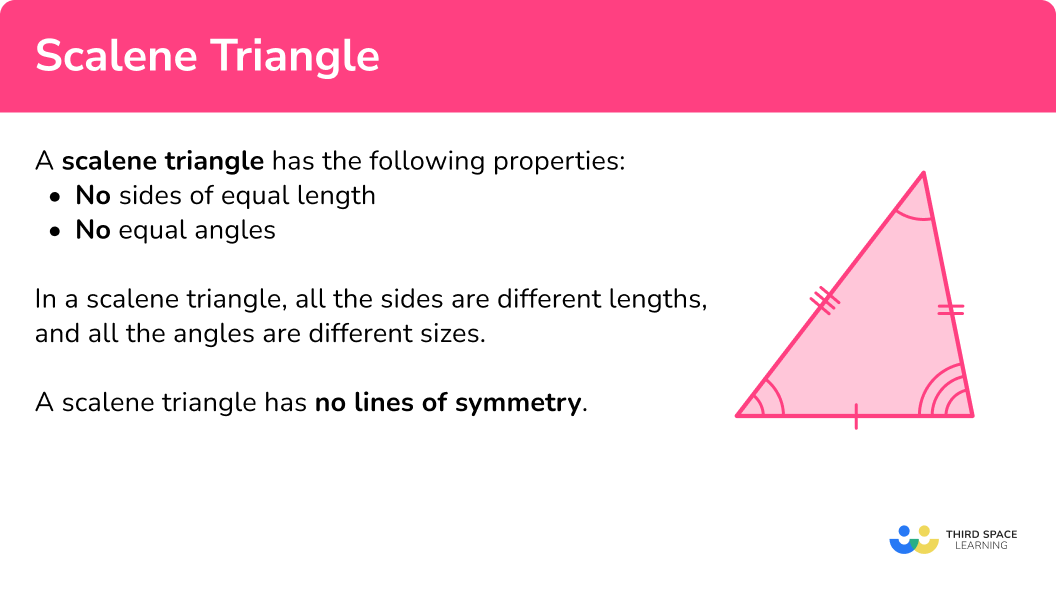
Scalene Triangle
Here we will learn about scalene triangles, including what a scalene triangle is and how to solve problems involving their sides and their angles.
There are also scalene triangles worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is a scalene triangle?
A scalene triangle is a type of triangle that has the following properties,
- No equal sides.
- No equal angles.

A scalene triangle with an obtuse angle is a type of obtuse triangle sometimes known as an obtuse scalene triangle.
A scalene triangle which has three acute angles is a type of acute triangle which is sometimes known as an acute scalene triangle.

Properties of triangles are very important within geometry.
They are one of the most common shapes to recognise for angles in parallel lines, circle theorems, interior angles, trigonometry, Pythagoras’ theorem and many more.
It is therefore important to be familiar with their individual properties.
What is a scalene triangle?
Scalene right-angled triangle
If one of the angles of a scalene triangle is a right-angle, the triangle can be called a right-angled triangle or a right triangle.

Symmetry
A scalene triangle has no lines of symmetry.
It can be said that a scalene triangle has order of rotational symmetry \bf{1} as it looks the same once in a full turn.
Area of a scalene triangle
The area of a scalene triangle can be found by using the formula
A=\cfrac{1}{2} \, bh,
where b is the length of the base of the triangle and h is the perpendicular height of the triangle. Sometimes these values need to be calculated.
For example, to calculate the area of the scalene triangle below, we need to know the value for the base b, and the value of the perpendicular height h.
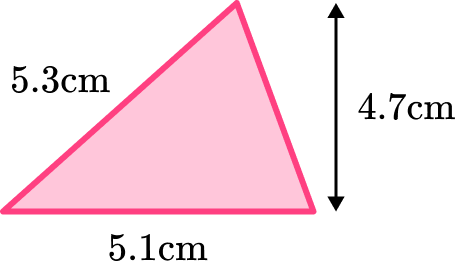
Here b=5.1 \, cm and h=4.7 \, cm. The value of 5.3 \, cm can be confusing when calculating the area of a triangle as it is not the height of the triangle, it is another side length, so beware!
Substituting the values for b and h into the area formula, we have
A=\cfrac{1}{2} \, bh=\cfrac{1}{2} \, \times{5.1}\times{4.7}=11.985\text{ cm}^{2}.
Remember that an area uses square units.
Step-by-step guide: Area of a triangle
How to solve problems involving scalene triangles
In order to solve problems involving scalene triangles:
- Locate known angles and calculate any necessary unknown angles.
- Locate known sides and calculate any necessary unknown side lengths.
- Solve the problem using any necessary values.
How to solve problems involving scalene triangles

Types of triangles worksheet (includes scalene triangle)

Get your free scalene triangle worksheet of 20+ types of triangles questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Types of triangles worksheet (includes scalene triangle)

Get your free scalene triangle worksheet of 20+ types of triangles questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on triangles
Scalene triangle is part of our series of lessons to support revision on polygons and triangles. You may find it helpful to start with the main triangles lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Scalene triangle examples
Example 1: finding the missing angle of a scalene triangle
Determine the size of angle x.

- Locate known angles and calculate any necessary unknown angles.
We know two of the three angles, with the third angle being the value we need to calculate, x.
2Locate known sides and calculate any necessary unknown side lengths.
As the problem requires us to calculate a missing angle and we know two of the three angles in the triangle, we do not need to use any side lengths to solve the problem, so we do not need to calculate any of these.
3Solve the problem using any necessary values.
As the sum of angles in a triangle is 180^{\circ}, we can calculate the missing value of x by subtracting the other two angles from 180.
180-(95+63)=22^{\circ}
The angle x=22^{\circ}.
Example 2: finding the missing angle inside parallel lines
Triangle BEF lies between two parallel lines AC and DG.
The vertices at E and F lie on the line DG, angle CBF = 53^{\circ} and angle EBF = 90^{\circ}.
Determine the size of angle BEF.
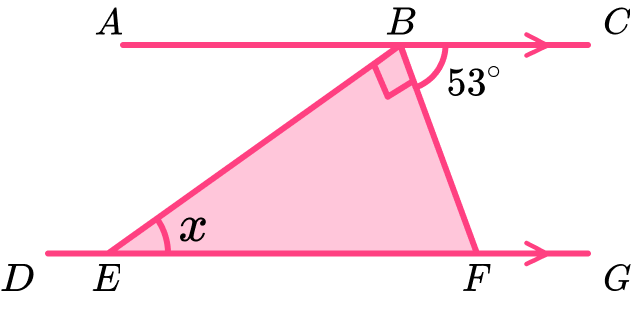
Locate known angles and calculate any necessary unknown angles.
The angle x lies within a triangle.
If we know the other two angles within the triangle then we can use the angle fact that the sum of angles in a triangle is 180^{\circ} to determine the size of angle x.
The angle EBF = 90^{\circ}. This means we need to determine the size of angle BFE next.
Alternate angles in parallel lines are equal and angle CBF is alternate to the angle BFE, so the angle BFE = 53^{\circ}.
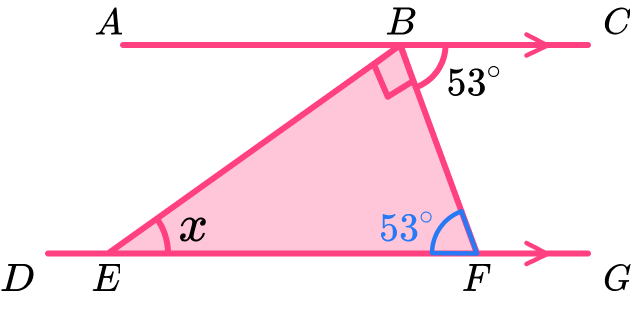
Locate known sides and calculate any necessary unknown side lengths.
As the problem requires us to calculate a missing angle and we know two of the three angles in the triangle, we do not need to use any side lengths to solve the problem, so we do not need to calculate any of these.
Solve the problem using any necessary values.
As the sum of angles in a triangle is 180^{\circ}, we can calculate the missing value of x by subtracting the other two angles from 180.
180-(90+53)=37^{\circ}
The angle x=37^{\circ}.
Example 3: reverse perimeter of a scalene triangle problem
The perimeter of the triangle is 95.6 \, cm. Find the length of the missing side PQ.
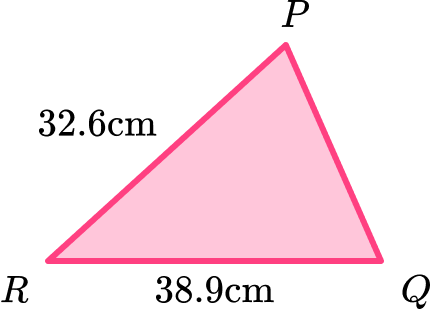
Locate known angles and calculate any necessary unknown angles.
We do not know any of the angles in the triangle and as this question relates to the perimeter, which is a measure of length, we do not need to determine the size of any of the angles for this problem.
Locate known sides and calculate any necessary unknown side lengths.
We know the two side lengths PR = 32.6 \, cm and QR = 38.9 \, cm.
The unknown side length PQ is what we need to find the length of.
Solve the problem using any necessary values.
Subtracting the sum of the other two sides from the perimeter will give us the missing side length PQ.
95.6-(32.6+38.9)=24.1\text{ cm}
The missing side length PQ = 24.1 \, cm.
Example 4: perimeter of a scalene triangle problem involving ratio
The perimeter of the triangle is 72 \, cm.
The ratio of the sides is 2:3:4.
Find the length of the longest side.
Locate known angles and calculate any necessary unknown angles.
We currently do not know the size of any of the angles in the triangle, however the problem involves the perimeter, which is a measure of length, so we do not need to calculate these values.
Locate known sides and calculate any necessary unknown side lengths.
As the perimeter is 72 \, cm in the ratio of 2:3:4, we need to work out the scale factor of enlargement to get from the scaled triangle to the similar triangle.
By adding up the parts in the ratio, the perimeter of the scaled triangle is 2 + 3 + 4 = 9 \, cm.
As the similar triangle has a perimeter of 72 \, cm, we need to divide these two values to get the scale factor of enlargement.
72\div{9}=8
This means that each side length is 8 times greater than the scaled triangle. Multiplying each part of the ratio by 8, we have the new side lengths,
2\times{8}=16\text{ cm}
3\times{8}=24\text{ cm}
4\times{8}=32\text{ cm}
The three side lengths of the similar triangle are 16 \, cm, 24 \, cm, and 32 \, cm.
Solve the problem using any necessary values.
As we need the longest side of the triangle, this is 32 \, cm.
Note: This method is the same as when we divide a quantity into a ratio where we have the quantity 72 \, cm, and the ratio 2:3:4.
Example 5: compound scalene triangles
Two congruent scalene triangles produce the compound shape ABCD where AC is a line of symmetry. Determine the size of angle BAD.
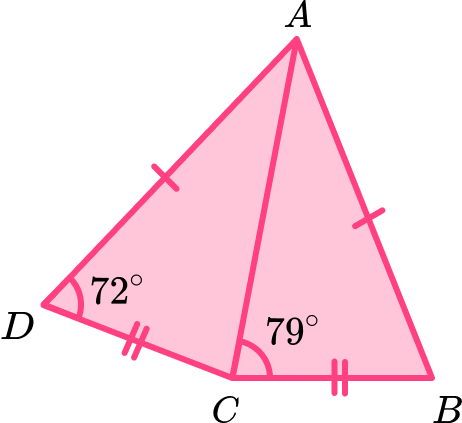
Locate known angles and calculate any necessary unknown angles.
We know that angle ADC = 72^{\circ} and angle ACB = 79^{\circ}.
AC is a line of symmetry, so we can state that the angle ACD = 79^{\circ} as this is the other side of the line of symmetry at C.
This means that we have two of the three angles in the triangle ACD.
Using the fact that the sum of angles in a triangle total 180^{\circ}, the third angle CAD is equal to 180-(72+79)=29^{\circ}.
We now have the angles in the scalene triangle ACD.
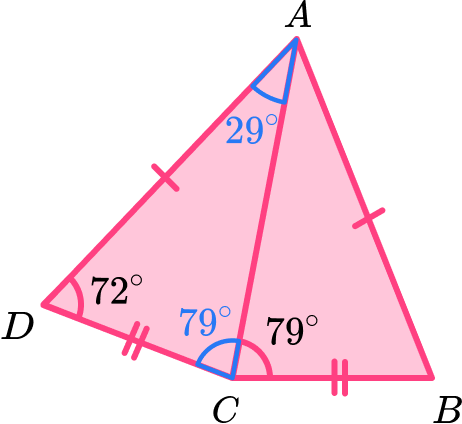
Locate known sides and calculate any necessary unknown side lengths.
This question does not involve side lengths as we are calculating an internal angle and so we do not need to calculate any of these values.
Solve the problem using any necessary values.
Now we know that the angle CAD = 29^{\circ}, the angle BAC is equal to angle CAD as AC is a line of symmetry, so angle BAC = 29^{\circ}.
As we want to calculate the angle BAD, we need to add angle CAD and BAC together.
29+29=58^{\circ}
Angle BAD = 58^{\circ}
Example 6: calculating a missing side length of a scalene triangle problem involving ratio
Triangle ABC is made from two right-angled scalene triangles that meet at the line BM. \; M is a point on the line AC such that AM : AC = 2 : 7.
Given that MC = 20 \, cm, calculate the length of side BC, labelled x.
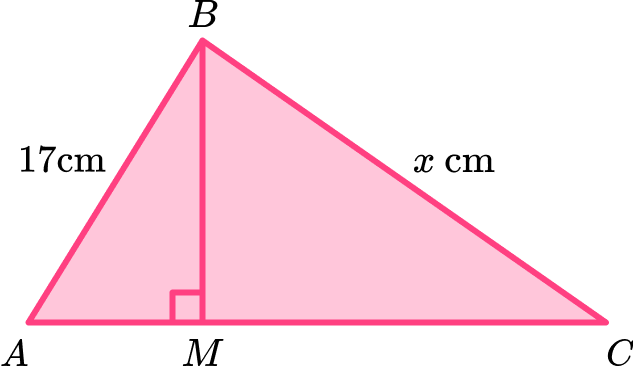
Locate known angles and calculate any necessary unknown angles.
We can see that the angle AMB is a right-angle, which is also the same for angle BMC as AC is a straight line.
We do not know any further angles in either triangle, so we will need to work with the side lengths to solve this problem.
Locate known sides and calculate any necessary unknown side lengths.
In order to find the length of the side BC, we need to use Pythagoras’ theorem.
However, we do not know the height, BM, of the triangle BCM, so we need to calculate this first.
In order to calculate the missing height, BM, we can use Pythagoras’ theorem but we can only do this once we know the length of the side AM.
As AM : AC = 2 : 7, this is a part to whole ratio and so we can state that the length AM is \, \cfrac{2}{7} \, of the length AC and the length MC is \, \cfrac{5}{7} \, of the length AC.
As MC = 20 \, cm, we can divide 20 by \, \cfrac{5}{7} \, to calculate the length of A.
20\div\cfrac{5}{7}=20\times\cfrac{7}{5}=28\text{ cm}
As AC = 28 \, cm, we can quickly subtract the length of MC from AC to get the length of AM.
AM =28-20=8\text{ cm}
This gives us
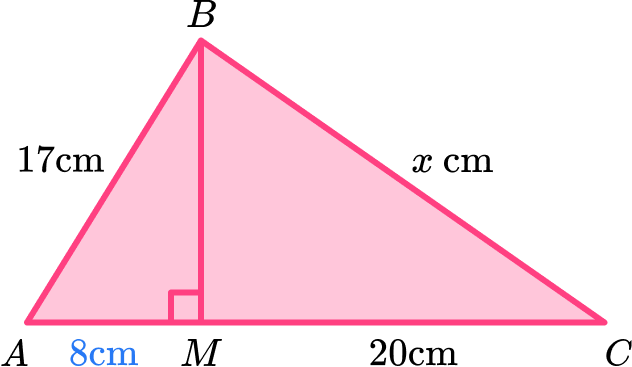
Solve the problem using any necessary values.
Using Pythagoras’ theorem to find the length of BM in the triangle ABM, we have
BM=\sqrt{c^{2}-b^{2}}=\sqrt{17^{2}-8^{2}}=15\text{ cm}
So, BM = 15 \, cm.
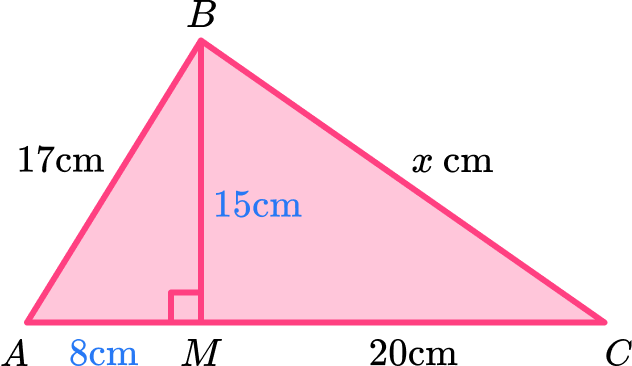
Using Pythagoras’ theorem again to calculate the missing length BC of triangle BCM, we have
BC=\sqrt{a^{2}+b^{2}}=\sqrt{15^{2}+20^{2}}=25\text{ cm}
This gives us the length BC = 25 \, cm.
Common misconceptions
- Angles in polygons
Make sure you know your angle properties. Getting these confused causes quite a few misconceptions.
∘ Angles in a triangle total 180^{\circ}.
∘ Angles in a quadrilateral total 360^{\circ}.
- Angle facts
Make sure you know your angle facts.
∘ Adjacent angles on a straight line add up to 180^{\circ}.
∘ Vertically opposite angles are equal.
∘ Alternate angles are equal.
∘ Corresponding angles are equal.
Practice scalene triangle questions
1. Which of these triangles is a scalene triangle?
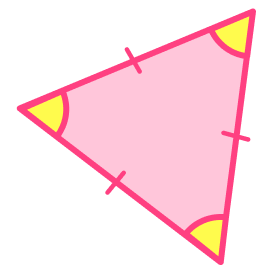






A scalene triangle has no equal sides and no equal angles. The other triangles have equal sides and equal angles, so they are not scalene triangles.
2. How many lines of symmetry does a scalene triangle have?




As a scalene triangle has no equal sides or equal angles, if we introduced a line of symmetry, this would mean that either two sides must be the same length, or two angles are the same size (as one is a reflection of the other).
This is true through any vertex or side length of the triangle and so a scalene triangle has 0 lines of symmetry.
3. What is the order of rotational symmetry of a scalene triangle?


No rotational symmetry


A scalene triangle only looks the same once in a full turn.
It therefore has order of rotational symmetry of 1, also described as having no rotational symmetry.
4. Determine the size of the missing interior angle in the triangle below.
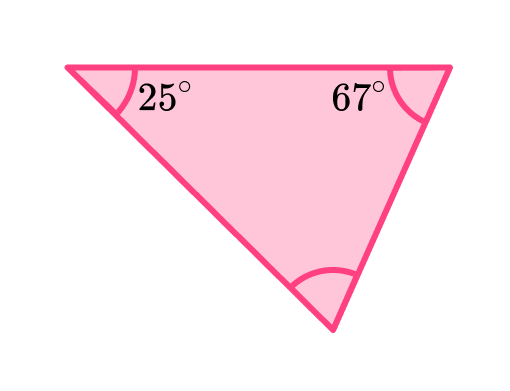




The sum of interior angles of a triangle is 180^{\circ}.
We can subtract the other two angles to find the missing angle.
180-(67+25)=88^{\circ}
The missing angle is 88^{\circ}.
5. Find the value of the unknown angle x.
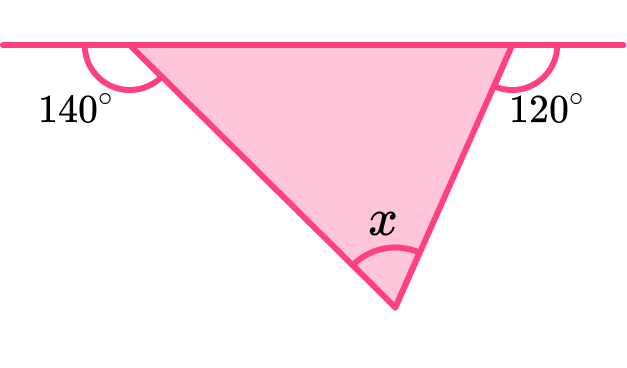




The sum of adjacent angles on a straight line is 180^{\circ}.
We can use this to find two angles in the triangle.
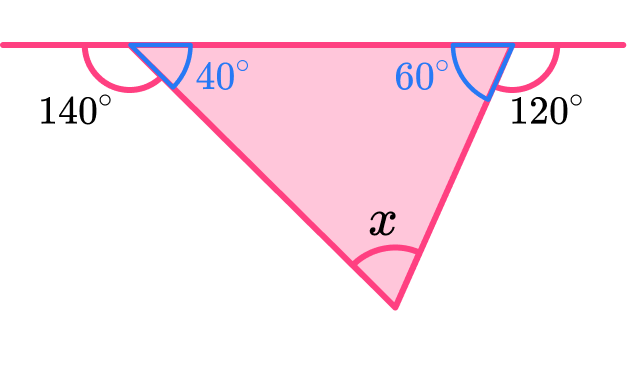
180-140=40^{\circ}
180-120=60^{\circ}
We can find the third angle of the triangle by using the fact that angles in a triangle sum to 180^{\circ}.
180-(40+60)=80^{\circ}
The missing angle is 80^{\circ}.
6. The perimeter of a triangle is 45 \, cm.
The ratio of the sides of the triangle is 4:6:5.
Find the length of the shortest side.




The sum of the parts of the ratio is 4+6+5=15.
We then divide the perimeter by the sum of the parts of the ratio 45\div 15=3.
We can then multiply the smallest part of the ratio by 3 to find the length of this side 4\times 3=12 .
The shortest side is 12 \, cm.
Scalene triangle GCSE questions
1. The triangle below is drawn accurately.

Circle the type of triangle it is.
Isosceles \hspace{0.5cm} Scalene \hspace{0.5cm} Equilateral \hspace{0.5cm} Right-angled
(1 mark)
Scalene
(1)
2. (a) Write down the coordinates of point A.
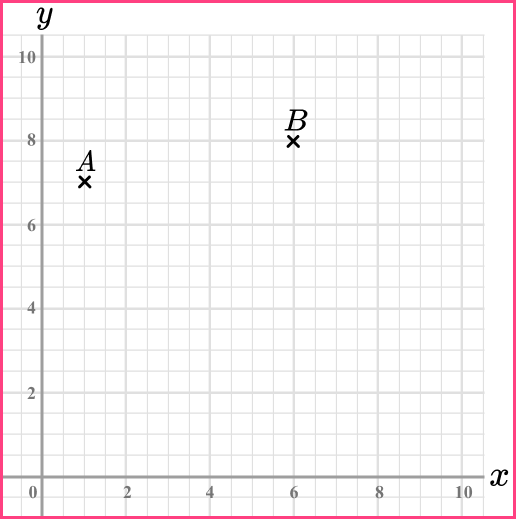
(b) Plot the point (8,1) and label it C.
(c) The points A, B and C make a triangle.
Write down the type of triangle ABC is.
(d) Triangle ABC is enlarged about the origin by a scale factor of 2, creating the image A’B’C’.
Determine the length of A’B’. Write your answer as a surd in the simplest form.
(7 marks)
(a) (1,7)
(1)
(b)
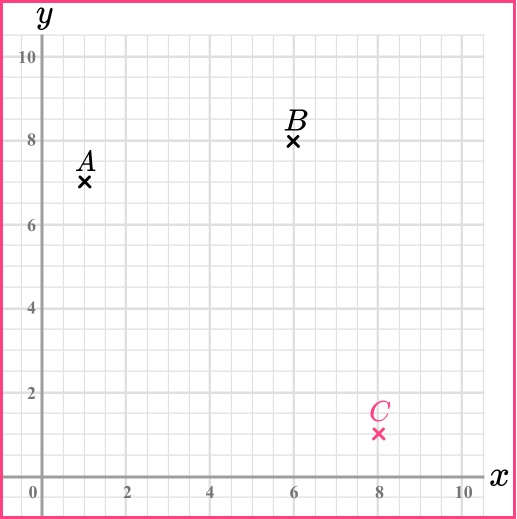
(1)
(c) Scalene
(1)
(d)
y_2-y_1=8-7=1
(1)
x_2-x_1=6-1=5
(1)
AB = \sqrt{1^2+5^2}=\sqrt{26}
(1)
\sqrt{26} \times 2=2 \sqrt{26}
(1)
Alternate Method
A'(2,14) and B'(12,16)
y_2-y_1=16-14=2
(1)
x_2-x_1=12-2=10
(1)
AB = \sqrt{2^2+10^2}=\sqrt{104}
(1)
\sqrt{104}=\sqrt{4 \times 26}=2 \sqrt{26}
(1)
3. (a) Triangle ABC has a perimeter 32.8 \, cm.
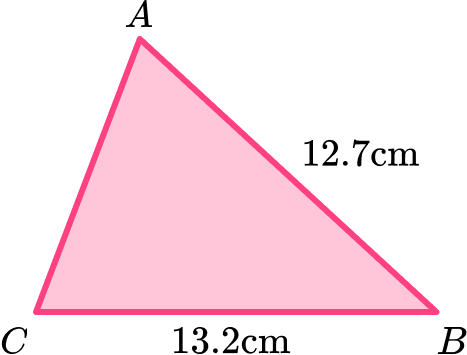
Find the length of AC .
(b) Heron’s formula is used to find the area of a triangle.
Heron’s formula is Area=\sqrt{s(s-a)(s-b)(s-c)} where s is half the perimeter and a, b and c are the lengths of the sides.
Use Heron’s formula to find the area of the triangle ABC.
Give your answer to 1 decimal place.
State the units for your answer.
(6 marks)
(a)
32.8-12.7-13.2 <?p>
(1)
6.9 \, cm
(1)
(b)
s=32.8 \div 2=16.4
(1)
Area=\sqrt{16.4(16.4-6.9)(16.4-13.2)(16.4-12.7)}=44.9496…
(1)
=44.9
(1)
cm^2
(1)
Learning checklist
You have now learned how to:
- Recognise a scalene triangle
- Use the properties of a scalene triangle to solve problems
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.