GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
Solving quadratic equations by factorising Quadratic formula Quadratic graphs Inequalities on a number lineThis topic is relevant for:

Quadratic Inequalities
Here we will learn about quadratic inequalities including how to solve quadratic inequalities, identify solution sets using inequality notation and represent solutions on a number line.
There are also quadratic inequalities worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are quadratic inequalities?
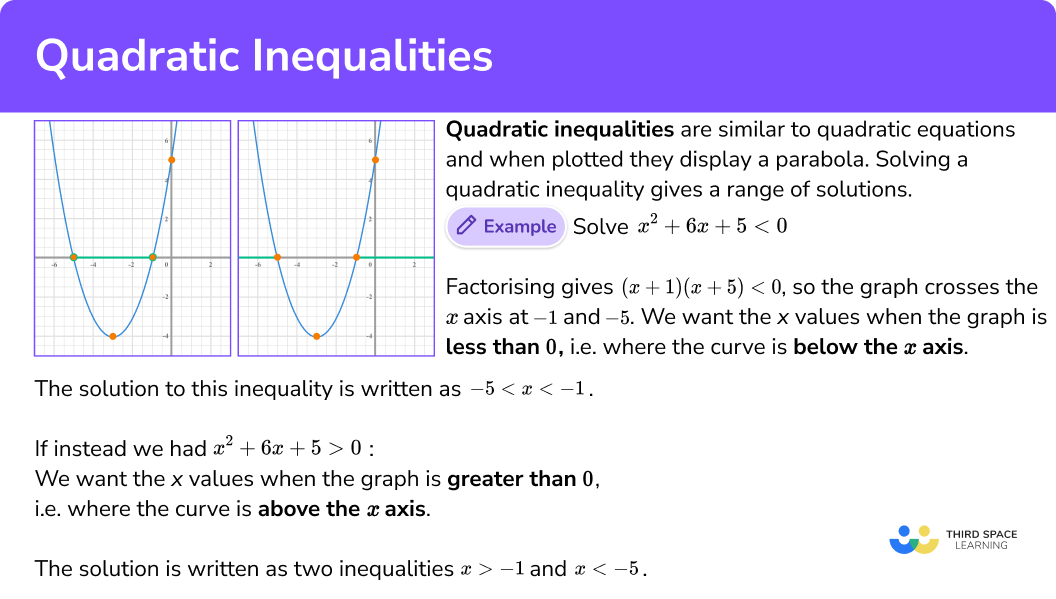
Quadratic inequalities are similar to quadratic equations and when plotted they display a parabola. We can solve quadratic inequalities to give a range of solutions.
For example,
The quadratic equation x^{2}+ 6x +5 = 0 has two solutions.
This is shown on the graph below where the parabola crosses the x axis.
We could solve this by factorising: (x + 1)(x + 5) = 0 .
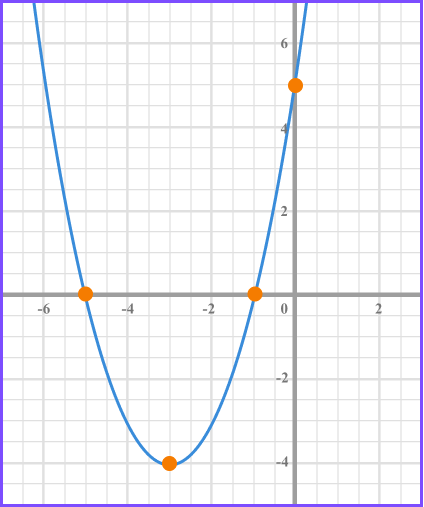
The two values of x that equate this equation to zero are x = - 1 and x = - 5 .
For example,
The quadratic inequality x^{2}+ 6x +5 \leq 0 can be solved by factorising but instead of two solutions, there are a range of solutions.
x^{2}+ 6x +5 \leq 0 means that the we need to know the x values that when the graph is less than 0 .
This corresponds to where the curve is below the x axis.
We can see the from the graph that the x values need to be between -1 and -5 .
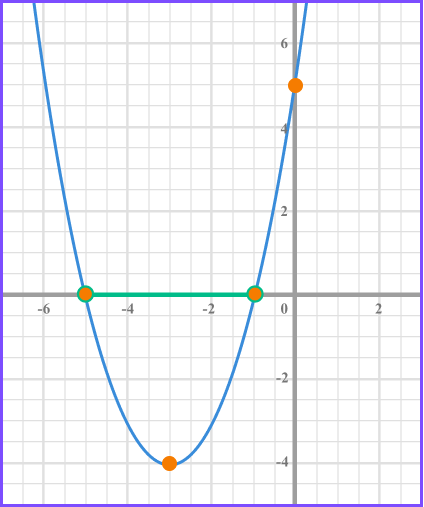
Therefore the solution to this inequality can be written using inequality notation,
-5\leq x \leq-1 .
For example,
The quadratic inequality x^{2} + 6x +5 > 0 is similar to the previous inequality and has a range of solutions.
x^{2}+ 6x +5 > 0 means that we need to know the x values when the graph is greater than 0 .
This corresponds to where the curve is above the x axis.
We can see the from the graph that the x values need to be greater than -1 and less than -5 .
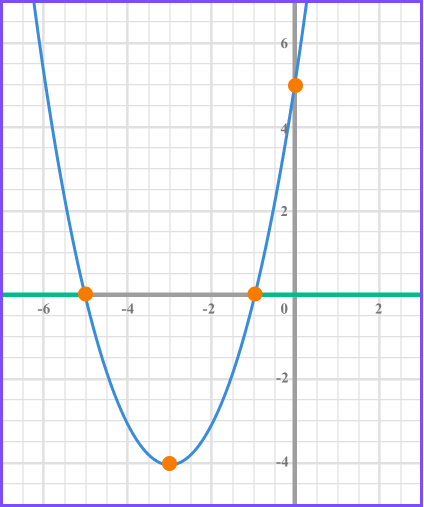
Therefore the solution to this inequality can be written using inequality notation as two inequalities x > -1 or x < -5 .
What are quadratic inequalities?
How to solve quadratic inequalities
In order to solve quadratic inequalities by factorising:
- Factorise the quadratic expression.
- Find the values of x that make each bracket equal zero.
- Write the solution using inequality notation.
In order to solve quadratic inequalities by using the quadratic formula:
- Identify values of a, b and c to substitute into the quadratic formula.
- Solve the quadratic inequality using the quadratic formula.
- Simplify to calculate the solutions of the inequality.
- Write the solution using inequality notation.
How to solve quadratic inequalities by factorising

How to solve quadratic inequalities by using the quadratic formula


Quadratic inequalities worksheet

Get your free quadratic inequalities worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Quadratic inequalities worksheet

Get your free quadratic inequalities worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on inequalities
Quadratic inequalities is part of our series of lessons to support revision on inequalities. You may find it helpful to start with the main inequalities lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Quadratic inequalities examples
Example 1: solving by factorising
Solve x ^{2}+7x+10 < 0 .
- Factorise the quadratic expression.
2Find the values of x that make each bracket equal zero.
(x + 2) = 0 when x = -2
(x + 5) = 0 when x = -5
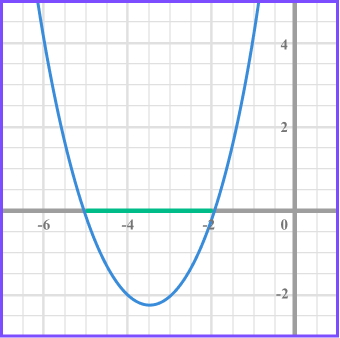
3Write the solution using inequality notation.
We need the values of x that produce a graph that is less than 0 and so below the x axis.
The inequality is given by -5 < x < -2 .
4Represent the solution set on a number line.
-5 and -2 are not included in the solution set so these values are indicated with open circles.
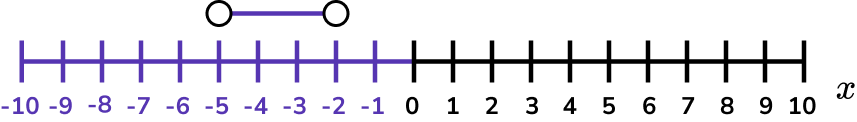
Example 2: solving by factorising
Solve x^{2}+3x+10\leq0 .
Factorise the quadratic expression.
Find the values of x that make each bracket equal zero.
(x - 2) = 0 when x = 2
(x + 5) = 0 when x = -5
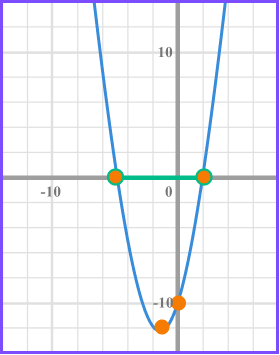
Write the solution using inequality notation.
We need the values of x that produce a graph that is less than or equal to 0 and so below the x axis.
The inequality is given by -5\leq x \leq2 .
Represent the solution set on a number line.
-5 and 2 are included in the solution set so these values are indicated with closed circles.

Example 3: solving by factorising
Solve x^{2}-6x+8\geq0 .
Factorise the quadratic expression.
Find the values of x that make each bracket equal zero.
(x -2) = 0 when x = 2
(x -4 ) = 0 when x = 4
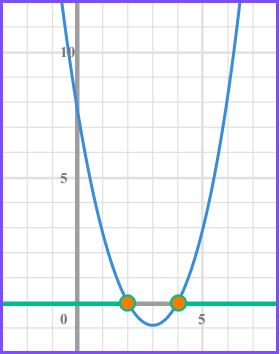
Write the solution using inequality notation.
We need the values of x that produce a graph that is greater than or equal to 0 and so above the x axis.
There will be two separate inequalities as there are two separate regions indicated on the graph.
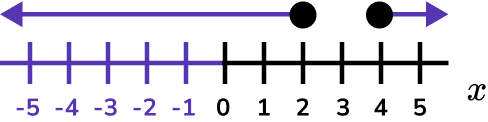
x \geq4 and x \leq2 .
Represent the solution set on a number line.
2 and 4 are included in the solution set so these values are indicated with closed circles.
Example 4: solving by factorising
List the integers that satisfy 2x^{2} + 9x + 4\leq0
Factorise the quadratic expression.
Find the values of x that make each bracket equal zero.
(2x + 1) = 0 when x = -\frac{1}{2}
(x +4 ) = 0 when x = -4
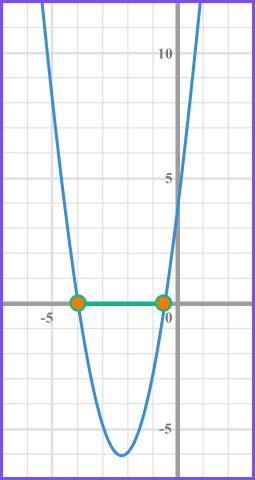
Write the solution using inequality notation.
We need the values of x that produce a graph that is less than or equal to 0 and so below the x axis.
The inequality is given by -4\leq x \leq-\frac{1}{2} .
List the integer values that are included in the solution set.
x is any value greater than or equal to -4 and less than or equal to -\frac{1}{2} . The highest integer below -\frac{1}{2} is -1 .
Example 5: solving by factorising
Solve x^{2}-9>0 .
Factorise the quadratic expression.
Find the values of x that make each bracket equal zero.
(x +3) = 0 when x = -3
(x -3 ) = 0 when x = 3
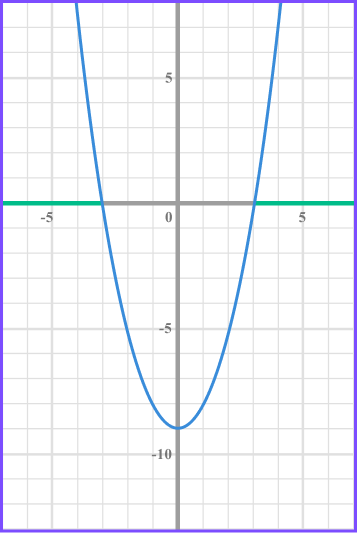
Write the solution using inequality notation.
We need the values of x that produce a graph that is greater than 0 and so above the x axis.
There will be two separate inequalities as there are two separate regions indicated on the graph.
x>3 and x < -3 .
Represent the solution set on a number line.
-3 and 3 are not included in the solution set so these values are indicated with closed circles.
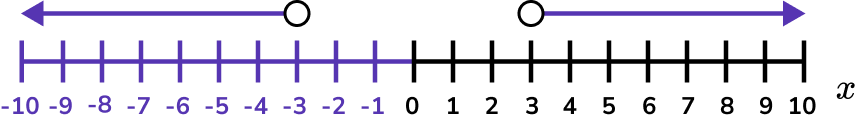
Example 6: solving by factorising and rearranging
List the integers that satisfy x^{2}<16 .
Rearrange the inequality.
Rearrange the inequality so that it is less than 0 by subtracting 16 from both sides.
x^{2}-16< 0Factorise the inequality.
Find the values of x that make each bracket equal zero.
(x +4) = 0 when x = -4
(x -4 ) = 0 when x = 4
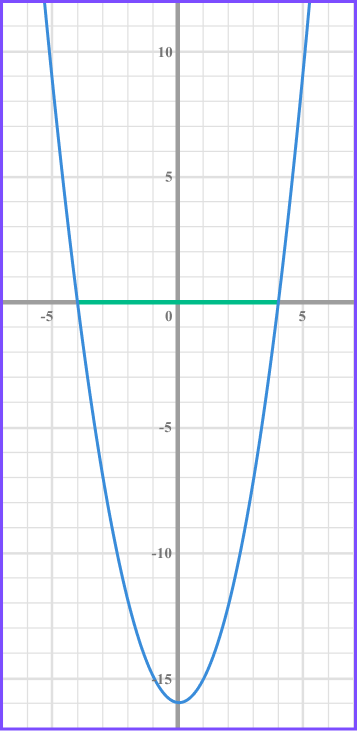
Write the solution using inequality notation.
We need the values of x that produce a graph that is less than 0 and so below the x axis.
The inequality is given by -4 < x < 4 .
List the integer values that are included in the solution set.
x is any value greater than -4 and less than 4 .
Example 7: solving by using the quadratic formula
Solve 5x^{2}+6x-12\leq0 .
Identify values of a, b and c to substitute into the quadratic formula.
A quadratic expression is in the form ax^{2} + bx + c .
In this inequality a = 5, b = 6 and c = -12 .
Substitute the values into the quadratic formula.
The quadratic formula is x = \frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} .
Substituting the values a = 5, b = 6 and c = -12 gives x = \frac{-6 \pm \sqrt{6^{2}-4 \times 5 \times-12}}{2 \times 5} .
We need to use the quadratic formula to solve rather than factorising as the discriminant is not a square number.
Simplify to calculate the solutions of the inequality.
In this case the answer is given in surd form but you may be asked to leave the answers rounded to a degree of accuracy.
Write the solution using inequality notation.
We need the values of x that produce a graph that is less than or equal 0 and so below the x axis.
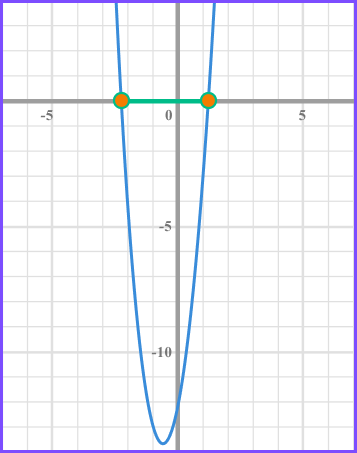
The inequality is given by \frac{-3- \sqrt{69}}{5} \leq x \leq \frac{-3+ \sqrt{69}}{5} .
Example 8: solving by using the quadratic formula
Solve 2x^{2}-3x- 4 < 0 .
Identify values of a, b and c to substitute into the quadratic formula.
A quadratic expression is in the form ax^{2}+bx+c .
In this inequality a = 2, b = -3 and c = -4 .
Substitute the values into the quadratic formula.
The quadratic formula is x = \frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} .
Substituting the values a = 2, b =-36 and c = -4 gives
x=\frac{-(-3) \pm \sqrt{(-3)^{2}-4 \times 2 \times-4}}{2 \times 2} .
Simplify to calculate the solutions of the inequality.
In this case the answer is being given to two decimal places but you could leave the solution in surd form.
Write the solution using inequality notation.
We need the values of x that produce a graph that is less than 0 and so below the x axis.
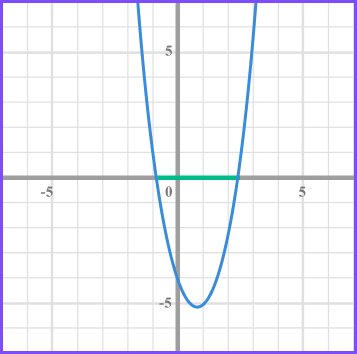
The inequality is given by -0.85 < x< 2.35 .
Rounded to two decimal places.
Example 9: one solution
Solve x^{2}+6x+9\leq0 .
Factorise the inequality.
(x + 3)(x + 3) \leq 0 or (x+3)^{2}
Find the values of x that make each bracket equal zero.
As both brackets are equal, there is only one solution.
(x +3) = 0 when x = -3
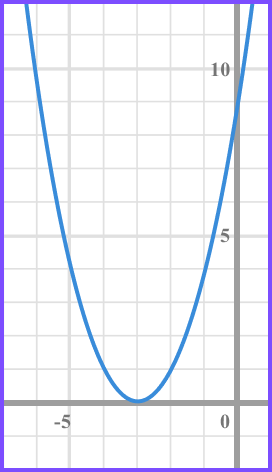
Write the solution using inequality notation.
We need the values of x that produce a graph that is less than or equal to 0 and so below the x axis. This only happens when, x = -3 .
Common misconceptions
- Square root of a number has two solutions
A common error when calculating the square root of a number is only writing the positive solution. A negative number squared will also give a positive solution.
For example,
When solving x^2=16, x=\pm \sqrt{16} =\pm 4 .
- Not maintaining the original inequality sign
A common error is to accidentally change the direction of the inequality sign or not writing an inequality sign in the solution.
- Writing a double inequality when the solution set is split
When solving x^{2} + 10x +16 < 0 there is one solution set which is below the x axis. Therefore the solution is -8 < x < -2 .
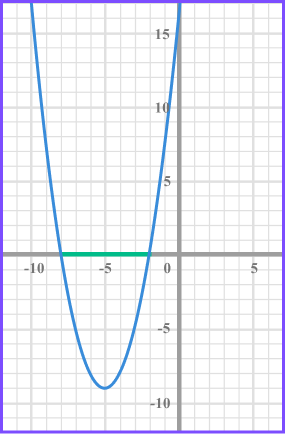
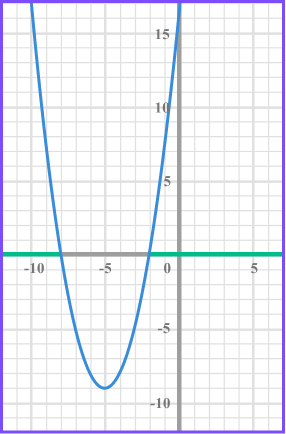
When solving x^{2} + 10x +16 > 0 there is one solution set which is above the x axis. Therefore the solution is x<-8 and x > -2 .
Practice quadratic inequalities questions
1. Solve x^{2}+13x+30<0 .


-10 and -3


Factorise the quadratic, (x + 3)(x +10) < 0 .
Find the values of x that make the bracket equal zero, x = -10 and x = -3 .
Write the solution using interval notation, -10 < x < -3 .
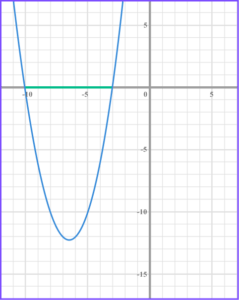
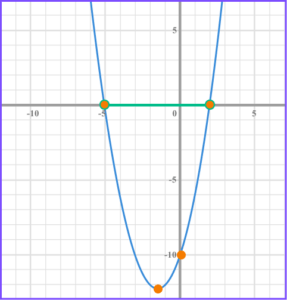
2. Solve x^{2}+3x-10\leq0 .


-5 and -2


Factorise the quadratic, (x + 5)(x -2) \leq 0 .
Find the values of x that make the bracket equal zero, x = -5 and x = 2 .
Write the solution using interval notation, -5\leq x \leq2 .
3. Solve x^{2}-7x+6\geq0 .



x \leq 1 and x\geq 6

Factorise the quadratic, (x-6)(x-1)\geq 0 .
Find the values of x that make the bracket equal zero, x = 6 and x =1 .
Write the solution using interval notation, x \leq 1 and x\geq6 .
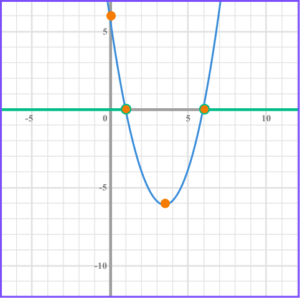
4. Solve 2x^{2}-11x+ 5 \leq 0 .




Factorise the quadratic, (2x-1)(x-5) \leq 0 .
Find the values of x that make the bracket equal zero, x =\frac{1}{2} and x =5 .
Write the solution using interval notation, \frac{1}{2} \leq x\leq 5 .
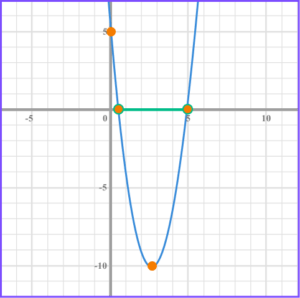
5. Solve x^{2}-25>0 .

x = -5 and x =5



Factorise the quadratic, (x + 5)(x -5) > 0 .
Find the values of x that make the bracket equal zero, x = -5 and x =5 .
Write the solution using interval notation, x < -5 and x > 5 .
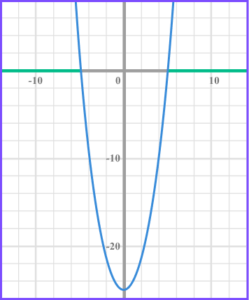
6. Solve x^{2}<1 .




Rearrange to make the inequality less than zero, x^{2} – 1<0 .
Factorise the quadratic, (x + 1)(x -5) < 0 .
Find the values of x that make the bracket equal zero, x = -1 and x =1 .
Write the solution using interval notation, -1 < x < 1 .
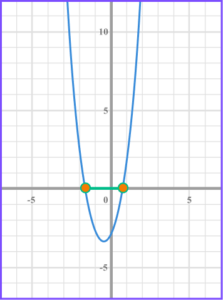
7. Solve 3x^{2}+4x-2\leq 0 .




3x^{2} + 4x – 2 \leq 0 .
Identify a, b and c from the form ax^{2} +bx + c \leq 0 , a = 3, b = 4, c = -2 .
Substitute the values in to the quadratic formula, x = \frac{-4 \pm \sqrt{4^{2}-4 \times 3 \times-2}}{2 \times 3} .
Simplify the inequality, x = \frac{-4 \pm \sqrt{16–24}}{6} .
Simplify further, x=\frac{-4 \pm \sqrt{40}}{6} .
You could simplify to surd form, x = \frac{-4 \pm 2 \sqrt{10}}{6} .
Simplify the fraction. You could leave in surd form, x = \frac{-2 \pm \sqrt{10}}{3} .
Correct to 2 decimal places, x \leq 0.39 and x \geq -1.72 .
Written in surd form written in interval notation, \frac{-2+\sqrt{10}}{3} \leq x \leq \frac{-2+\sqrt{10}}{3} .
Written as an inequality with values rounded to 2 decimal places, -1.72 \leq x \leq 0.39 .

8. Solve x^{2}-10x+25 \leq 0 .




x^{2} -10x +25 \leq 0 .
Factorise the quadratic, (x – 5)(x -5) \leq 0 .
Find the values of x that make the bracket equal zero, x =5 .
The quadratic only has one root at 5, so is never less than zero but equal to zero at 5, x = 5 .
Quadratic inequalities GCSE questions
1. Solve the inequality x^{2}-8x+15\leq 0 .
(4 marks)
Factorise the inequality. 1 mark if there are one or two errors.
(2)
Roots found x = 3 and x = 5
(1)
3\leq x \leq 5Correct answer.
(1)
2. (a) Find the interval for which x^{2}+3x – 10 < 0 .
(b) Represent your solution to part (a) on the number line below.

(6 marks)
(a)
(x -2)(x + 5) < 01 mark if there are one or two errors.
(2)
Roots found x =2 and x = -5
(1)
-5 < x < 2(1)
(b)
-5 and 2 indicated.
(1)
Correct solution with open circles.

(1)
3. Here is a rectangle.

All measurements are in centimetres.
x is an integer.
The total area of the rectangle is less than 21cm^{2} .
Show that 4 <x < 7 .
x^{2} – 4x <21 .
(1)
x^{2} – 4x – 21< 0 .
(1)
(x – 7)(x + 3) < 0 .
(1)
7 and -3
(1)
4<x < 7 as you cannot have a negative value for distance.
(1)
Learning checklist
You have now learned how to:
- Solve quadratic inequalities
- Use inequality notation and represent solutions on a number line
- List integers that are in the solution set
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.