GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
Adding and subtracting fractions Multiplying and dividing fractions Substitution Rearranging equations Changing the subject of a formula SOHCAHTOA Pythagoras theoremThis topic is relevant for:

Trig Identities
Here we will learn about trigonometric identities, including recognising and working with key trigonometric identities.
There are also trigonometry worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are trigonometric identities?
Trigonometric identities show relationships between trigonometric functions. These are not examined in GCSE Mathematics but are covered in Level 2 Further Mathematics, Additional Mathematics and IGCSE Further Mathematics courses.
An identity is an equation that is always true.
For example, when we expand the bracket 2(x+1) we get 2x+2. These two functions of x are identical and so we use the identity symbol (a triple equals symbol) to show that 2(x+1) \equiv 2x+2.
We can do the same with the trigonometric ratios of sine, cosine, and tangent.
- \sin(\theta)=\frac{O}{H}
- \cos(\theta)=\frac{A}{H}
- \tan(\theta)=\frac{O}{A}
Where O = Opposite, A = Adjacent, and H = Hypotenuse for the right-angled triangle with angle \theta (theta).
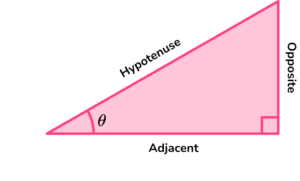
Step-by-step guide: SOHCAHTOA
There are two trigonometric identities that we will look at. These are,
\tan(\theta)\equiv\frac{\sin(\theta)}{\cos(\theta)} \ and \ \sin^2(\theta)+\cos^2(\theta)\equiv1.
Here \sin^2(\theta) is another way of writing (\sin(\theta))^2 .
These two identities will help us prove further identities, using the trigonometric ratios when necessary.
What are trigonometric identities?

How to prove trigonometric identities
In order to prove trigonometric identities:
- Substitute values using the trigonometric ratios or another trigonometric identity.
- Simplify one side of the identity only.
Explain how to prove trigonometric identities

Exact trig values worksheet (includes trig identities)

Get your free trigonometric identities worksheet of 20+ exact trig values questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Exact trig values worksheet (includes trig identities)

Get your free trigonometric identities worksheet of 20+ exact trig values questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREETrigonometric identities examples
Example 1: the relationship between sin, cos and tan
Prove that \ \frac{\sin(\theta)}{\cos(\theta)} \equiv \tan(\theta).
- Substitute values using the trigonometric ratios or another trigonometric identity.
We need to show that \tan (\theta) is the same as \sin (\theta) \div \cos (\theta). To do this we can use the trigonometric ratios.
We know that \ \sin(\theta)=\frac{O}{H}, \ \cos(\theta)=\frac{A}{H}, \ and \ \tan(\theta)=\frac{O}{A}.
As we need to divide \sin(\theta) by \cos(\theta) , this is the same as dividing \frac{O}{H} by \frac{A}{H}.
So we have,
\sin(\theta) \div \cos(\theta) = \frac{O}{H} \div \frac{A}{H}.2Simplify one side of the identity only.
Simplifying the right hand side, we have
\begin{aligned} &\frac{O}{H}\div\frac{A}{H} \\\\ = & \, \frac{O}{H}\times\frac{H}{A} \\\\ =& \, \frac{OH}{AH} \\\\ =& \, \frac{O}{A} \\\\ =& \, \tan(\theta) \end{aligned}Therefore \ \frac{\sin(\theta)}{\cos(\theta)} \equiv \tan(\theta).
Example 2: using Pythagoras’ theorem to prove a trigonometric identity
Prove that \ \sin^2(\theta)+\cos^2(\theta)\equiv1.
Substitute values using the trigonometric ratios or another trigonometric identity.
We need to show that \sin^2(\theta)+\cos^2(\theta) has a value of 1. To do this we can use the trigonometric ratios.
We know that \sin(\theta)=\frac{O}{H} and \cos(\theta)=\frac{A}{H}.
As \sin(\theta)=\frac{O}{H}, multiplying both sides by H to make O the subject, we have O=H\sin(\theta).
As \cos(\theta)=\frac{A}{H}, multiplying both sides by H to make A the subject, we have A=H\cos(\theta).
We now have the length of the opposite side O=H\sin(\theta), and the width of the adjacent side A=H\cos(\theta).
Labelling a triangle using these values, we have,

Pythagoras’ theorem states that a^{2}+b^{2}=c^{2} where a is the height, b is the base, and c is always the hypotenuse.
As the base is H\cos(\theta), the height is H\sin(\theta), and the hypotenuse is H, we can substitute these into Pythagoras’ theorem to get
(H\sin(\theta))^{2}+(H\cos(\theta))^{2}=H^{2}.
Simplify one side of the identity only.
We can only simplify the left hand side and so by squaring both brackets, we have
\begin{aligned} &(H\sin(\theta))^{2}+(H\cos(\theta))^{2}\\\\ =&H^{2}\sin^{2}(\theta)+H^{2}\cos^{2}(\theta)\\\\ =&H^{2}(\sin^{2}(\theta)+\cos^{2}(\theta)) \end{aligned}
This means that as H^{2}(\sin^{2}(\theta)+\cos^{2}(\theta))=H^{2}, so \ \sin^{2}(\theta)+\cos^{2}(\theta)=1 as H^{2}\times{1}=H^{2}.
This proves the identity \sin^{2}(\theta)+\cos^{2}(\theta)\equiv1.
Example 3: proving identities using trig ratios
Prove that \sin(\theta)\div\tan(\theta)\equiv\cos(\theta).
Substitute values using the trigonometric ratios or another trigonometric identity.
We need to show that \sin(\theta)\div\tan(\theta) is the same as \cos(\theta).
We know that \ \sin(\theta)=\frac{O}{H}, \ \tan(\theta)=\frac{O}{A}, \ and \ \cos(\theta)=\frac{A}{H}.
This means that \sin(\theta)\div\tan(\theta) is equivalent to
\frac{O}{H}\div\frac{O}{A}.
Simplify one side of the identity only.
Converting this to one fraction, we have
\begin{aligned} &\frac{O}{H}\div\frac{O}{A}\\\\ =&\frac{O}{H}\times\frac{A}{O}\\\\ =&\frac{OA}{HO}\\\\ =&\frac{A}{H}\\\\ =&\cos(\theta) \end{aligned}
This proves that \sin(\theta)\div\tan(\theta)\equiv\cos(\theta).
Example 4: proving identities using exact trig values
Prove that \cos(60)=1-\sin(30) using the right-angled triangle below.
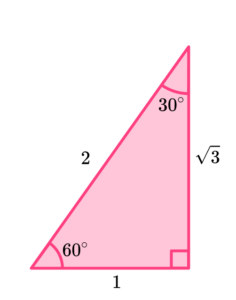
Substitute values using the trigonometric ratios or another trigonometric identity.
We need to show that \cos(60) gives us the same value as 1-\sin(30) using the triangle above.
Using the triangle, we can determine the exact trig value for \cos(60)=\frac{A}{H}=\frac{1}{2}.
We can also determine the exact trig value for \sin(30)=\frac{O}{H}=\frac{1}{2}.
Simplify one side of the identity only.
Calculating 1-\sin(30) we have
1-\sin(30)=1-\frac{1}{2}=\frac{1}{2}.
As \cos(60) is the same as 1-\sin(30), we have proved that \cos(60)=1-\sin(30).
Example 5: proving identities featuring all three trig ratios
Prove that \cos(\theta)\times\tan(\theta)\times\sin(\theta)\equiv\sin^{2}(\theta).
Substitute values using the trigonometric ratios or another trigonometric identity.
We need to show that \cos(\theta)\times\tan(\theta)\times\sin(\theta) is the same as \sin^{2}(\theta).
We can substitute \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)} into the identity to get
\cos(\theta)\times\tan(\theta)\times\sin(\theta)=\cos(\theta)\times\frac{\sin(\theta)}{\cos(\theta)}\times\sin(\theta).
Simplify one side of the identity only.
Simplifying this, we have
\begin{aligned}
& \cos(\theta)\times\frac{\sin(\theta)}{\cos(\theta)}\times\sin(\theta)\\\\
=& \; \frac{\cos(\theta)\times\sin(\theta)\times\sin(\theta)}{\cos(\theta)}\\\\
=& \; \frac{\cos(\theta)\times\sin^{2}(\theta)}{\cos(\theta)} \\\\
=& \; \sin^{2}(\theta)
\end{aligned}
Example 6: using the trigonometric identity sin2(θ) + cos2(θ) = 1
Prove that 6(3\sin^{2}(\theta))+2(9\cos^{2}(\theta))=18.
Substitute values using the trigonometric ratios or another trigonometric identity.
We need to show that 6(3\sin^{2}(\theta))+2(9\cos^{2}(\theta)) can be simplified to make 18.
As there are no substitutions necessary, we can move on to step 2.
Simplify one side of the identity only.
Expanding both brackets gives us
18\sin^{2}(\theta)+18\cos^{2}(\theta).
Removing a common factor of 18, we get
18(\sin^{2}(\theta)+\cos^{2}(\theta)).
As \sin^{2}(\theta)+\cos^{2}(\theta)=1, \ 18\times{1}=18.
We have therefore proven that 6(3\sin^{2}(\theta))+2(9\cos^{2}(\theta))=18.
Common misconceptions
- Treating an identity as an equation that needs balancing
An identity cannot be balanced. It is a statement that two expressions or functions are mathematically identical. For example, 3x+6\equiv{3}(x+2) as when we factorise 3(x+6) we get the expression 3(x+2).
- Mixing up SOHCAHTOA
It is key to remember the three trig ratios that are written as the mnemonic SOHCAHTOA. This way you will not confuse the relationships between the sides and the angles.
Practice trigonometric identities questions
1. Which of the following trigonometric identities is mathematically correct?




As \sin(\theta)=\frac{O}{H} and \cos(\theta)=\frac{A}{H},
\sin(\theta)\div\cos(\theta)=\frac{O}{H}\div\frac{A}{H}=\frac{O}{H}\times\frac{H}{A}=\frac{OH}{HA}=\frac{O}{A}=\tan(\theta).
2. Which of the following trigonometric identities is mathematically correct?




As \sin(\theta)=\frac{O}{H}, multiplying both sides by H to make O the subject,
we have O=H\sin(\theta).
As \cos(\theta)=\frac{A}{H}, multiplying both sides by H to make A the subject,
we have A=H\cos(\theta).
As the base is H\cos(\theta), the height is H\sin(\theta), and the hypotenuse is H, we can substitute these into Pythagoras’ theorem to get,
(H\sin(\theta))^{2}+(H\cos(\theta))^{2}=H^{2}
\begin{aligned} &(H\sin(\theta))^{2}+(H\cos(\theta))^{2}\\\\ =&H^{2}\sin^{2}(\theta)+H^{2}\cos^{2}(\theta)\\\\ =&H^{2}(\sin^{2}(\theta)+\cos^{2}(\theta)) \end{aligned}
This means that as H^{2}(\sin^{2}(\theta)+\cos^{2}(\theta))=H^{2}, \ \sin^{2}(\theta)+\cos^{2}(\theta)=1 as H^{2}\times{1}=H^{2}.
3. Which of the following trigonometric functions is identical to \frac{\tan(\theta)}{\sin(\theta)}?




As \sin(\theta)=\frac{O}{H}, \ \tan(\theta)=\frac{O}{A}, and \cos(\theta)=\frac{A}{H},
\tan(\theta)\div\sin(\theta) is equivalent to
\begin{aligned} &\frac{O}{A}\div\frac{O}{H}\\\\ =\; & \frac{O}{A}\times\frac{H}{O}\\\\ =\; & \frac{OH}{AO}\\\\ =\; & \frac{H}{A}\\\\ =\; & \frac{1}{\cos(\theta)} \end{aligned}
4. Which solution is identical to 2\cos(45)\times\sin(45)?
Use the triangle below to help you.
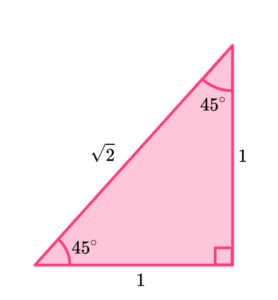




5. Which solution is identical to \cos(\theta)\times\tan(\theta)\div\sin(\theta)?




6. Which solution is identical to \frac{\sin(\theta)}{\sqrt{1-\sin^{2}(\theta)}}?




Trigonometric identities questions
1. Prove that \frac{\sqrt{1-\cos^{2}(\theta)}}{\cos(\theta)}\equiv \tan(\theta).
(2 marks)
(1)
\frac{\sin(\theta)}{\cos(\theta)}= \tan(\theta)(1)
2. (a) Expand and simplify (\sin x + \cos x)^{2}.
(b) Use your solution to part a) to prove that (\sin x + \cos x)^{2} + (\sin x – \cos x)^{2} \equiv 2.
(6 marks)
(a)
(\sin x + \cos x) (\sin x + \cos x) =
(1)
\sin^{2} x + 2 \cos x \sin x + \cos^{2} x(1)
(b)
(\sin x-\cos x)^{2} = \sin^{2} x-2\cos x \sin x + cos^{2} x
(1)
\sin^{2}x+2\cos x \sin x+ \cos^{2}x+ \sin^{2} x-2 \cos x \sin x+\cos^{2}x=2\sin^{2}x+2\cos^{2}x(1)
2\sin^{2}x+2 \cos^{2}x =2(\sin^{2}x+\cos^{2}x)(1)
2\sin^{2}x+2 \cos^{2}x =2(1) =2(1)
3. The axes below show a circle where the point P(H \cos x, \ H \sin x) is a point on the circumference of the circle.
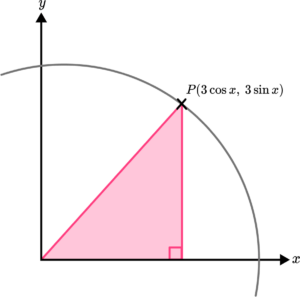
Prove that the radius of the circle is 3.
(4 marks)
(1)
9 \cos^{2} x + 9 \sin^{2} x =r^{2}(1)
9 (\cos^{2} x + \sin^{2} x) = 9(1)
r=\sqrt{9}=3(1)
Learning checklist
You have now learned how to:
- Use Pythagoras’ theorem, a^2+b^2=c^2 to prove the trigonometric ratios \sin(\theta)=\frac{O}{H}, \ \cos(\theta)=\frac{A}{H} and \tan(\theta)=\frac{O}{A}
- Use the trigonometric ratios to prove trigonometric identities
- Extend and formalise your knowledge of ratio and proportion, including trigonometric ratios
The next lessons are
More trigonometric functions and identities
Other trig functions that are studied in a level Mathematics include
- Secant (sec \theta)
- Cosecant (csc \theta)
- Cotangent (cot \theta)
We also study trigonometric values beyond 90 degrees (outside of the limits of a right-angled triangle). These include double-angle formulas (double-angle identities), and conversely half-angle formulas (half-angle identities). These allow us to form trigonometric equations.
At A-level, we use a different measurement for an angle called radians where 2\pi radians is a full turn (360^{\circ}), \pi radians is a half turn (180^{\circ}), \frac{\pi}{2} radians is a quarter turn (90^{\circ}), etc.
We also work with the integrals and derivatives of different trigonometric functions to form other trig equations.
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.