GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

Ratio Types of angles Angle rules Coordinates maths

This topic is relevant for:

GCSE Maths Geometry and Measure Congruence And Similarity

Similar Shapes

Similar‌ ‌Shapes‌

Here‌ ‌we‌ ‌will‌ ‌learn‌ ‌about‌ ‌similar‌ ‌shapes‌ ‌in‌ ‌maths,‌ ‌including‌ ‌what‌ ‌they‌ ‌are‌ ‌and‌ ‌how‌ ‌to‌ ‌identify‌ ‌similar‌ ‌shapes.‌ ‌We‌ ‌will‌ ‌also‌ ‌solve‌ ‌problems‌ ‌involving‌ ‌similar‌ ‌shapes‌ ‌where‌ ‌the‌ ‌scale‌ ‌factor‌ ‌is‌ ‌known‌ ‌or‌ ‌can‌ ‌be‌ ‌found.‌

There‌ ‌are‌ ‌similar‌ ‌shapes‌ ‌worksheets‌ ‌based‌ ‌on‌ ‌Edexcel,‌ ‌AQA‌ ‌and‌ ‌OCR‌ ‌exam‌ ‌questions,‌ ‌along‌ ‌with‌ ‌further‌ ‌guidance‌ ‌on‌ ‌where‌ ‌to‌ ‌go‌ ‌next‌ ‌if‌ ‌you’re‌ ‌still‌ ‌stuck.‌

What are similar shapes?

Similar shapes are enlargements of each other using a scale factor.

All the corresponding angles in the similar shapes are equal and the corresponding lengths are in the same ratio.

E.g.

These two rectangles are similar shapes.

The scale factor of enlargement from shape A to shape B is $2$ .

The angles are all $90^o$

The ratio of the bases is $2:4$ which simplifies to $1:2$

The ratio of the heights is also $1:2$

E.g.

These two parallelograms are similar shapes.

The scale factor of enlargement from shape A to shape B is $3.$

The corresponding angles are all equal, $45^o$ and $135^o$ .

The ratio of the bases are $3:9$ which simplifies to $1:3$

The ratio of the perpendicular heights is also $1:3$

See also: Enlargement

What are similar shapes?

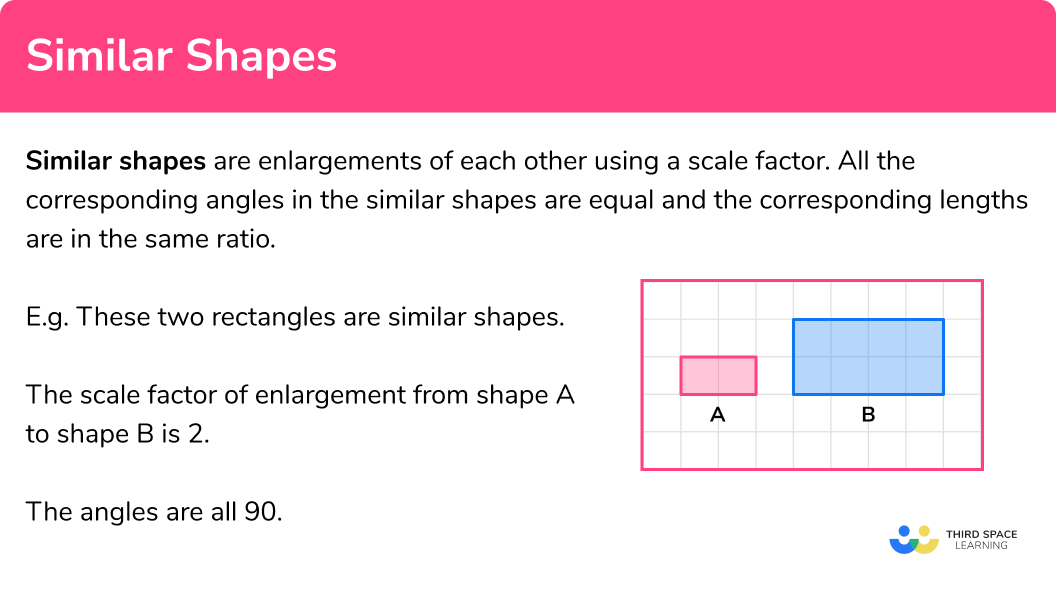
Scale factor for length, area and volume

The scale factors for length, area and volume are not the same.

In Higher GCSE Maths similar shapes are extended to look at area scale factor and volume scale factors

To work out the length scale factor we divide the length of the enlarged shape by the length of the original shape.

To work the area scale factor we square the length scale factor.

To work the volume scale factor we cube the length scale factor.

E.g.

Comparing length A and length B we can work out the scale factor to be $3$ .

Comparing area A and area B we can work out the scale factor to be $9$ .
This is the same as $3^2$ .

Comparing volume A and volume B we can work out the scale factor to be $27$ .
This is the same as $3^3$ .

\begin{aligned} &\text{A} \quad \quad \quad \text{B} \quad \quad \text{Scale factor} \\ \text{Length} \quad \quad \quad &1 \quad \quad \quad \; 3 \quad \quad \quad \quad 3 \\ \text{Area} \quad \quad \quad &1 \quad \quad \quad \;9 \quad \quad \quad \quad 3^2 \\ \text{Volume} \quad \quad \quad &1 \quad \quad \quad \;27 \quad \quad \quad \;\, 3^3 \end{aligned}

Step-by-step guide: Scale factor

Scale factor for length, area and volume

How to decide if shapes are similar

In order to decide if shapes are similar:

Decide which sides are pairs of corresponding sides.
Find the ratios of the sides.
Check if the ratios are the same.

Explain how to decide if shapes are similar

Similar shapes worksheet

Get your free similar shapes worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Similar shapes worksheet

Get your free similar shapes worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on congruence and similarity

Similar shapes is part of our series of lessons to support revision on congruence and similarity. You may find it helpful to start with the main congruence and similarity lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Similar shapes examples

Example 1: decide if shapes are similar

Are these shapes similar?

Decide which sides are pairs of corresponding sides.

The bases of the rectangles are a pair of corresponding sides.

The heights of the rectangles are a pair of corresponding sides.

2Find the ratios of the sides.

When writing the ratios the order is very important.

Here the ratio is length A : length B

The ratio of the bases is $1:2$

The ratio of the heights is $2:4$ which simplifies to $1:2$

3Check if the ratios are the same.

The rectangles are similar shapes. The ratios for the corresponding lengths are the same $1:2.$

The scale factor of enlargement for shape A to shape B is $2$ .

Example 2: decide if shapes are similar

Are these shapes similar?

Decide which sides are pairs of corresponding sides.

The bases of the triangles are a pair of corresponding sides.

The heights of the triangles are a pair of corresponding sides.

Find the ratios of the sides.

When writing the ratios the order is very important.

The ratio of the heights is $5:15$ which simplifies to $1:3$

The ratio of the bases is $7:20$ this can be written as $1: \frac{20}{7}$ or $1:2.857...$

Check if the ratios are the same.

The triangles are NOT similar shapes. The ratios for the corresponding lengths are NOT the same.

How to find a missing length

In order to find a missing side in a pair of similar shapes:

Decide which sides are pairs of corresponding sides.
Find the scale factor.
Use the scale factor to find the missing length.

How to find a missing length

Missing length examples

Example 3: finding a missing length

Here are two similar shapes. Find the length QR.

Decide which sides are pairs of corresponding sides.

Pair up the sides that have measurements. Make sure you pair up the side mentioned in the question.

The sides AB and PQ are a pair of corresponding sides.

The sides BC and QR are a pair of corresponding sides.

Find the scale factor.

The ratio of the lengths AB : PQ is $9:27$ which simplifies to $1:3$

This gives a scale factor of enlargement from rectangle ABCD to rectangle PQRS of $3.$

Use the scale factor to find the missing length.

The ratio of the lengths BC : QR is also $1:3$

We can use the scale factor $3$ as a multiplier to find the missing length.

The missing side has been found. QR $= 12 cm$

Alternatively an equation may be formed and solved:

Example 4: finding a missing length

Here are two similar triangles. Find the length BC.

Decide which sides are pairs of corresponding sides.

Pair up the sides that have measurements. Make sure you pair up the side mentioned in the question. Use the angles to help you.

The sides AB and DE are a pair of corresponding sides.

The sides BC and EF are a pair of corresponding sides.

Find the scale factor.

The ratio of the lengths AB : DE is $12.5 : 25$ which simplifies to $1 : 2$

This gives a scale factor of enlargement from triangle ABC to triangle DEF of $2.$

But we want a scale factor from DEF to ABC which will be $\frac{1}{2}$ .

Use the scale factor to find the missing length.

The ratio of the lengths BC : EF is also $1:2$

We can use the scale factor $\frac{1}{2}$ as a multiplier to find the missing length.

$18\times\frac{1}{2}=9$

The missing side has been found. BC $= 9 \; cm$

Alternatively an equation may be formed and solved:

How to find a missing length in a triangle

In order to find a missing side in a pair of triangles when you are not told that the triangles are similar:

Use angle facts to determine which angles are equal.
Redraw the triangles side by side.
Decide which sides are pairs of corresponding sides.
Find the scale factor.
Use the scale factor to find the missing length.

How to find a missing length in a triangle

Missing length in a triangle examples

Example 5: finding a missing length in a triangle

Work out the value of $x.$

Use angle facts to determine which angles are equal.

Look for equal angles.

angle ACB = angle DCE as vertically opposite angles are equal

There are a pair of parallel sides – AB and DE. This means that there are equal angles as there are alternate angles.

Angle ABC = angle CED (alternate angles)

Angle BAC = angle CDE (alternate angles)

Redraw the triangles side by side.

It makes the problem much easier if you redraw the triangles side-by-side so that it is easier to pair up the corresponding sides.

Decide which sides are pairs of corresponding sides.

Pair up the sides that have measurements. Make sure you pair up the side mentioned in the question. Use the angles to help you.

The sides AC and DC are a pair of corresponding sides.

The sides BC and EC are a pair of corresponding sides.

Find the scale factor.

The ratio of the lengths AC : DC is $4 : 10$ which simplifies to $1 : 2.5$

This gives a scale factor of enlargement from ABC to CDE of $2.5$

Use the scale factor to find the missing length.

The ratio of the lengths BC : EC is also $1 : 2.5$

We can use the scale factor $2.5$ as a multiplier to find the missing length.

$x=5 \times 2.5=12.5$

The value of $x$ has been found, $x=12.5$

Alternatively an equation may be formed and solved:

Example 6: finding a missing length in a triangle

Work out the value of $x.$

Use angle facts to determine which angles are equal.

Look for equal angles.

angle EAB = angle DAC as they are common to both triangles

There are a pair of parallel sides – EB and DC. This means that there are equal angles as there are corresponding angles.

angle AEB = angle ADC (corresponding angles)

angle ABE = angle ACD (corresponding angles)

Redraw the triangles side by side.

It makes the problem much easier if you redraw the triangles side-by-side so that it is easier to pair up the corresponding sides.

Decide which sides are pairs of corresponding sides.

Pair up the sides that have measurements. Make sure you pair up the side mentioned in the question. Use the angles to help you.

The sides AE and AD are a pair of corresponding sides.

The sides EB and DC are a pair of corresponding sides.

Find the scale factor.

The ratio of the lengths AE : AD is $5 : 8$ which simplifies to $1 : \frac{8}{5}$ or $1 : 1.6$

This gives a scale factor of enlargement from ABE to ACD of $1.6$

Use the scale factor to find the missing length.

The ratio of the lengths EB : DC is also $1 : 1.6$

We can use the scale factor $1.6$ as a multiplier to find the missing length.

$x=7 \times 1.6=11.2$

The value of $x$ has been found, $x=11.2$

Alternatively an equation may be formed and solved:

How to find an area or volume using similar shapes

In order to find an area or volume using similar shapes:

Find the scale factor.
Use the scale factor to find the missing value.

How to find an area or volume using similar shapes

Area or volume using similar shapes examples

Example 7: finding an area or volume

These two figures are similar.

The area of shape A is $60 \; cm^2$ .

Find the area of shape B:

Find the scale factor.

Use the given information to write a ratio and work out the scale factor.

When writing the ratios the order is very important.

$\begin{aligned} \text{The ratio of the lengths is} \ \text{length} \; A&: \text{length} \; B\\\\ 5&:10\\\\ \text{which simplifies to} \quad 1&:2 \end{aligned}$

The scale factor of enlargement from shape A to shape B is $2$

Use the scale factor to find the missing value.

As we are finding an area we need to square the ratio of the lengths, and square the scale factor.

$\begin{aligned} \text{The ratio of the lengths is -} \ \text{length} \ A&:\text{length} B\\\\ 1&:2\\\\ \text{The ratio of the areas is -} \ \text{area} \ A&:\text{area} \ B\\\\ 1^2&:2^2\\\\ \text{which simplifies to -}\ \ \ \ \ \ 1&:4 \end{aligned}$

We can use the area scale factor $2^2$ or $4$ as a multiplier to find the missing area.

$60\times 4=240$

The area of shape B is $240 \; cm^2$

Alternatively you can form an equation to solve:

Example 8: finding an area or volume

These two shapes are similar.

The volume of shape A is $400 \; cm^3$ .

Find the volume of shape B:

Find the scale factor.

Use the given information to write a ratio and work out the scale factor.

When writing the ratios the order is very important.

$\begin{aligned} \text{The ratio of the lengths is} \ \text{length } A&: \text{length } B\\\\ 10&:15\\\\ \text{which simplifies to} \quad 1&:1.5 \end{aligned}$

The scale factor of enlargement from shape A to shape B is $1.5$

Use the scale factor to find the missing value.

As we are finding a volume we need to cube the ratio of the lengths, and cube the scale factor.

$\begin{aligned} \text{The ratio of the lengths is -} \ \text{length} \ A&:\text{length} B\\\\ 1&:1.5\\\\ \text{The ratio of the volumes is -} \ \text{volume} \ A&:\text{volume} \ B\\\\ 1^3&:1.5^3\\\\ \text{which simplifies to -}\ \ \ \ \ \ 1&:3.375 \end{aligned}$

We can use the volume scale factor $1.5^3$ or $3.375$ as a multiplier to find the missing volume.

$400\times 3.375=1350$

The volume of shape B is $1350 \; cm^3$

Alternatively you can form an equation to solve:

Common misconceptions

Take care with the order of ratios

Make sure that you are consistent with your ratios.

E.g.

In this example, always write the A value first, and then the B value.

$1 : 3$ and $2 : 6.$

The ratios are equal, so these shapes are similar shapes.

Similar Shapes Common Misconceptions Image 1

In most diagrams the diagrams are NOT drawn to scale

Often diagrams for questions involving similar shapes are NOT drawn to scale. So, use the measurements given, rather than measuring for yourself.

Shapes can be similar but in different orientations

The second shape may be in a different orientation to the first shape. The shapes can still be similar.

E.g.

Here shape A and Shape B are similar.

Shape B is an enlargement of shape A by scale factor $2.$

Similar Shapes Common Misconceptions Image 2

Here shape B has been rotated to make the similarity easier to see.

Similar Shapes Common Misconceptions Image 3

Scaling up or down

If you are finding a missing length in the larger shape you can multiply by the scale factor. The scale factor will be a number greater than $1$ .

If you are finding a missing length in the smaller shape you can multiply by the scale factor, but the scale factor will be a number between $0$ and $1.$

Practice similar shapes questions

Yes – sides in ratio $1:4$

No – sides in ratio $1:3$ and $1:4$

No – sides in ratio $1:3$ and $1:2$

Yes – sides in ratio $1:3$

The shapes are similar as the ratio of the corresponding sides are the same.

The ratio of the bases is $\;\; 3:9$
which simplifies to $\quad \quad \;\; 1:3$
the ratio of the heights is $\; 1:3$

Yes – sides in ratio $2:1$

Yes – sides in ratio $3:1$

No – sides in ratio $2:1$ and $1:2$

No – sides in ratio $3:1$ and $2:1$

The shapes are similar as the ratio of the corresponding sides are the same.

The ratio of the short sides is $\;\; 4:2$
which simplifies to $\quad \quad \quad \quad \;2:1$
the ratio of the long sides is $\quad 8:4$
which simplifies to $\quad \quad \quad \quad \;2:1$

x=11

x=10

x=9

x=8

The ratio of the bases is $\;\; 6:12$
which simplifies to $\quad \quad \;\,1:2$

The scale factor of enlargement is $2$

x=5 \times 2 =10

x=11

x=10

x=12

x=12.5

The ratio of the bases is $\;\; 6:9$
which simplifies to $\quad \quad \;\,1:\frac{9}{6}$
or $\quad \quad \quad \quad \quad \quad \quad \quad \;\;1:1.5$

The scale factor of enlargement is $1.5$

x=8 \times 1.5=12

x=11

x=13

x=16

x=9

Use the parallel lines to identify equal angles.

Similar Shapes Practice Question 5 Image 2

Then we can find pairs of corresponding sides.

Similar Shapes Practice Question 5 Image 3

The ratio of the corresponding sides is $\;\; 4:12$
which simplifies to $\quad \quad \quad \quad \quad \quad \quad \;\;\; 1:3$

The scale factor of enlargement is $\; 3$

x=3 \times 3= 9

x=8

x=9

x=10

x=11

Use the parallel lines to identify equal angles.

Similar Shapes Practice Question 6 Image 2

Then we can find pairs of corresponding sides.

Similar Shapes Practice Question 6 Image 3

The ratio of the corresponding sides is $\;\; 9:6$
which simplifies to $\quad \quad \quad \quad \quad \quad \quad \;\;\; 1:\frac{2}{3}$

The scale factor of enlargement is $\; \frac{2}{3}$

x=12 \times \frac{2}{3}= 8

Learning checklist

You have now learned how to:

Compare lengths using ratio notation and/or scale factors

Solve problems with similar shapes using ratio notation and/or scale factors

Solve problem with areas and volumes using ratio notation and/or scale factors (HIGHER)

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.