Translation

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

Teacher-trusted tutoring

In order to access this I need to be confident with:

2D Shapes Polygons Scale factors Coordinates maths Column vector Decimals

This topic is relevant for:

GCSE Maths Geometry and Measure Transformations

Translation

Here we will learn about translation, including how to translate 2D shapes and how to describe translations.

There are also translation worksheets and problem solving questions based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is translation?

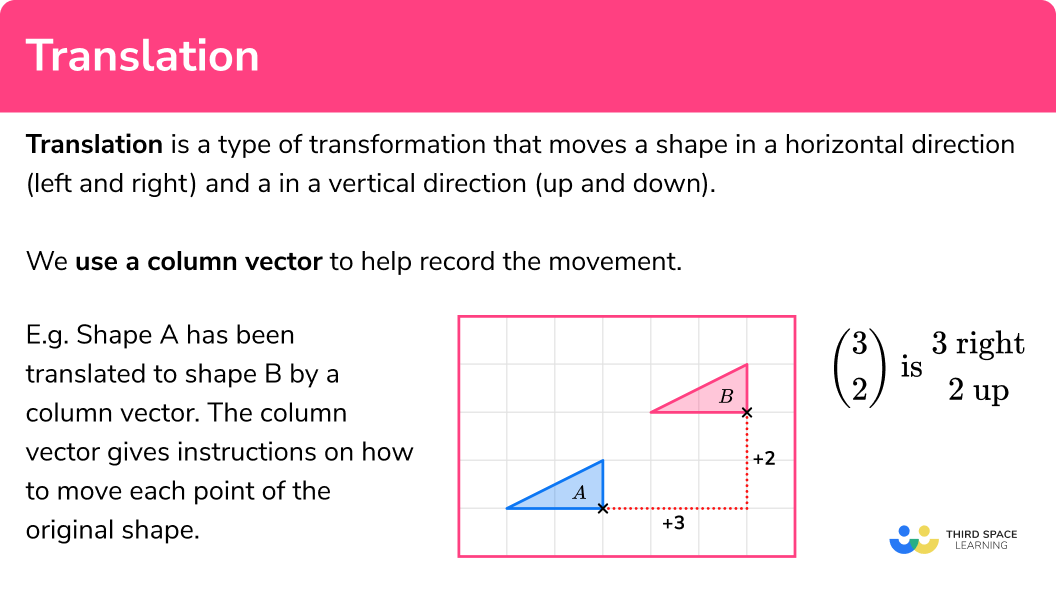
Translation is a type of transformation that moves a shape in a horizontal direction (left and right) and in a vertical direction (up and down).

We use a column vector to help record the movement.

E.g.

Shape A has been translated to shape B by the column vector

\begin{pmatrix} \; 3 \;\\ \; 2 \; \end{pmatrix}

The column vector gives instructions how to move each point of the original shape.

\begin{pmatrix} \; 3 \; \\ \; 2 \; \end{pmatrix} \; \text{is} \; \begin{pmatrix} 3 \ \text{right}\\ 2 \ \text{up}\\ \end{pmatrix}

The inverse transformation would translate shape B back to shape A using the column vector:

\begin{pmatrix} \; -3 \; \\ \; -2 \; \end{pmatrix} \; \text{is} \; \begin{pmatrix} 3 \ \text{left}\\ 2 \ \text{down}\\ \end{pmatrix}

The object is the name of the original shape. The image is the name of the shape after it had been translated. When an object is translated the object and the image have the same orientation. There is no rotation or reflection.

The object and the image are congruent because they are the same shape and the same size.

Using tracing paper can be useful when translating shapes.

Step-by-step guide: Column vector

What is translation?

How to use translation

In order to translate a 2D shape:

Choose a starting point on the shape.
Move it across.
Move it up or down.
Complete the rest of the shape.

How to use translation

Translation maths worksheet

Get your free translation maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Translation maths worksheet

Get your free translation maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Translation maths examples

Example 1: translate a 2D shape

Translate shape A by the column vector $\begin{pmatrix} \; 4 \; \\ \; 1 \; \end{pmatrix}$ and label the image B

Choose a starting point on the shape.

Choose one of the vertices of the shape as the point you are going to move. Let’s use the bottom right hand point of the shape.

2Move it across.

The top number in the column vector is $4$ so move the point $4$ squares to the right.

3Move it up or down.

The bottom number in the column vector is $1$ so move the point $1$ square up.

4Complete the rest of the shape.

You can move each of the other points in the same way and draw in the rest of the 2D shape.

Example 2: translate a 2D shape

Translate shape A by the column vector and label the image B

\begin{pmatrix} \; -1 \;\\ \; 3 \; \end{pmatrix}

Choose a starting point on the shape.

Choose one of the vertices of the shape as the point you are going to move. Let’s use the bottom left hand corner of the shape.

Move it across.

The top number in the column vector is $-1$ so move the point $1$ square to the left.

Move it up or down.

The bottom number in the column vector is $3$ so move the point $3$ squares up.

Complete the rest of the shape.

You can move each of the other points in the same way and draw in the rest of the 2D shape.

Example 3: translate a 2D shape

Translate shape A by the column vector and label the image B

\begin{pmatrix} \; 0 \;\\ \; -4 \; \end{pmatrix}

Choose a starting point on the shape.

Choose one of the vertices of the shape as the point you are going to move. Let’s use the bottom left hand corner of the shape.

Move it across.

The top number in the column vector is $0$ so there is no horizontal movement of the point.

Move it up or down.

The bottom number in the column vector is $-4$ so move the point $4$ squares down.

Complete the rest of the shape.

You can move each of the other points in the same way and draw in the rest of the 2D shape.

How to describe translations

In order to describe a translation of a shape:

Pair up the points.
Work out the horizontal movement.
Work out the vertical movement.
State the column vector.

How to describe translations

Describing translations examples

Example 4: describe a translation

Describe the translation of shape P to shape Q

Pair up the points.

Pair up a point from the object and the corresponding point on the image. Here one pair of points is chosen. It should not matter which pair of points are chosen.

From the object P the point is $(1,1)$

For the image Q the point is $(3,2)$

Work out the horizontal movement.

Using the grid or the $x$ -coordinates, work out the horizontal movement. There is a shift of $2$ to the right.

Work out the vertical movement.

Using the grid or the $y$ -coordinates, work out the vertical movement. There is a shift of $1$ upwards.

State the column vector.

Now we need to write the horizontal shift and the vertical shift in a column vector.

\begin{pmatrix} 2 \ \text{right}\\ 1 \ \text{up}\\ \end{pmatrix} \text{is} \begin{pmatrix} \; 2 \;\\ \; 1 \; \end{pmatrix}

Shape P has been translated to shape Q by the column vector

$\begin{pmatrix} \; 2 \;\\ \; 1 \; \end{pmatrix}$

Example 5: describe a translation

Describe the translation of shape A to shape B

Pair up the points.

Pair up a point from the object and the corresponding point on the image. Here one pair of points is chosen. It should not matter which pair of points are chosen.

From the object A the point is $(4,6)$

For the image B the point is $(1,2)$

Work out the horizontal movement.

Using the grid or the $x$ -coordinates, work out the horizontal movement. There is a shift of $3$ to the left.

Work out the vertical movement.

Using the grid or the $y$ -coordinates, work out the vertical movement. There is a shift of $4$ downwards.

State the column vector.

Now we need to write the horizontal shift and the vertical shift in a column vector.

\begin{pmatrix} 3 \ \text{left}\\ 4 \ \text{down}\\ \end{pmatrix} \text{is} \begin{pmatrix} \; -3 \;\\ \; -4 \; \end{pmatrix}

Shape A has been translated to shape B by the column vector

$\begin{pmatrix} \; -3 \;\\ \; -4 \; \end{pmatrix}$

Example 6: describe a translation

Describe the translation of shape A to shape B

Pair up the points.

Pair up a point from the object and the corresponding point on the image. Here one pair of points is chosen. It should not matter which pair of points are chosen.

From the object A the point is $(1,1)$

For the image B the point is $(1,6)$

Work out the horizontal movement.

Using the grid or the $x$ -coordinates, work out the horizontal movement. There is no horizontal shift.

Work out the vertical movement.

Using the grid or the $y$ -coordinates, work out the vertical movement. There is a shift of $5$ upwards.

State the column vector.

Now we need to write the horizontal shift and the vertical shift in a column vector.

\begin{pmatrix} 0 \ \text{left or right}\\ 5 \ \text{up}\\ \end{pmatrix} \text{is} \begin{pmatrix} \; 0 \;\\ \; 5 \; \end{pmatrix}

Shape A has been translated to shape B by the column vector

$\begin{pmatrix} \; 0 \;\\ \; 5 \; \end{pmatrix}$

Common misconceptions

Check the scale of the coordinate grid

Be careful to consider the scaling on the axes.

What is the column vector for the translation of shape P to shape Q?

Translation Example 6 Common Misconception Image

If we count the squares it may appear that shape P has been translated by the column vector

\begin{pmatrix} \; 6 \;\\ \; 2 \; \end{pmatrix}

But if by considering the scale on the axes, the correct column vector is

\begin{pmatrix} \; 3 \;\\ \; 1 \; \end{pmatrix}

Interpreting the column vector

Remember, the top number is for horizontal movement. A positive number moves the shape to the right and a negative number moves the shape to the left.

The bottom number is for vertical movement. A positive moves the shape upwards and a negative number moves the shape downwards.

Object and image

The original shape is the object and the translated shape is the image. Make sure you know which shape is the original shape and start there when describing transformations such as translations.

Practice translation maths questions

Translation Practice Question 1 Answer 2

Translation Practice Question 1 Answer 3

Translation Practice Question 1 Answer 1

Translation Practice Question 1 Answer 4

Choose a point on the vertex of the shape and move it $3$ to the right and $2$ up.

Do the same with all the points, or carefully draw in the rest of the image.

\begin{pmatrix} \; 3 \;\\ \; 2 \; \end{pmatrix} \text{is} \begin{pmatrix} 3 \ \text{right}\\ 2 \ \text{up}\\ \end{pmatrix}

Translation Practice Question 1 Explanation Image

Translation Practice Question 2 Answer 1

Translation Practice Question 2 Answer 2

Translation Practice Question 2 Answer 3

Translation Practice Question 2 Answer 4

Choose a point on the vertex of the shape and move it $4$ to the left and $1$ up.

Do the same with all the points, or carefully draw in the rest of the image.

\begin{pmatrix} \; -4 \;\\ \; 1 \; \end{pmatrix} \text{is} \begin{pmatrix} 4 \ \text{left}\\ 1 \ \text{up}\\ \end{pmatrix}

Translation Practice Question 2 Explanation Image

Translation Practice Question 3 Answer 2

Translation Practice Question 3 Answer 3

Translation Practice Question 3 Answer 4

Translation Practice Question 3 Answer 1

Choose a point on the vertex of the shape and move it $3$ to the right and $0$ up or down.

Do the same with all the points, or carefully draw in the rest of the image.

\begin{pmatrix} \; 3 \;\\ \; 0 \; \end{pmatrix} \text{is} \begin{pmatrix} 3 \ \text{right}\\ 0 \ \text{up or down}\\ \end{pmatrix}

Translation Practice Question 3 Explanation Image

Translation by

\begin{pmatrix} \; -3 \;\\ \; -2 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; 2 \;\\ \; 3 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; 3 \;\\ \; 2 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; -2 \;\\ \; -3 \; \end{pmatrix}

Choose a point on the object shape A and its corresponding point on the image shape B. Count the shift in the horizontal direction. Count the shift in the vertical direction.

Translation Practice Question 4 Explanation Image

\begin{pmatrix} 2 \ \text{right}\\ 3 \ \text{up}\\ \end{pmatrix} \text{is} \begin{pmatrix} \; 2 \;\\ \; 3 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; 4 \;\\ \; 3 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; -3 \;\\ \; 4 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; 4 \;\\ \; -3 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; -3 \;\\ \; -4 \; \end{pmatrix}

Choose a point on the object shape A and its corresponding point on the image shape B. Count the shift in the horizontal direction. Count the shift in the vertical direction.

Translation Practice Question 5 Explanation Image

\begin{pmatrix} 4 \ \text{right}\\ 3 \ \text{up}\\ \end{pmatrix} \text{is} \begin{pmatrix} \; 4 \;\\ \; -3 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; 1 \;\\ \; -4 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; 4 \;\\ \; -1 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; 1 \;\\ \; 4 \; \end{pmatrix}

Translation by

\begin{pmatrix} \; 4 \;\\ \; 1 \; \end{pmatrix}

Choose a point on the object shape P and its corresponding point on the image shape Q. Count the shift in the horizontal direction. Count the shift in the vertical direction.

\begin{pmatrix} 1 \ \text{right}\\ 4 \ \text{down}\\ \end{pmatrix} \text{is} \begin{pmatrix} \; 1 \;\\ \; -4 \; \end{pmatrix}

Translation Practice Question 6 Explanation Image.1

Translation maths GCSE questions

1. A shape is translated by the vector

\begin{pmatrix} \; 0 \;\\ \; -3 \; \end{pmatrix}

In which direction does the shape move?

Circle your answer.

Up Down Left Right

(1 mark)

Show answer

Down

(1)

2. Translate trapezium P by the vector

\begin{pmatrix} \; 1 \;\\ \; -3 \; \end{pmatrix}

Translation GCSE Question 2 Image 1

(2 marks)

Show answer

Translation GCSE Question 2 Image 2

For a translation (new shape is same orientation as the original shape)

(1)

For the correct translation

(1)

3. Describe the single transformation that maps Shape A onto shape B.

Translation GCSE Question 3

(2 marks)

Show answer

Translation

(For stating translation)

(1)

\begin{pmatrix} \; 2 \;\\ \; 3 \; \end{pmatrix}

(For the correct vector)

(1)

Learning checklist

You have now learned how to:

Translate a 2D shape by a vector

Describe translations as 2D vectors

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.