High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Types of triangles Perimeter Area Calculator skills Rearranging equations FractionsTrig formulas
Here you will learn about trig formulas, or trigonometry formulas, including the three trigonometric functions; the sine function, the cosine function, and the tangent function,
You will also look at the inverse trigonometric functions, the sine rule, cosine rule, and the trigonometric formula for the area of a triangle.
Students will first learn about trig formulas as part of trigonometric functions in high school.
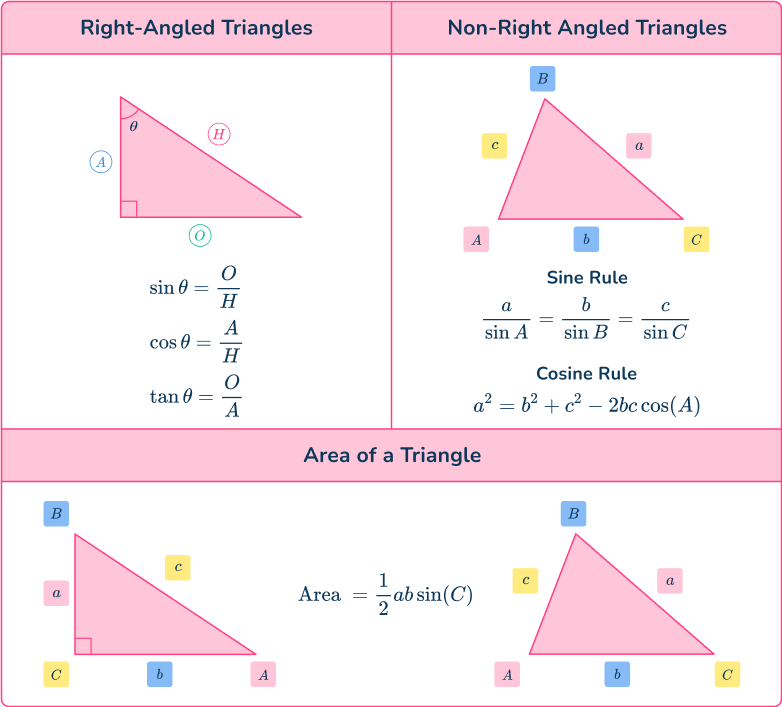
What are trig formulas?
Trig formulas, or trigonometry formulas, are formulas that are used to represent relationships between the parts of a triangle including the side lengths, angles and the area.
To solve problems using trig formulas, you need to be able to use the information provided to deduce which trigonometric formula you need to use.
What are trig formulas?

![[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)
![[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 9 to 12 students’ understanding of Trigonometry. 15+ questions with answers covering a range of 9th to 12th grade trigonometry topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)
![[FREE] Trigonometry Check for Understanding Quiz (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 9 to 12 students’ understanding of Trigonometry. 15+ questions with answers covering a range of 9th to 12th grade trigonometry topics to identify areas of strength and support!
DOWNLOAD FREETrigonometry formulas for right-angled triangles
Basic trigonometry focuses on the right-angled triangle.

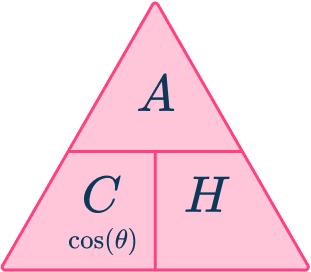
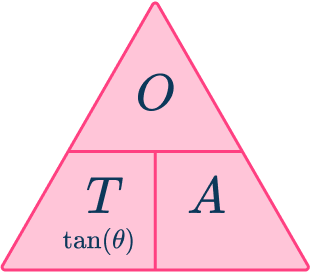
The three trigonometric functions you use are sine cosine and tangent These three functions relate an angle to two sides of a right-angled triangle, giving us the three trigonometric ratios.
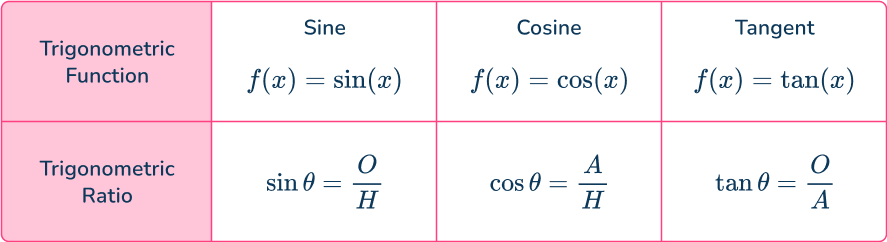
The letter represents a value, hence, is a function of the value
The symbol represents the angle.
The letter represents the opposite side to the angle
The letter represents the adjacent side to the angle
The letter represents the hypotenuse of the right-angled triangle (which is always the side of the triangle facing the right-angle). Also known as the longest side of the triangle.

Step-by-step guide: SOHCAHTOA
Inverse trigonometric functions
When you know two of the three sides of a right angled triangle and you want to find a missing angle, you need to use inverse trigonometric functions. The three inverse trigonometric functions are:
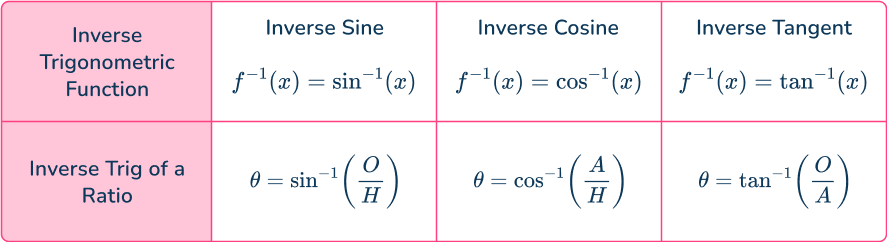

Step-by-step guide: Trig functions
Trigonometric formulas in non-right angled triangles
You can use trigonometry in all types of triangles including scalene, equilateral and isosceles.
Sine rule
The sine rule (sometimes called the law of sines) is the relationship between the sine of an angle, and the side opposite that angle.
More specifically the ratio of the sine of an angle and the opposing side to that angle is the same for all three angles / sides. As a formula, this is written as
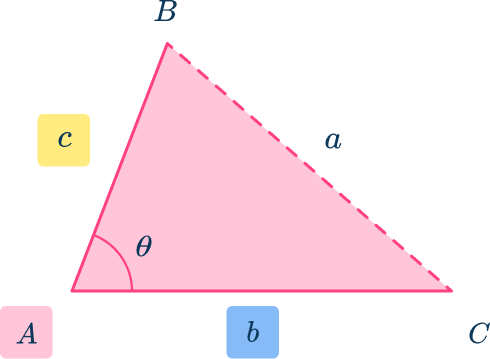
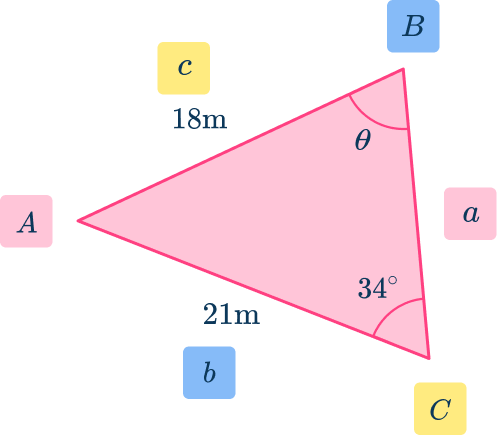
Where and are the three sides of a triangle, and and are the angles that face their opposing side (see the diagram below).
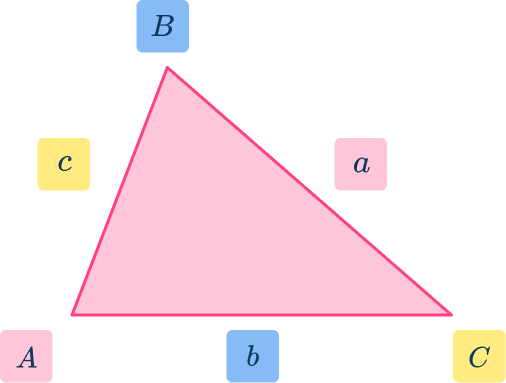
Notice that the upper case letters denote the angles, and the lower case letters denote the side lengths where is opposite is opposite and is opposite
The equation above shows how all three side lengths, divided by the sine of the angle facing that side, are the same value. You only need to work with a pair of letters, giving us the working formula for the law of sines.
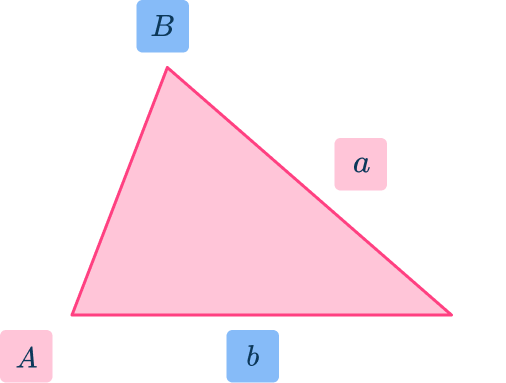
You can use the sine rule to find:
- a missing side using this arrangement of the formula.
By rearranging the formula to make the unknown side the subject, you have
- a missing angle using this arrangement of the formula.
By rearranging the formula to make the unknown angle the subject, you have
Step-by-step guide: Law of sines
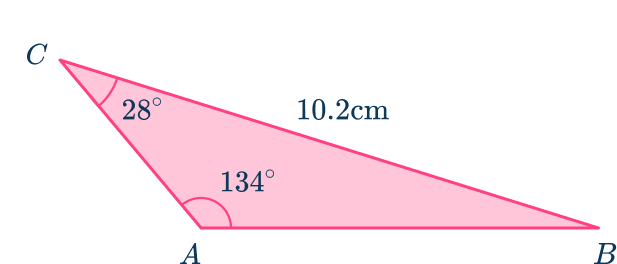
For example,
Below is a non-right angled triangle. You can use the law of sines to find the length
Cosine rule
The cosine rule (sometimes called the law of cosines ) is the relationship between the cosine of an angle, and all three sides of the triangle.
As a formula, this is written as
Where and are the three sides of a triangle, and is the angle between the two sides of and (see the diagram below).
Notice that the upper case is an angle, and the lower case letters are the side lengths where is opposite and and are the two sides that surround the angle
You need to use the cosine rule when you don’t know one of the four values of or
You can use the cosine rule to find
- a missing side by using this arrangement of the formula,
- a missing angle by using this arrangement of the formula,
Step-by-step guide: Law of cosines
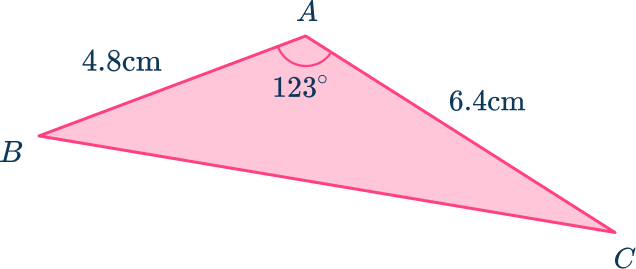
For example,
Below is a non-right angled triangle. You can use the law of cosine to find the length
Area of a triangle
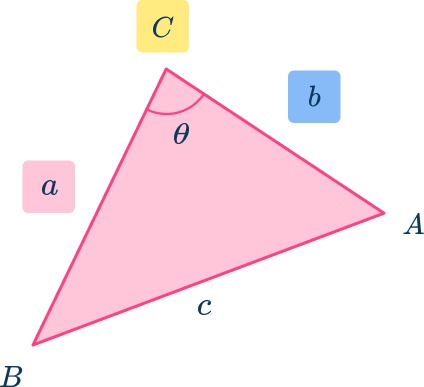
You can calculate the area of any triangle if you need to know two sides and the included angle between those two sides. The formula is
Where is the angle between the two sides of and (see the diagram below).
You can also find a missing angle knowing the area of the triangle and by rearranging the formula to find the angle
You can find a missing side length knowing the area of the triangle and rearranging the formula to find a missing side length
For example,
You can find the area of the triangle below using the trigonometric formula for the area of any triangle.
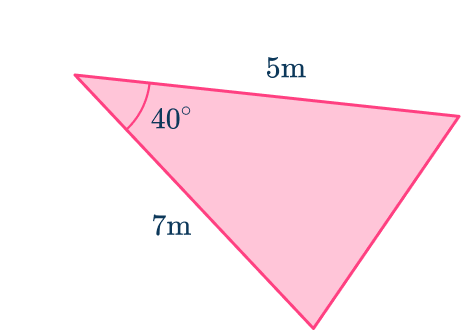
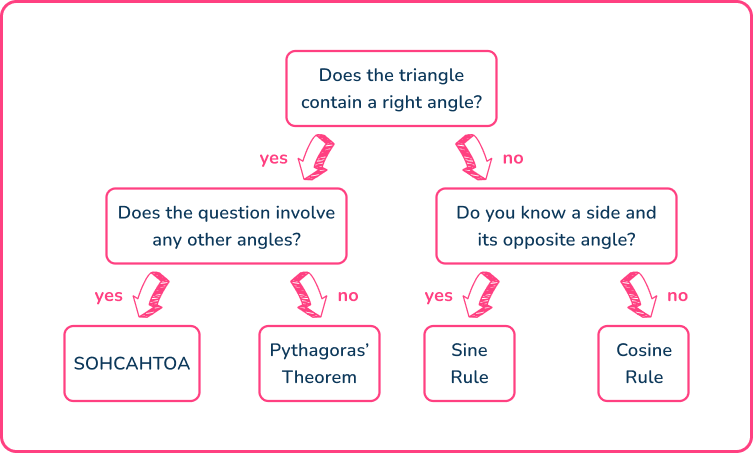
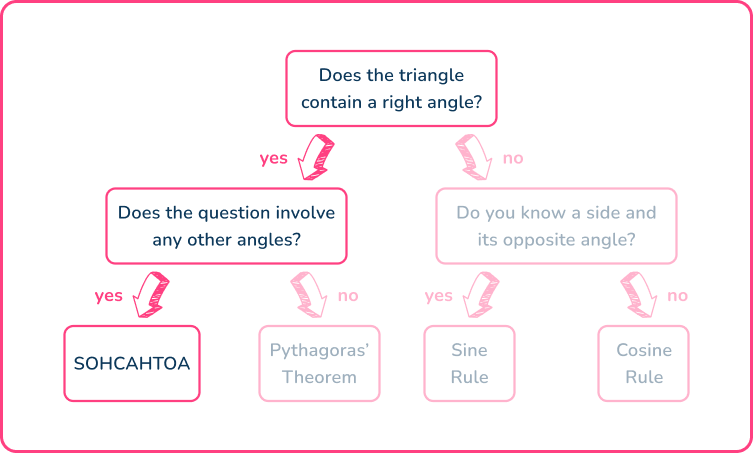
Choosing the correct trigonometric formula
In order to determine which trigonometric formula you need to use, the flow chart below can help you decide.
Remembering that, to find the area of any triangle, you can use the sine rule for area.
Common Core State Standards
How does this relate to high school math?
- High School – Functions – Trigonometric Functions (HSF.TF.A.3)
Use special triangles to determine geometrically the values of sine, cosine, tangent for and and use the unit circle to express the values of sine, cosine, and tangent for and in terms of their values for where is any real number.
How to solve problems using trigonometry formulas
In order to solve problems using trigonometry formulas:
- Determine which trigonometry formula is needed to answer the question.
- Label each side and angle appropriately.
- Substitute known values into the formula.
- Solve for the unknown value.
Trigonometry formulas examples
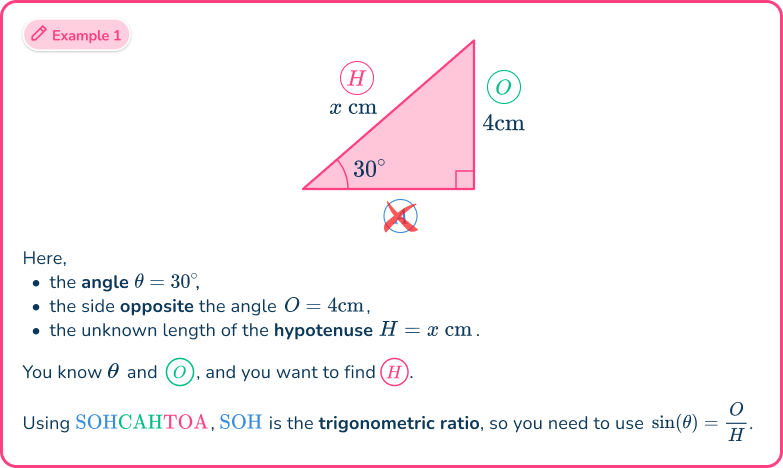
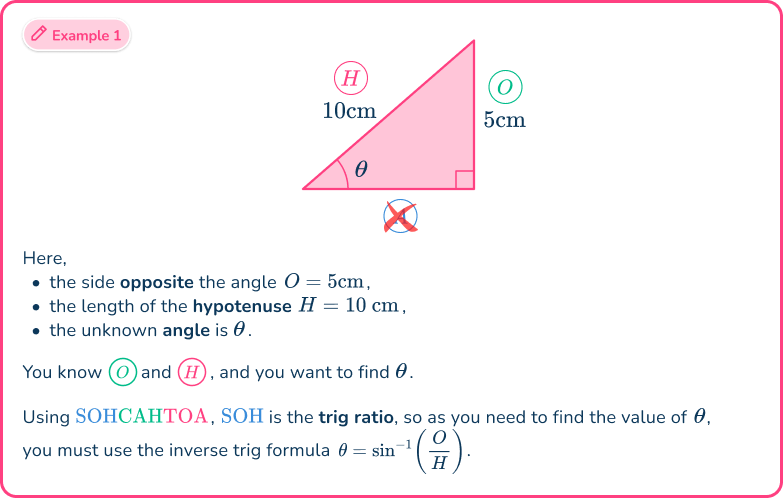
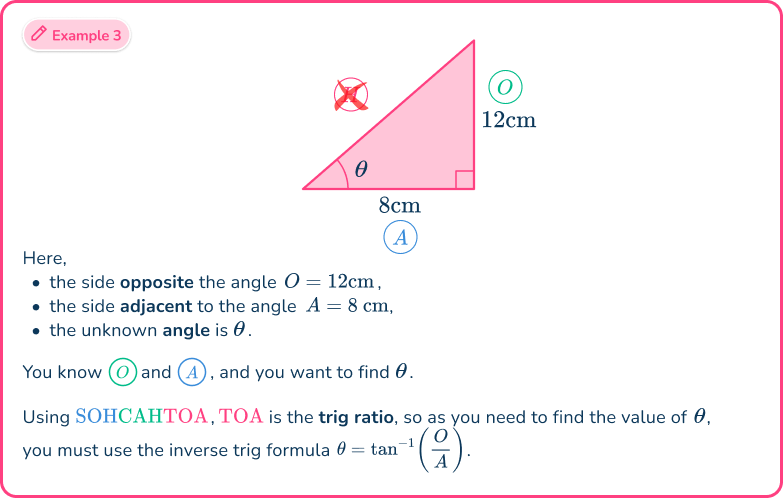
Example 1: SOHCAHTOA (missing side)
Calculate the length of the side labeled Write your answer correctly to the nearest hundredth.
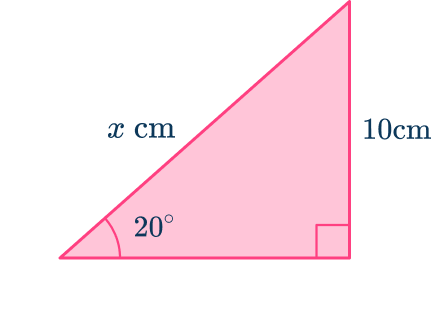
- Determine which trigonometry formula is needed to answer the question.
Using the flowchart,
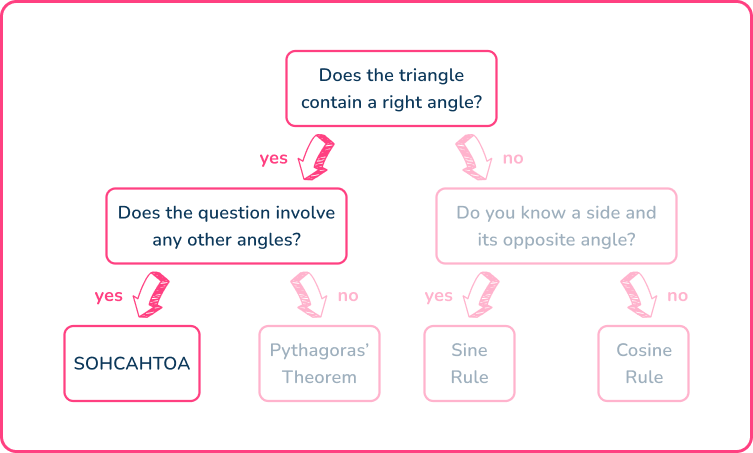
This means that you need to use either of the three trig ratios of sine, cosine or tangent. You can work out which one in the next step.
2Label each side and angle appropriately.
From the angle of
- the side opposite the angle
- the hypotenuse
- the adjacent side has no value and so is not used.
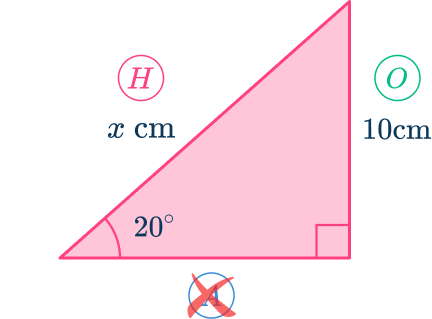
As you know the opposite side and you want to find the hypotenuse, the trigonometric ratio that you have to use is
Here, you used the abbreviation where is the sine ratio of the opposite and the hypotenuse
3Substitute known values into the formula.
As and substituting these values into the formula you have
4Solve for the unknown value.
Multiplying both sides by gives us
Dividing both sides by gives us
This means that the length
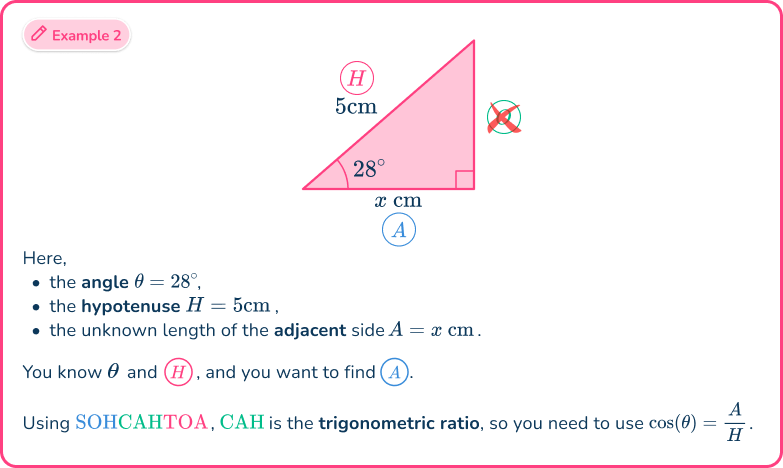
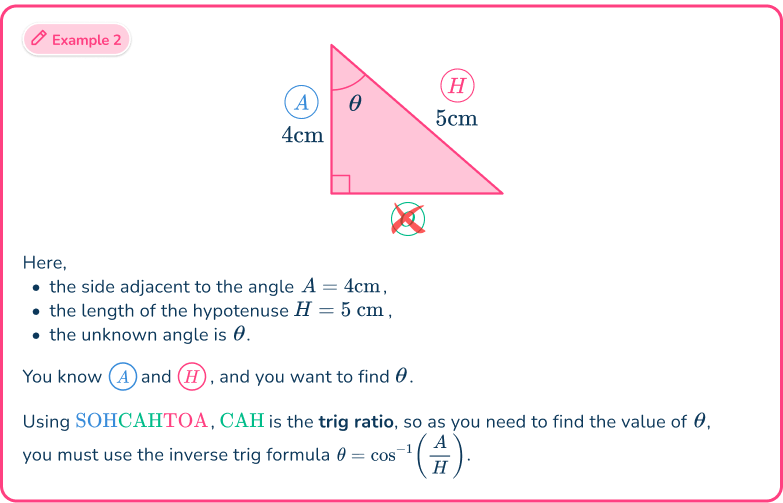
Example 2: SOHCAHTOA (missing angle)
Determine the size of the missing angle, marked in the triangle below. Write your answer correctly to the nearest hundredth.
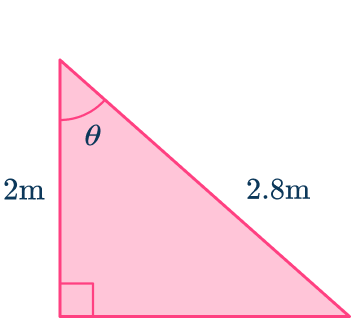
Determine which trigonometry formula is needed to answer the question.
Using the flowchart,
This means that you need to use either of the three trig ratios of sine, cosine or tangent. You can work out which one in the next step.
Label each side and angle appropriately.
From the angle of
- the side adjacent to the angle
- the hypotenuse
- the opposite side has no value and so is not used.
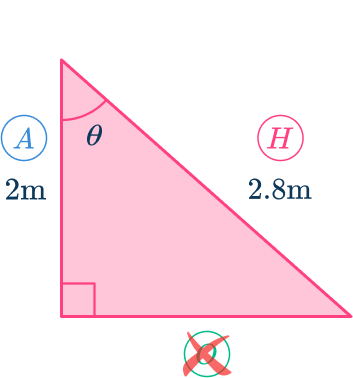
As you know the adjacent side and the hypotenuse, the trigonometric ratio that you have to use is
However, as you need to find the missing angle, you need to use the inverse trigonometric formula
Here, you used the abbreviation where is the cosine ratio of the adjacent and the hypotenuse
Substitute known values into the formula.
As and is unknown, substituting these values into the formula you have
Solve for the unknown value.
This means that the angle
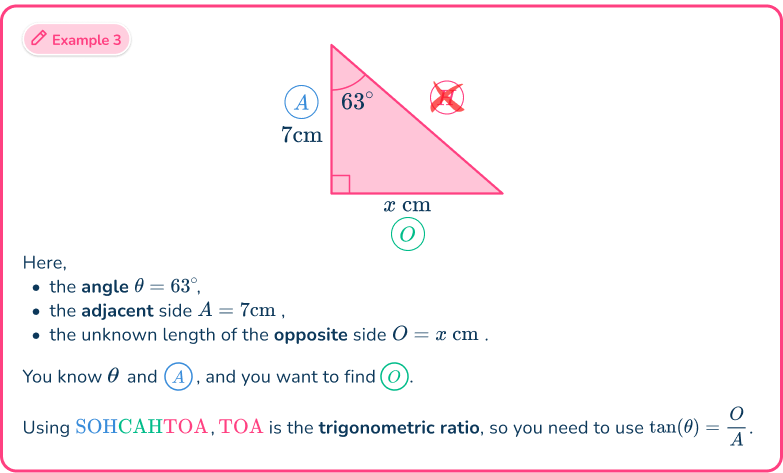
Example 3: SOHCAHTOA
Determine the missing length of the right-angled triangle below. Write your answer to the nearest hundredth.
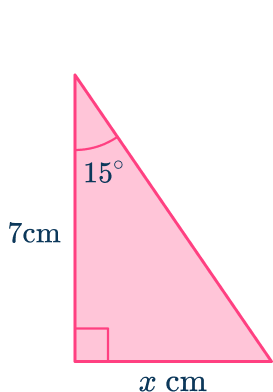
Determine which trigonometry formula is needed to answer the question.
Using the flowchart,
This means that you need to use either of the three trig ratios of sine, cosine or tangent. You can work out which one in the next step.
Label each side and angle appropriately.
From the angle of
- the side adjacent to the angle
- the opposite side to the angle
- the hypotenuse has no value and so is not used.
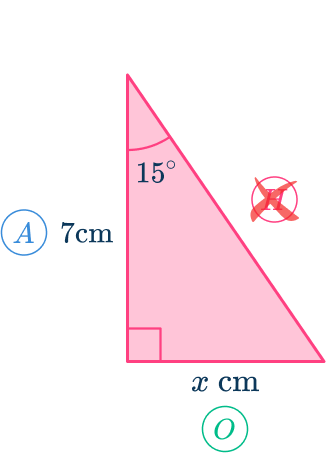
As you know the opposite side and the adjacent side, the trigonometric ratio that you have to use is
Here, you used the abbreviation where is the tangent ratio of the opposite and the adjacent
Substitute known values into the formula.
As and substituting these values into the formula you have
Solve for the unknown value.
Multiplying both sides by gives us
This means that
The length
Example 4: cosine rule
Determine the length of the side labeled for the triangle below. Write your answer correctly to the nearest hundredth.
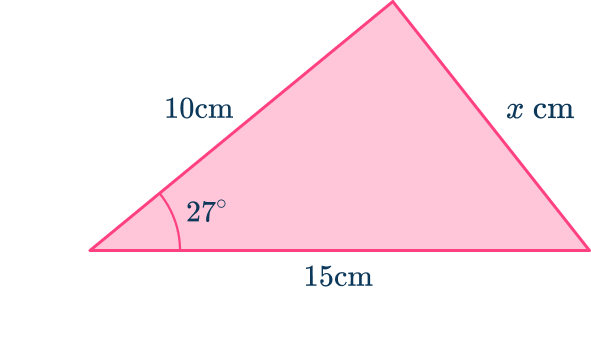
Determine which trigonometry formula is needed to answer the question.
Using the flowchart,
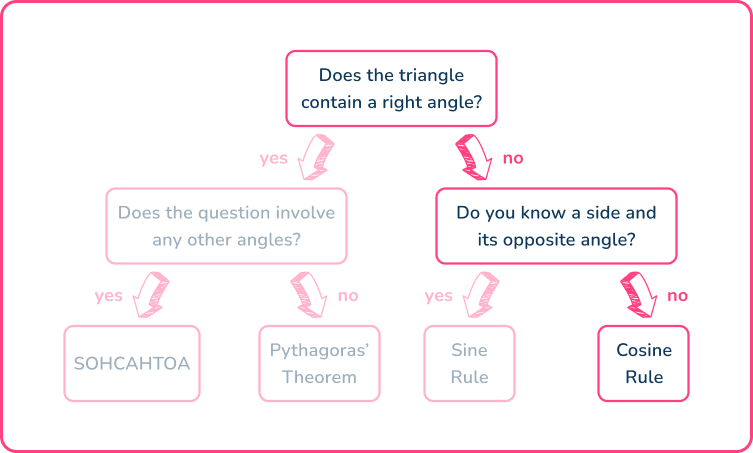
For this question, you can only use the cosine rule (the law of cosines),
Label each side and angle appropriately.
From the angle at of
- the side next to the angle is
- the side next to the angle is
- the side opposite the angle is
- the angles at and have no values and so they are not used.
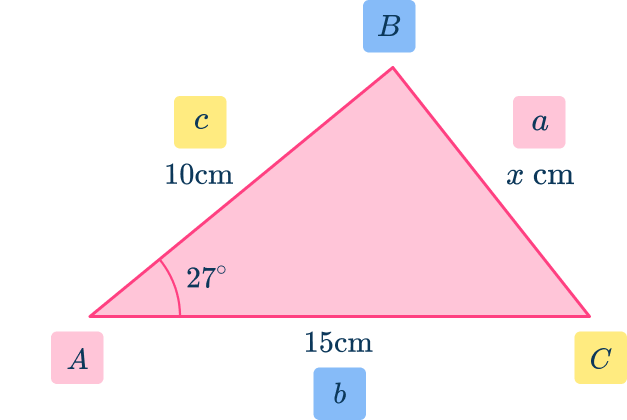
Substitute known values into the formula.
As and substituting these into the cosine rule you have
Solve for the unknown value.
The length
Example 5: sine rule
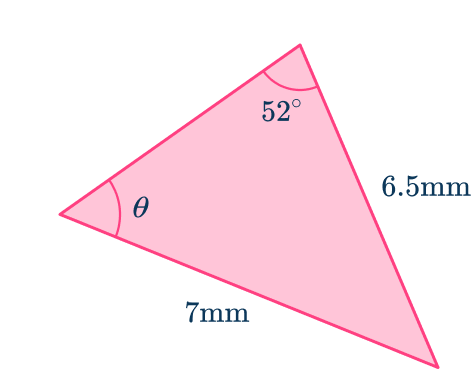
Determine the size of the missing angle Write your answer to the nearest hundredth.
Determine which trigonometry formula is needed to answer the question.
Using the flowchart,
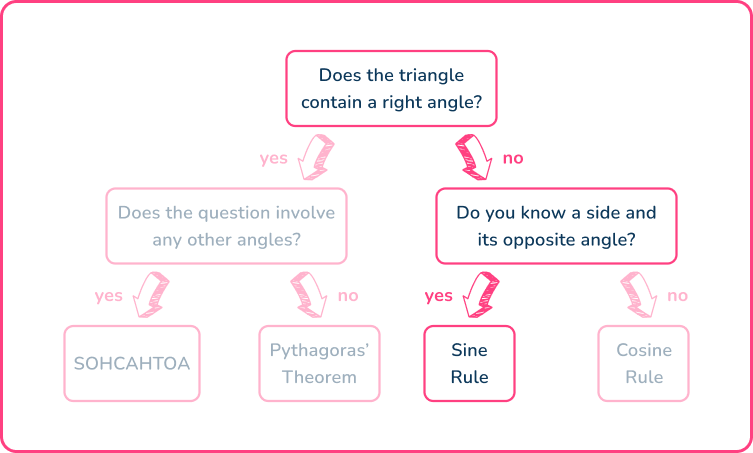
For this question, you can only use the sine rule (the law of sines),
Label each side and angle appropriately.
From the angle at of
- the side opposite the angle is
- the side next to the angle is
- the angle at
- the angle at and the length of side have no values and so they are not used.
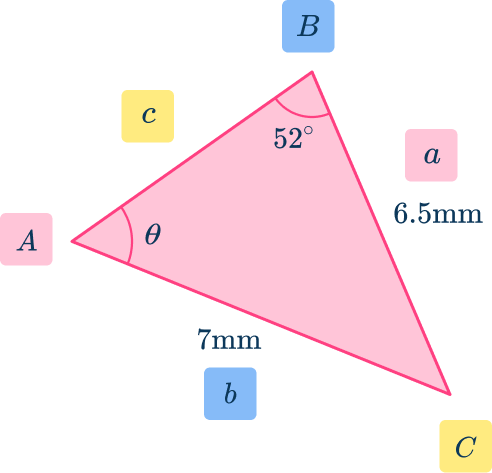
Substitute known values into the formula.
As and substituting these into the sine rule you have
Remember that you do not need to use all three parts of the formula for the sine rule so you only have one equals sign.
Solve for the unknown value.
Multiplying both sides by you have
Multiplying both sides by you have
Dividing both sides by you have
Calculating the inverse sine of each side, you have
This gives the value
Example 6: area using trigonometry formulae
Calculate the area of the triangle below. Write your answer correctly to the nearest hundredth.
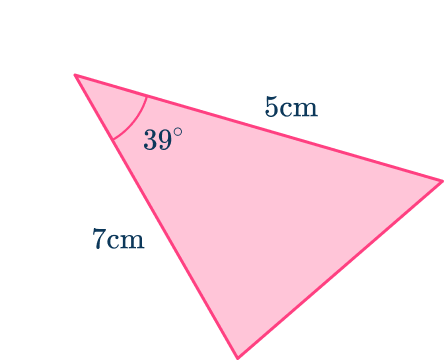
Determine which trigonometry formula is needed to answer the question.
As you are calculating the area of the triangle, you use the sine rule for area
Label each side and angle appropriately.
From the angle at of
- the side next to the angle is
- the side next to the angle is
- the angles at and and the length of side have no values and so they are not used.
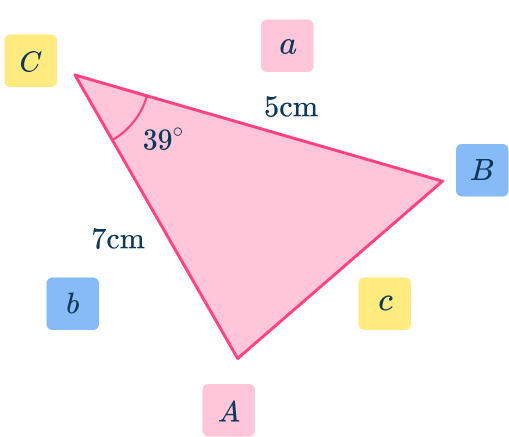
Substitute known values into the formula.
As and substituting these into the formula for the area of a triangle using the sine rule you have
Solve for the unknown value.
As you are finding the area, the units are in
This gives the solution
Teaching tips for trig formulas
- Make sure students understand the fundamental trigonometric ratios (sine, cosine, tangent) and their relationships in right-angled triangles before diving into formulas.
- Use graphing calculators or software to demonstrate how trigonometry functions work. Interactive apps and online graphing tools can make learning more dynamic.
- Show how key formulas like the Pythagorean identity (expressing the Pythagorean theorem in terms of trigonometric functions), angle sum and difference formulas, and double-angle formulas are derived. Understanding these derivations helps students see the connections between the formulas.
- Periodically review trigonometric identities and formulas with quick quizzes, group activities, or games. This helps reinforce the concepts and ensures that students retain the information.
Easy mistakes to make
- Labeling a triangle incorrectly
For example, this triangle has been incorrectly labeled with the side next to the angle rather than opposite it.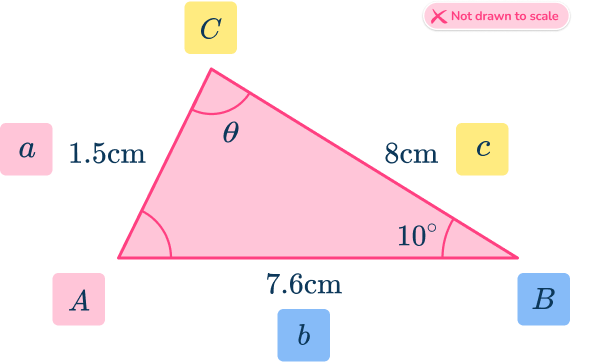
- Using the incorrect trigonometric function
If the triangle is incorrectly labeled, it can lead to the use of the incorrect standard or inverse trigonometric functions and formulae.
- Rounding the decimal too early
Always use as many decimal places as possible throughout the calculation, then round the final solution.
- Using the sine rule instead of the cosine rule
In order to use the sine rule, you need to have pairs of opposite angles and sides.
- Not using the included angle
For the cosine rule and the area of a triangle using the angle is included between the two sides. Using any other angle will result in an incorrect solution.
- Using
If the vertical height of a triangle is not available then you cannot calculate the area by halving the base times the height.
- Using the inverse trig function instead, inducing a mathematical error
If the inverse trig function is used instead of the standard trig function, the calculator may return a math error as the solution does not exist.
- Trigonometry can only be used in right-angled triangles
The use of trigonometry does not have to be limited to a right-angled triangle where all angles are acute angles. You can also use the law of cosines, the law of sines, and the area of a triangle using the sine rule on triangles that are not right-angled.
Related trigonometry lessons
- Trigonometry
- How to find the exact value of a trig function
- Sin cos tan
- Trig formula for area of a triangle
- Trig identities
- Trig table
Practice trigonometry formulas questions
1. Determine the size of the missing side marked in the triangle below. Write your answer to the nearest hundredth.
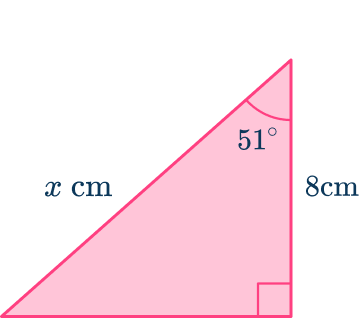




After labeling the triangle with and
2. Determine the size of the missing angle marked in the triangle below. Write your answer to the nearest hundredth.
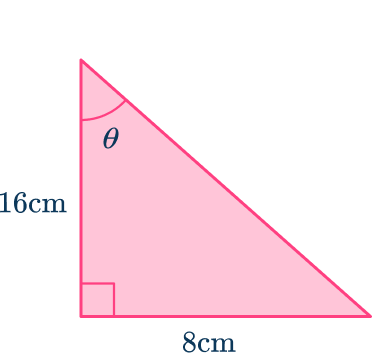




After labeling the triangle with and
SOH CAH TOA
3. Determine the size of the missing angle marked in the triangle below. Write your answer to a suitable degree of accuracy.
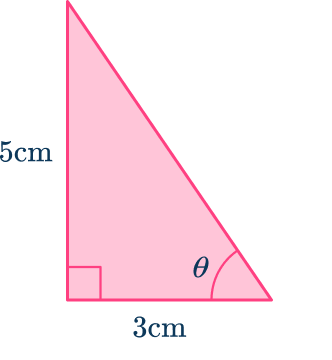




After labeling the triangle with and
SOH CAH TOA
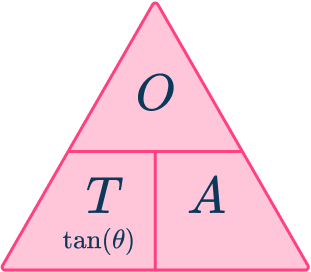
4. Determine the size of the missing length marked in the triangle below. Write your answer to the nearest hundredth.
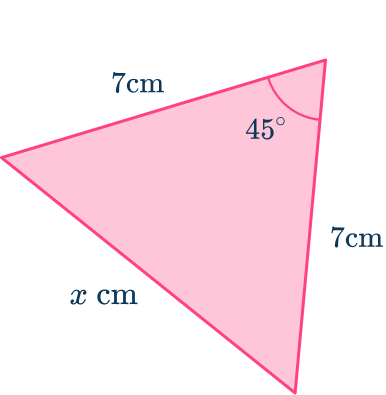




Labeling the sides and angles, you have
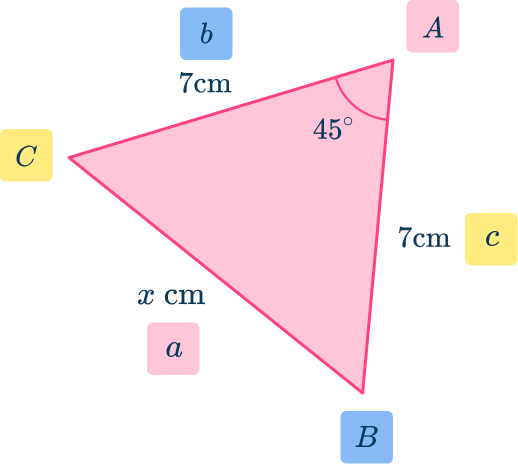
As you know the two side lengths of and and the included angle at you need to use the cosine rule (the law of cosines) to determine the length of side
5. Determine the size of the missing angle marked in the triangle below. Write your answer to the nearest hundredth.
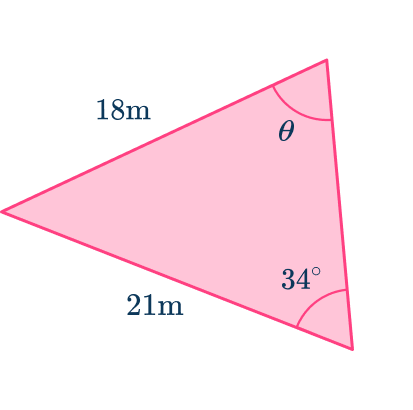




Labeling the sides and angles, you have
As you know the angle at the length of side the length of side and you want to determine the angle at you need to use the sine rule (the law of sines) to determine the length of angle
Being careful with the labeling and the correct version of the sine rule, you have
6. Determine the area of the triangle below. Write your answer to the nearest hundredth.
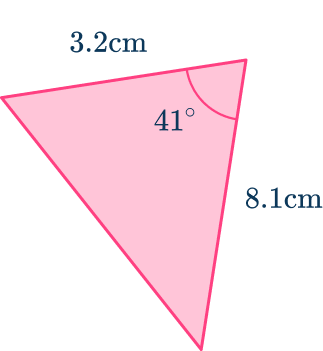




As you know the included angle between two side lengths, you can find the area of a triangle using sine where
and
Trig formulas FAQs
Here is a list of trig formulas you may need to know:
◦ Basic trigonometric formulas
◦ Inverse trigonometric formulas
◦ Trigonometry identities
◦ Reciprocal identities
◦ Periodic identities
◦ Co-function identities
◦ Sum and difference identities
◦ Double angle identities
◦ Triple angle identities
◦ Half angle identities
◦ Product identities
◦ Sum to product identities
The Pythagorean identity is a fundamental trigonometric identity that relates the squares of the sine and cosine of an angle. It is expressed as:
This identity states that for any angle the sum of the square of the sine of the angle and the square of the cosine of the angle always equals It is derived from Pythagoras’ theorem applied to a right triangle in the unit circle.
A trigonometry table is a chart that lists the values of trigonometric functions—such as sine, cosine, and tangent—for various angles, typically in degrees or radians. These tables were historically used to find the values of these functions before the widespread use of calculators.
Reciprocal identities are trigonometric identities that express each trigonometric function as the reciprocal of another function. For example:
◦ Secant or
◦ Cosecant or
◦ Cotangent or
The next lessons are
- Circle math
- Sectors arcs and segments
- Circle theorems
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!