A cuboid is a 3D shape that has [katex] 6 [/katex] rectangular sides. It is also known as rectangular prism.

Volume of a Prism - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Prism shape Area of a rectangle Area of a triangle Decimals Fractions

Math resources Geometry Volume

Volume of a prism

Here you will learn about the volume of a prism, including what it is and how to find it.

Students will first learn about the volume of a prism as part of geometry in $5$ th grade. Students will expand on this knowledge in $6$ th grade and $7$ th grade geometry.

What is the volume of a prism?

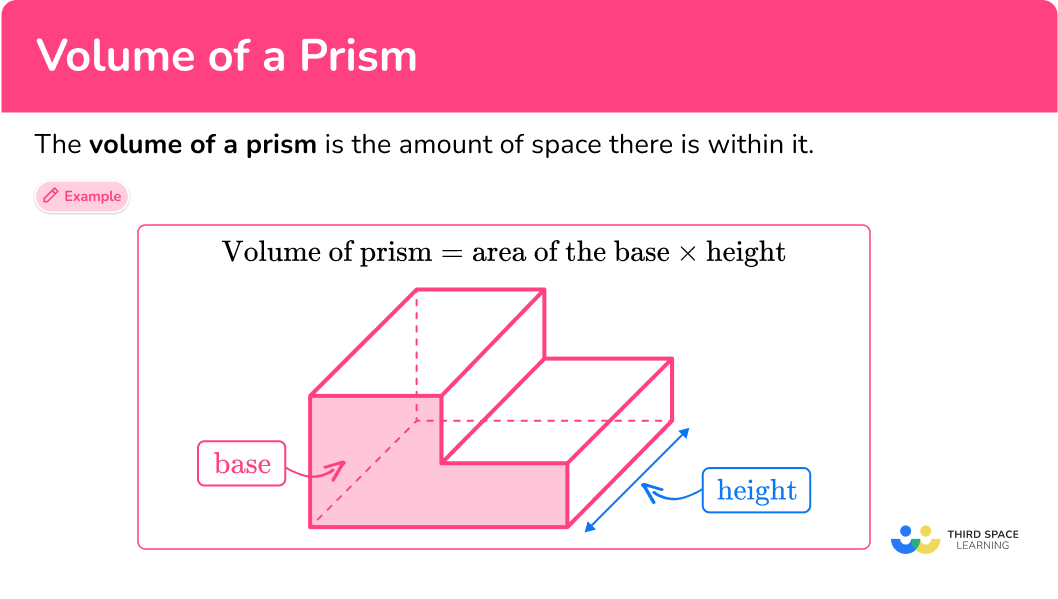
The volume of a prism is the amount of space there is within it.

$\text {Volume of prism }=\text { Area of the base } \times \text { height}$

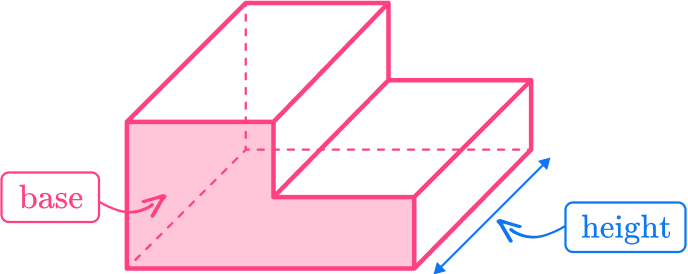
For example,

Imagine filling this L-shaped prism fully with water. The total amount of water inside the prism would represent the volume of the prism in cubic units.

To calculate the volume of any prism, we find the area of the base and multiply it by the height.

To identify the base of the prism, look for two opposite congruent sides that are connected by any number of lateral sides. For right prisms, the lateral sides are always rectangles.

What is the volume of a prism?

Common Core State Standards

How does this relate to $5$ th grade math and $6$ th grade math?

Grade 5 – Geometry (5.G.C.5b)
Apply the formulas $V=l \times w \times h$ and $V=b \times h$ for rectangular prisms to find volumes of right rectangular prisms with whole – number edge lengths in the context of solving real world and mathematical problems.

Grade 6 – Geometry (6.G.A.2)
Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes of the appropriate unit fraction edge lengths, and show that the volume is the same as would be found by multiplying the edge lengths of the prism.

Apply the formulas $V =l \times w \times h$ and $V = b \times h$ to find volumes of right rectangular prisms with fractional edge lengths in the context of solving real-world and mathematical problems.

Grade 7 – Geometry (7.G.B.6)
Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.

[FREE] Volume Check for Understanding Quiz (Grade 6 to 8)

Use this quiz to check your grade 6 to 8 students’ understanding of volume. 10+ questions with answers covering a range of 6th, 7th and 8th grade volume topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Volume Check for Understanding Quiz (Grade 6 to 8)

DOWNLOAD FREE

How to calculate the volume of a prism

In order to calculate the volume of a prism:

Write down the formula.
Calculate the area of the base.
Calculate the volume of the prism.
Write the answer, including the units.

Volume of a prism examples

Example 1: volume of a rectangular prism

A swimming pool is being built in the shape of a rectangular prism.

Calculate the volume of water in the pool when it is completely filled.

Write down the formula.

$\text {Volume of prism }=\text { Area of the base } \times \text { height}$

2Calculate the area of the base.

A rectangular prism has $3$ pairs of opposite, congruent faces. Any two opposite, congruent faces can serve as the base, making the height the edge perpendicular to the chosen base. In this case, use the front face as the base.

$\begin{aligned} \text{Area of rectangle }&= b\times{h} \\\\ &=12 \times {3} \\\\ &=36\end{aligned}$

The area of the rectangle is $36 \mathrm{~m}^2.$

3Calculate the volume of the prism.

The height of the prism is $5 \, m.$

$\begin{aligned} \text{Volume of prism }&= \text{Area of the base }\times{ height}\\\\ &=36\times{5}\\\\ &=180 \end{aligned}$

4Write the answer, including the units.

The measurements on this prism are in meters, so the volume is measured in cubic meters.

$\text {Volume }=180 \mathrm{~m}^3$

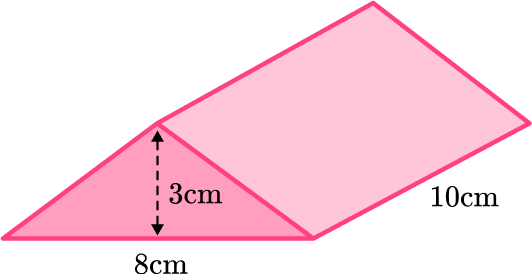
Example 2: volume of a triangular prism

Calculate the volume of the triangular prism:

Write down the formula.

$\text {Volume of prism }=\text { Area of the base } \times \text { height}$

Calculate the area of the base.

A triangular prism has two congruent triangular bases connected by lateral faces – so the base is the triangle.

$\begin{aligned} \text{Area of triangle }&=\cfrac{1}{2}\times{b}\times{h}\\\\ &=\cfrac{1}{2}\times{8}\times{3}\\\\ &=12 \end{aligned}$

The area of the triangle is $12 \mathrm{~cm}^2.$

Calculate the volume of the prism.

The height of the prism is $10 \, cm.$

$\begin{aligned} \text{Volume of prism }&= \text{Area of the base }\times{ height}\\\\ &=12\times{10}\\\\ &=120\\ \end{aligned}$

Write the answer, including the units.

The measurements on this triangular prism are in centimeters, so the volume is measured in cubic centimeters.

$\text {Volume }=120 \mathrm{~cm}^3$

Example 3: volume of a cube – fractions

Calculate the volume of the cube:

Write down the formula.

$\text {Volume of prism }=\text { Area of the base } \times \text { height}$

Calculate the area of the base.

$\begin{aligned} \text {Area of the square } &=s \times s \\\\ & =7 \, \cfrac{1}{3} \, \times 7 \, \cfrac{1}{3} \\\\ & =\cfrac{22}{3} \, \times \, \cfrac{22}{3} \\\\ & =\cfrac{484}{9} \\\\ & =53 \, \cfrac{7}{9} \end{aligned}$

Calculate the volume of the prism.

The height of the cube is $7 \, \cfrac{1}{3}.$

$\begin{aligned} \text {Volume of prism} &= \text {Area of the base} \times height \\\\ & =53 \, \cfrac{7}{9} \, \times 7 \, \cfrac{1}{3} \\\\ & =\cfrac{484}{9} \, \times \cfrac{22}{3} \\\\ & =\cfrac{10,648}{27} \\\\ & =394 \, \cfrac{10}{27}\end{aligned}$

Write the answer, including the units.

No unit is given, so the volume is written with general cubic units.

$\text { Volume }=394 \, \cfrac{10}{27} \text { units }^3$

Example 4: volume of a hexagonal prism

Calculate the volume of the prism:

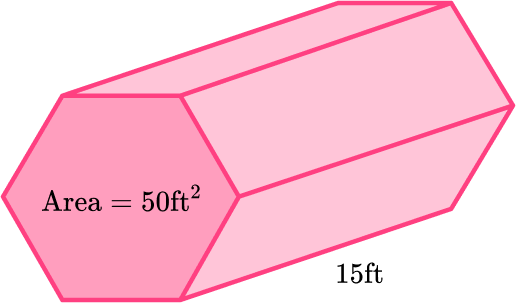
Write down the formula.

$\text { Volume of prism }=\text { Area of the base } \times \text { height }$

Calculate the area of the base.

A hexagonal prism has two congruent hexagonal bases connected by lateral faces – so the base is a hexagon. The area of the hexagon is $50 \, \mathrm{ft}^2.$

Calculate the volume of the prism.

The height of the prism is $15 \, ft.$

$\begin{aligned}\text{Volume of prism }&= \text{Area of the base }\times{ height}\\\\ &=50\times{15}\\\\ &=750\end{aligned}$

Write the answer, including the units.

The measurements on this prism are in feet, so the volume is measured in cubic feet.

$Volume = 750 \, \mathrm{ft}^3$

Example 5: volume of a compound prism

Calculate the volume of the L-shaped prism:

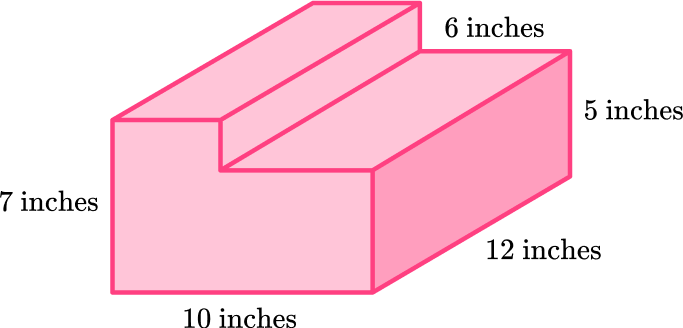
Write down the formula.

$\text {Volume of prism }=\text { Area of the base } \times \text { height}$

Calculate the area of the base.

To calculate the area of the base, split it into two rectangles and find the missing side lengths. Then calculate the area of each rectangle:

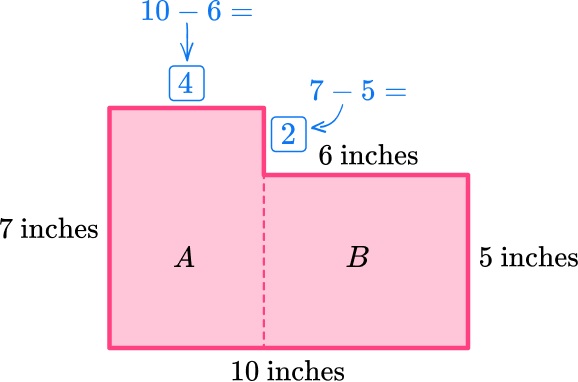
Rectangle $A$ :

$\begin{aligned} \text{Area } &=7\times{4}\\\\ &=28 \end{aligned}$

Rectangle $B$ :

$\begin{aligned}\text{Area } &=6\times{5}\\\\ &=30\end{aligned}$

Total area:

$28+30=58 \text { inches}^2$

Calculate the volume of the prism.

The height of the prism is $12$ inches.

$\begin{aligned} \text{Volume of prism }&= \text{Area of the base }\times{ height}\\\\ &=58\times{12}\\\\ &=696 \end{aligned}$

Write the answer, including the units.

The measurements on this prism are in inches, so the volume is measured in cubic inches.

$\text {Volume }=696 \text { inches}^3$

Example 6: missing length in a pentagonal prism

The volume of this prism is $225 \mathrm{~cm}^2$ . Calculate the height, $h$ , of the prism:

Write down the formula.

$\text {Volume of prism }=\text { Area of the base } \times \text { height}$

Calculate the area of the base.

A pentagonal prism has two congruent pentagonal bases connected by lateral faces – so the base is a pentagon. The area of the hexagon is $25 \mathrm{~cm}^2.$

Calculate the volume of the prism.

The volume and the base area are known, so fill them into the equation.

$225=25 \times h$

The height of the prism, $h$ , times $25$ is equal to $225$ . Solve the equation to find the value for $h$ that makes the equation true.

$\begin{aligned} & 225=25 \times h \\\\ & \div 25 \quad \div 25 \\\\ & 9=h \end{aligned}$

Write the answer, including the units.

The height of the prism is $9 \, cm.$ Remember, since the height is a side length – it is 2D and therefore measured in units (not units squared or cubed).

Teaching tips for volume of a prism

Before having students calculate the volume of prisms on worksheets, make sure they have opportunities to identify and work with physical prisms. This can be through the use of math manipulatives or activities that involve real world prisms.

Give students a hands-on understanding of volume by having them build different rectangular or composite prisms out of cubes (such as centimeter cubes that come in base $10$ block sets or with linking cubes).

Easy mistakes to make

Writing the incorrect units or no units at all
Volume is always measured in cubed units. Writing volume as square units or not including any units does not accurately represent what volume is measuring.
For example,
The volume of the prism is…

$\bf{36}$ ✘	$\bf{36}$ units $\bf{^2}$ ✘	$\bf{36}$ units $\bf{^3}$ ✔
There is no indication of what is being measured here… $36$ feet? $36$ ropes? $36$ dogs? This does not show volume or any other unit.	Square units are a $2$ -dimensional measurement for area, like this rectangle: This does not show volume.	There are $36$ cubed units that make up this $3$ -dimensional prism. This shows volume.

Calculating with different units
All measurements need to be in the same units before calculating volume.

Using the incorrect formula
Be careful to apply the correct formula to find the area of the base of the prism – as they are not the same for different shapes. Also make sure that the dimensions used for the height of the prism is perpendicular to the base.

Practice volume of a prism questions

192 \mathrm{~cm}^3

48 \mathrm{~cm}^3

96 \mathrm{~cm}^3

40 \mathrm{~cm}^3

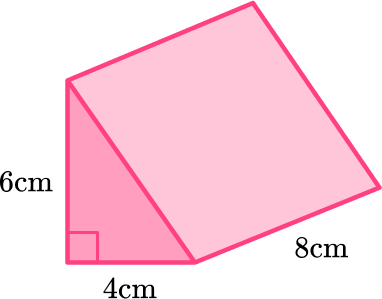
This is a triangular prism and the bases are two identical triangles.

First calculate the area of the base.

$\begin{aligned} \text{Area of triangle }&=\cfrac{1}{2} \, \times 4 \times 6\\\\ &=12 \, \mathrm{cm}^{2} \end{aligned}$

Then multiply the area of the base times the height of the prism.

$\begin{aligned} \text{Volume of triangular prism }&=12 \times 8\\\\ &=96 \, \mathrm{cm}^{3} \end{aligned}$

6 \cfrac{1}{18} \, \mathrm{ft}^3

6 \cfrac{5}{9} \, \mathrm{ft}^3

15 \cfrac{1}{9} \, \mathrm{ft}^3

15 \cfrac{5}{9} \, \mathrm{ft}^3

Any two opposite congruent faces can be used as the base of the rectangular prism. Let’s solve it with the bottom face as the base.

First, calculate the area of the base.

$\begin{aligned} \text { Area of rectangle }&= 2 \times 2 \cfrac{1}{2} \\\\ & =\cfrac{2}{1} \, \times \cfrac{5}{2} \\\\ & =\cfrac{10}{2} \\\\ & =5 \, f t^2 \end{aligned}$

Then multiply the area of the base times the height of the prism.

$\begin{aligned} \text {Volume of rectangular prism } & =5 \times 3 \, \cfrac{1}{9} \\\\ & =\cfrac{5}{1} \, \times \cfrac{28}{9} \\\\ & =\cfrac{140}{9} \\\\ & =15 \, \cfrac{5}{9} \, f t^3 \end{aligned}$

240 \mathrm{~m}^3

2.4 \mathrm{~m}^3

2,400 \mathrm{~m}^3

5,760 \mathrm{~m}^3

This is a pentagonal prism and the bases are two identical pentagons.

The area of the pentagonal base is given: $24 \mathrm{~m}^2.$

The height of the prism is $10 \, m.$

$\begin{aligned} \text{Volume of prism }&=24 \times 10 \\\\ &=240 \, \mathrm{m}^{3} \end{aligned}$

84 \mathrm{~cm}^3

1,008 \mathrm{~cm}^3

1,008 \mathrm{~cm}^3

1,344 \mathrm{~cm}^3

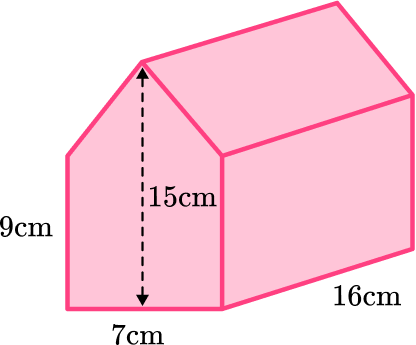
The base of this pentagonal prism can be broken up into a triangle and a rectangle.

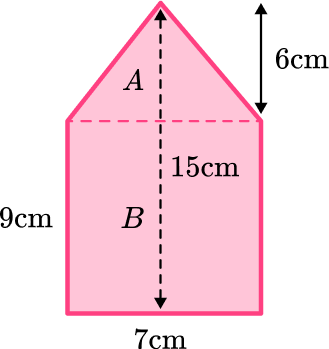
Volume of a Prism image 15 US

Area of triangle $A$ :

$\begin{aligned} \text{Area }&=\cfrac{1}{2} \, \times 7 \times 6\\\\ &=21 \, \mathrm{cm}^{2} \end{aligned}$

Area of rectangle $B$ :

$\begin{aligned} \text{Area }&=7 \times 9 \\\\ &=63 \, \mathrm{cm}^{2} \end{aligned}$

$\text{Total area: } 21+63=84 \, \mathrm{cm}^{2}$

The height of the prism is $16 \, cm.$

$\begin{aligned} \text{Volume of prism }&=84 \times 16 \\\\ &=1,344 \, \mathrm{cm}^{3} \end{aligned}$

1,872 \, cm

13 \, cm

1.08 \, cm

6.5 \, cm

$\text {Volume of prism }=\text { Area of the base } \times \text { height }$

The total volume is $156 \mathrm{~cm}^3$ and the area of the base is $12 \mathrm{~cm}^2$ – fill those into the formula.

$156=12 \, x$

The height of the base, $x,$ times $12$ is equal to $156.$ Solve the equation to find the value for $x$ that makes the equation true.

$\begin{aligned} & 156=12 x \\\\ & \div 12 \; \div 12 \\\\ & 13=x \end{aligned}$

The height of the prism is $13 \, cm.$ Remember, since the height is a side length – it is 2D and therefore measured in units (not units squared or cubed).

12,150 \, mm

30 \, mm

6 \, mm

45 \, mm

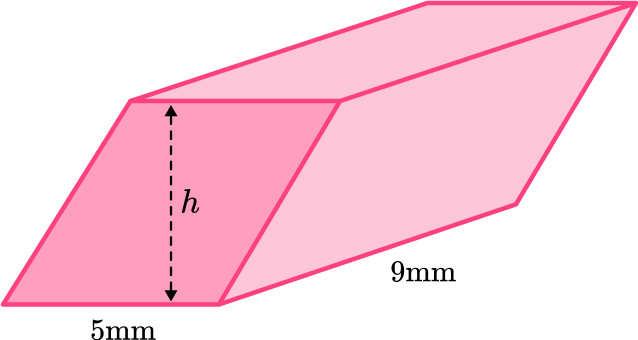
All the faces of this prism are parallelograms. Any two opposite congruent faces can be used as the base. Let’s use the bottom face.

$\begin{aligned} \text { Area of parallelogram } & =5 \times 9 \\\\ & =45 \end{aligned}$

$\text {Volume of prism }=\text { Area of the base } \times \text { height }$

The total volume is $270 \, mm^3$ and area of the base is $45 \, mm^2$ – fill those into the formula.

$270=45 \times h$

The height of the prism, $h,$ times $45$ is equal to $270.$ Solve the equation to find the value for h that makes the equation true.

$\begin{aligned} & 270=45 h \\\\ & \div 45 \; \div 45 \\\\ & h=6 \end{aligned}$

The height of the prism is $6 \, mm.$ Remember, since the height is a side length – it is 2D and therefore measured in units (not units squared or cubed).

Volume of a prism FAQs

Are there other types of prisms not shown on this page?

Yes, there are many types of prisms that are not included on this page. Any shape that has two identical polygonal bases connected by lateral faces is a prism. The shape of the base of a prism is how it is named. For example, a prism with two congruent trapezoids connected by lateral faces is called a trapezoidal prism.

What is a cuboid?

A cuboid is a 3D shape that has $6$ rectangular sides. It is also known as rectangular prism.

How do you calculate the volume of a cylinder?

Even though a cylinder is not a prism, because it has two congruent bases and a consistent height throughout, it is also found by multiplying the area of the base and the height of the cylinder.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.