High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Multiplying fractions Area of a circle Rounding Volume Volume of a sphereVolume of a hemisphere
Here you will learn about the volume of a hemisphere, including what a hemisphere is and how to calculate the volume of a hemisphere given the radius or the diameter.
Students will first learn about the volume of a hemisphere as part of geometry in 8 th grade, then expand their learning in high school.
What is the volume of a hemisphere?
The volume of a hemisphere is the amount of space inside a hemisphere.
To calculate the volume of a hemisphere, you need to know what a hemisphere is. “Hemi” means half, so a hemisphere is half of a sphere. It is a three dimensional shape, with a radius, r.
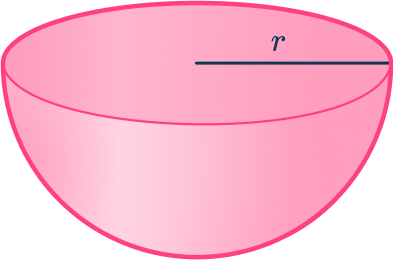
To calculate the volume of a full sphere, where r is the radius of the sphere, you use the formula
V=\cfrac{4}{3} \, \pi{r^3}
Since a hemisphere is half of a sphere, to find the volume of a hemisphere you halve the volume of a sphere.
Here is the volume of a hemisphere formula, with radius r.
V=\cfrac{4}{3} \, \pi{r^3}\div{2}
Or, alternatively,
\begin{aligned}\text {Volume of a hemisphere}&=\cfrac{1}{2}\times\cfrac{4}{3} \, \pi{r^3} \\\\ &=\cfrac{2}{3} \, \pi{r^3} \end{aligned}
What is the volume of a hemisphere?

Common Core State Standards
How does this relate to 8 th grade math and high school math?
- Grade 8 – Geometry (8.G.C.9)
Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.
- High School – Geometry (HS.G.GMD.A.3)
Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.
![[FREE] Volume Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Volume-check-for-understanding-quiz-listing-image.png)
[FREE] Volume Worksheet (Grade 6 to 8)
![[FREE] Volume Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Volume-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 6 to 8 students’ understanding of volume. 10+ questions with answers covering a range of 6th, 7th and 8th grade volume topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Volume Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Volume-check-for-understanding-quiz-listing-image.png)
[FREE] Volume Worksheet (Grade 6 to 8)
![[FREE] Volume Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Volume-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 6 to 8 students’ understanding of volume. 10+ questions with answers covering a range of 6th, 7th and 8th grade volume topics to identify areas of strength and support!
DOWNLOAD FREEHow to calculate the volume of a hemisphere
In order to calculate the volume of a hemisphere:
- Write down the formula for the volume of a hemisphere.
- Substitute in the known variables.
- Solve for the unknown variable.
Volume of a hemisphere examples
Example 1: radius is given
Calculate the volume of a hemisphere with radius 4.5\mathrm{~cm}. Give your answer to the nearest tenth.
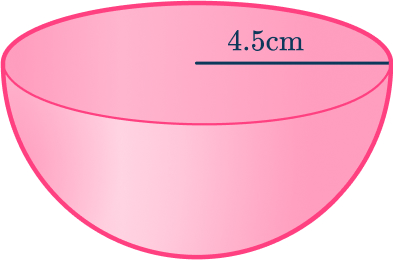
- Write down the formula for the volume of a hemisphere.
The formula for finding the volume of a hemisphere is
V=\cfrac{4}{3} \, \pi{r^3}\div{2}2Substitute in the known variables.
V=\cfrac{4}{3} \, \pi (4.5)^3\div 23Solve for the unknown variable.
Using a calculator, V=190.9\mathrm{~cm}^3 (nearest tenth)
Example 2: diameter of a hemisphere is given
Calculate the volume of a hemisphere with diameter 12.3\mathrm{~mm}. Give your answer to the nearest tenth.
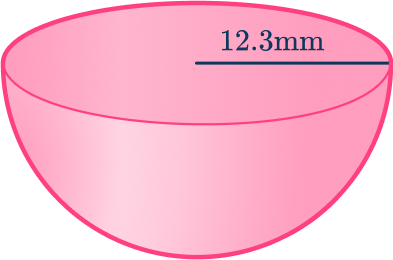
Write down the formula for the volume of a hemisphere.
The formula for finding the volume of a hemisphere is
V=\cfrac{2}{3} \, \pi{r^3}
Substitute in the known variables.
You have been given the diameter. As the diameter is double the length of the radius, you need to halve 12.3 to get the radius of the hemisphere.
r=12.3\div{2}=6.15
Now, V=\cfrac{2}{3} \, \pi(6.15)^3
Solve for the unknown variable.
Using a calculator, V=487.2\mathrm{~mm}^3 (nearest tenth)
Example 3: leaving answer in terms of π, radius given
Calculate the volume of a hemisphere with radius 6\mathrm{~km}. Leave your answer in terms of \pi.
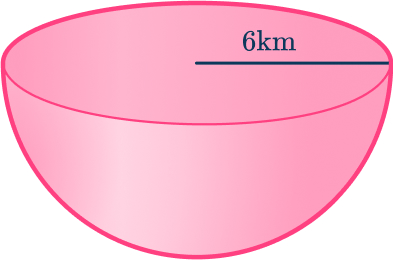
Write down the formula for the volume of a hemisphere.
The formula for finding the volume of a hemisphere is
V=\cfrac{4}{3} \, \pi{r^3}\div{2}
Substitute in the known variables.
Solve for the unknown variable.
Using a calculator, V=144 \, \pi\mathrm{~km}^3
Example 4: leaving answer in terms of π, diameter of a hemisphere is given
Calculate the volume of a hemisphere with diameter 6\mathrm{~m}. Leave your answer in terms of \pi.
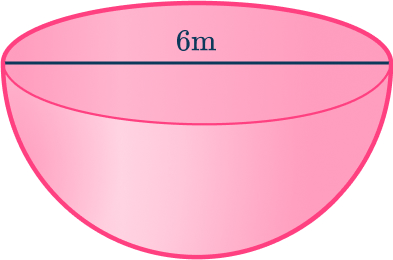
Write down the formula for the volume of a hemisphere.
The formula for finding the volume of a hemisphere is
V=\cfrac{2}{3} \, \pi{r^3}
Substitute in the known variables.
You have been given the diameter. You need to halve 6 to get the radius.
r=6\div{2}=3
Now, V=\cfrac{2}{3} \, \pi(3)^3=\cfrac{2}{3}\times\pi\times{27}
Solve for the unknown variable.
Without a calculator,
27\times\cfrac{2}{3}=27\times{2}\div{3}=54\div{3}=18
So V=18 \, \pi\mathrm{~m}^3
Example 5: finding the radius, given the volume
The volume of a hemisphere is 500\mathrm{~cm}^3. Calculate the radius. Give your answer to the nearest hundredth.
Write down the formula for the volume of a hemisphere.
The formula for finding the volume of a hemisphere is
V=\cfrac{2}{3} \, \pi{r^3}
Substitute in the known variables.
You can substitute in the value of the volume.
500=\cfrac{2}{3} \, \pi{r^3}
Solve for the unknown variable.
Rearrange the equation to calculate the radius.
Example 6: finding the diameter, given the volume
The volume of a hemisphere is 400\mathrm{~cm}^3. Calculate the diameter. Give your answer to the nearest tenth.
Write down the formula for the volume of a hemisphere.
The formula for finding the volume of a hemisphere is
V=\cfrac{4}{3} \, \pi{r^3}\div{2}
Substitute in the known variables.
Substitute in the value of the volume
400=\cfrac{4}{3} \, \pi{r^3}\div{2}
Solve for the unknown variable.
Rearrange the equation to find the radius.
This gives the radius as 5.7588…, which needs to be doubled to find the diameter.
d=5.7588…\times{2}=11.52\mathrm{~cm} (nearest hundredth)
Example 7: finding the capacity of a hemisphere
A basin is filled with water. The basin is a hemisphere with a radius of 30\mathrm{~cm}. Find the capacity of the hemisphere in liters.
Write down the formula for the volume of a hemisphere.
The formula for finding the volume of a hemisphere is
V=\cfrac{2}{3} \, \pi{r^3}
Substitute in the known variables.
Substitute in the value of the radius to find the volume
V=\cfrac{2}{3} \, \pi\times(30)^3
Solve for the unknown variable.
Using a calculator, V=56548.66776…\mathrm{~cm}^3. As 1L=1000\mathrm{~cm}^3, divide the volume by 1000 to determine the capacity in liters.
56548.66776\div{1000}=56.549\mathrm{~L}
Teaching tips for volume of a hemisphere
- Start by introducing real life examples of hemispheres, such as a dome, igloo, or even the northern and southern hemispheres of earth. This helps students visualize the shape and understand its relevance.
- Use visual aids such as diagrams and physical models to help students visualize a hemisphere and its volume. Showing them how slicing a sphere into two equal halves can make the idea more concrete.
- Provide worksheets with a variety of practice problems at different difficulty levels. Include problems that involve finding the volume of a hemisphere given the radius, as well as word problems and real life applications.
Easy mistakes to make
- Using the incorrect formula
There are several formulas relating to circles that can be confused so make sure you learn the difference between them.
- Rounding the answer too early
It is important to wait to round the answer until the end of the calculation. It is useful to keep your answer in terms of \pi until you round the answer at the very end of the question.
- Writing the incorrect units
For area, you use square units such as square centimeters. You can write this with an exponent as cm^2.
For volume, you use cubic units such as cubic centimeters. You can write this with an exponent as cm^3.
- Mixing up the radius and diameter
It is a common error to mix up radius and diameter. Remember the radius is half of the diameter.
Practice volume of a hemisphere questions
1. Find the volume of a hemisphere with radius 7.9\mathrm{~cm}. Give your answer correct to the nearest tenth.
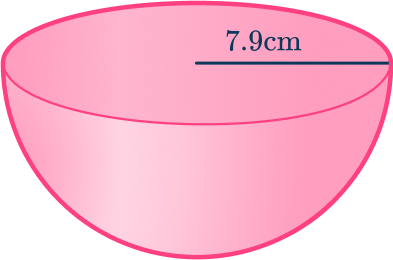




The volume of the hemisphere can be found by using the volume of a sphere and halving it.
\begin{aligned}V&=\cfrac{4}{3} \, \pi{r^3}\div{2} \\\\ V&=\cfrac{4}{3} \, \pi(7.9)^3\div{2} \\\\ V&=1032.618… \\\\ V&=1032.6\mathrm{~cm}^3\text{ (nearest tenth)} \end{aligned}
2. Find the volume of a hemisphere with diameter 4.6\mathrm{~m}. Give your answer correct to the nearest tenth.
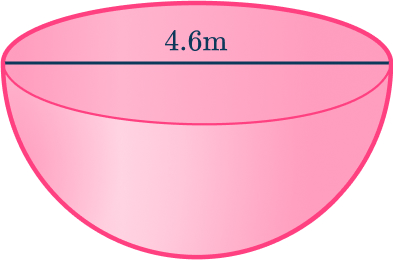




First you need to divide the diameter by 2 to find the radius. The radius is 2.3\mathrm{~m}. The volume of the hemisphere can be found by using the volume of a sphere and halving it.
\begin{aligned}V&=\cfrac{2}{3} \, \pi{r^3} \\\\ V&=\cfrac{2}{3} \, \pi(2.3)^3 \\\\ V&=25.4825… \\\\ V&=25.5\mathrm{~m}^3\text{ (nearest tenth)} \end{aligned}
3. Find the volume of a hemisphere with radius 10\mathrm{~mm}. Leave your answer in terms of \pi.
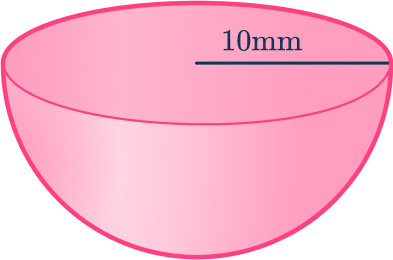




The volume of the hemisphere can be found by using the volume of a sphere and halving it.
\begin{aligned}V&=\cfrac{4}{3} \, \pi{r^3}\div{2} \\\\ V&=\cfrac{4}{3} \, \pi(10)^3\div{2} \\\\ V&=\cfrac{2000}{3} \, \pi \\\\ V&=\cfrac{2000}{3} \, \pi\mathrm{~mm}^3 \end{aligned}
4. Find the volume of a hemisphere with diameter 4\mathrm{~km}. Leave your answer in terms of \pi.
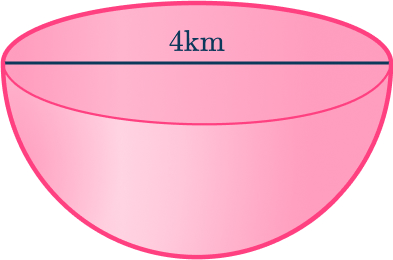




First you need to divide the diameter by 2 to find the radius. The radius is 2 \, km. The volume of the hemisphere can be found by using the formula:
\begin{aligned}V&=\cfrac{2}{3} \, \pi{r^3} \\\\ V&=\cfrac{2}{3} \, \pi(2)^3 \\\\ V&=\cfrac{16}{3} \, \pi \\\\ V&=\cfrac{16}{3} \, \pi\mathrm{~km}^3 \end{aligned}
5. A hemisphere has a volume of 1500\mathrm{~cm}^3. Calculate its radius. Give your answer correct to the nearest hundredth.




Equate the volume of a hemisphere to the given volume.
\begin{aligned}1500&=\cfrac{2}{3} \, \pi{r^3} \\\\ 4500&=2 \, \pi{r^3} \\\\ 2250&=\pi{r^3} \\\\ \cfrac{2250}{\pi}&=r^{3} \\\\ r&=\sqrt[3]{\cfrac{2250}{\pi}} \\\\ r&=8.94700… \\\\ r&=8.95\mathrm{~cm}\text{ (nearest hundredth)} \end{aligned}
6. A hemisphere has a volume of 2300\mathrm{~cm}^3. Calculate its diameter. Give your answer correct to the nearest tenth.




Form an equation by substituting the volume into the formula for the volume of a hemisphere and solve it to find the radius. Finally, you multiply the radius by 2 to find the diameter.
\begin{aligned}2300&=\cfrac{4}{3} \, \pi{r^3}\div{2} \\\\ 4600&=\cfrac{4}{3} \, \pi{r^3} \\\\ 13800&=4 \, \pi{r^3} \\\\ 3450&=\pi{r^3} \\\\ \cfrac{3450}{\pi}&=r^3 \\\\ r&=\sqrt[3]{\cfrac{3450}{\pi}} \\\\ r&=10.317… \end{aligned}
\begin{aligned} d&=r\times{2}\\\\ &=10.317…\times{2}\\\\ &=20.6\mathrm{~cm}\text{ (nearest tenth)} \end{aligned}
7. The capacity of a garden water feature is 20\mathrm{~L}. The water feature is a hemisphere. Determine the radius of the water feature to the nearest hundredth.




Convert liters to cubic centimeters first: 20\mathrm{~L}=20~000\mathrm{~cm}^3
\begin{aligned}V&=\cfrac{2}{3} \, \pi{r^3} \\\\ 20~000&=\cfrac{2}{3} \, \pi\times{r^3} \\\\ 60~000&=2 \, \pi\times{r^3} \\\\ 30~000&=\pi\times{r^3} \\\\ \cfrac{30~000}{\pi}&=r^{3} \\\\ \sqrt[3]{\cfrac{30~000}{\pi}}&=r \\\\ r&=21.22\mathrm{~cm}\text{ (nearest hundredth)} \end{aligned}
Volume of a hemisphere FAQs
A hemisphere is a 3D shape that looks like half of a sphere. It has a flat circular base and a curved surface extending from the base in all directions.
To find the volume of a hemisphere, you can use the formula for half of the volume of a sphere: V=\cfrac{2}{3} \, \pi{r^3}
The volume of a hemisphere measures the amount of space enclosed by its curved surface and base, calculated using the formula V=\cfrac{2}{3} \, \pi{r^3}.
The curved surface area of a hemisphere refers only to the area of its curved surface, excluding the base. It is calculated using the formula A=2 \, \pi{r^2}.
The next lessons are
- Surface area
- Pythagorean Theorem
- Trigonometry
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!