Quadrilateral Angles - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Quadrilateral Types of quadrilaterals Types of angles Angles of a triangle Straight angle Vertical angles theorem Parallel angles

Math resources Geometry

Angles in polygons

Quadrilateral angles

Here you will learn about quadrilateral angles, including the sum of quadrilateral angles, how to find missing angles, and how to use these angle facts to generate equations and solve problems.

Students will first learn about quadrilateral angles as part of geometry in high school.

What are quadrilateral angles?

Quadrilateral angles are the four angles that occur at each vertex within a four-sided shape; these angles are called interior angles of a quadrilateral.

The sum of the interior angles of a quadrilateral is $360^{\circ}.$ You can prove this using the angle sum of a triangle.

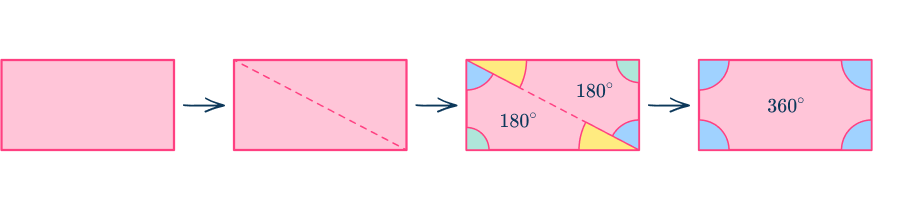
The rectangle above is split into two triangles by joining two vertices together across the diagonal. As the sum of angles in a triangle is $180^{\circ},$ you can add two lots of $180^{\circ}$ together, making the angle sum of a quadrilateral equal to $360^{\circ}.$

This is the same for all types of quadrilaterals:

Step-by-step guide: Angles of a triangle

What are quadrilateral angles?

[FREE] Angles Check for Understanding Quiz (Grade 4)

Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Angles Check for Understanding Quiz (Grade 4)

Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!

DOWNLOAD FREE

Angle properties of quadrilaterals

The four angles in any quadrilateral always add to $360^{\circ},$ but there are a few key properties of quadrilaterals that can help us calculate other angles.

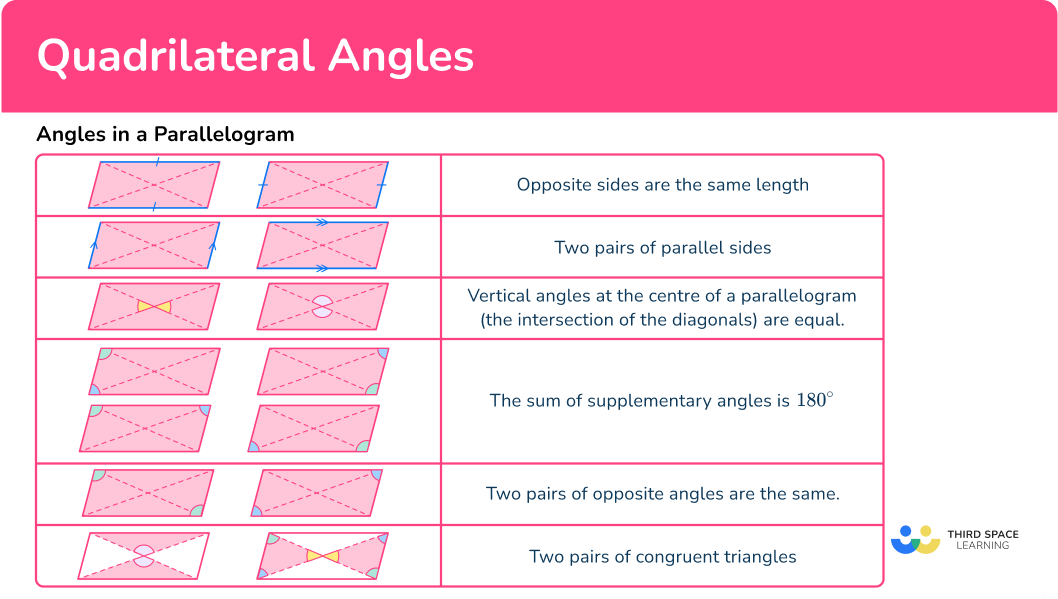
Parallelogram

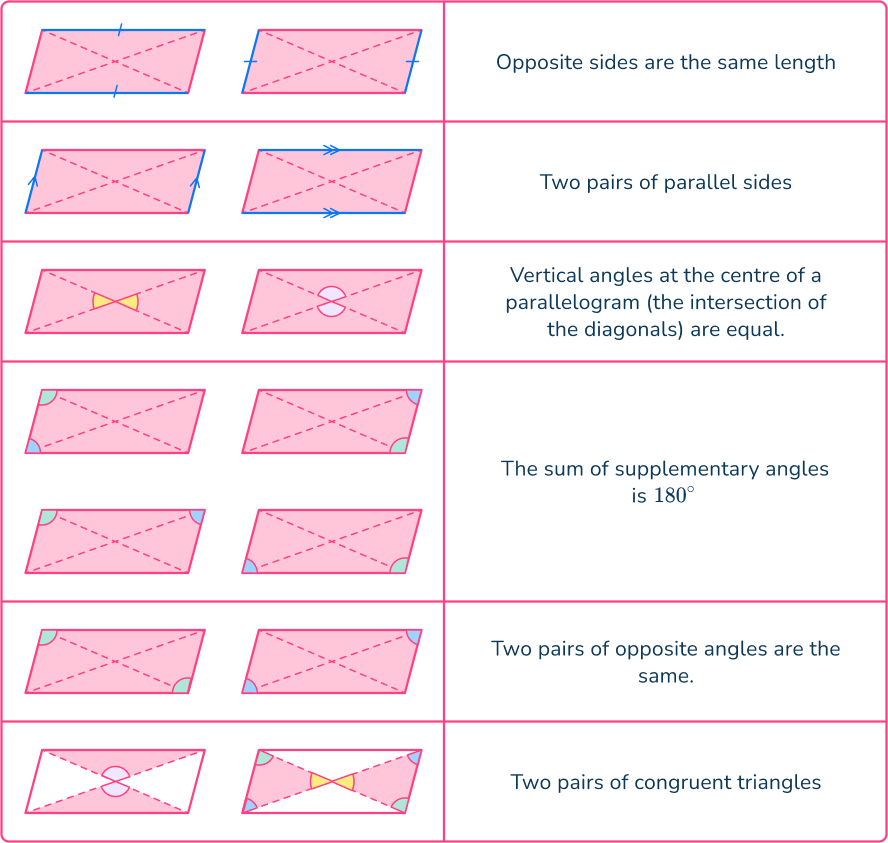
What are angles in a Parallelogram?

Rectangle

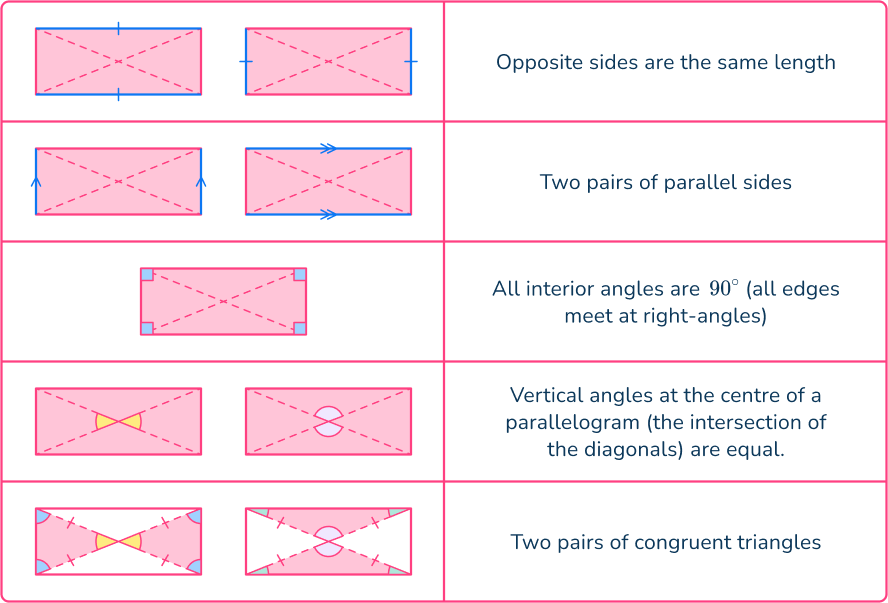
What are angles in a Rectangle?

Kite

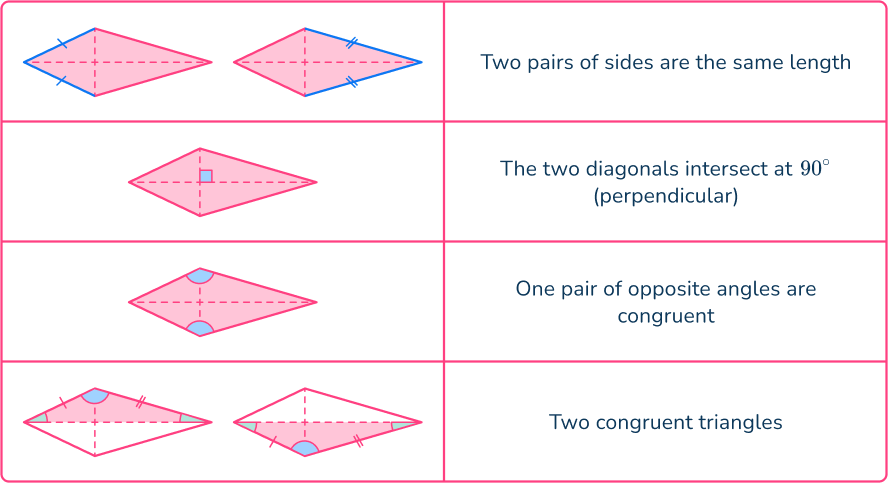
What are angles in a Kite?

Rhombus

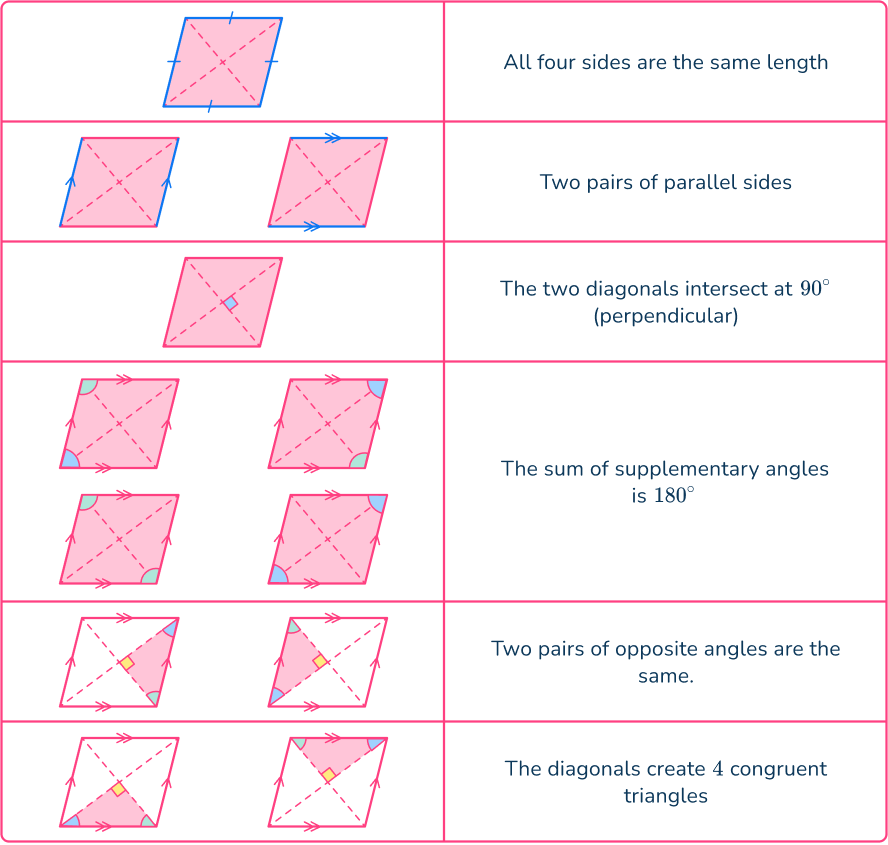
What are angles in a Rhombus?

Square

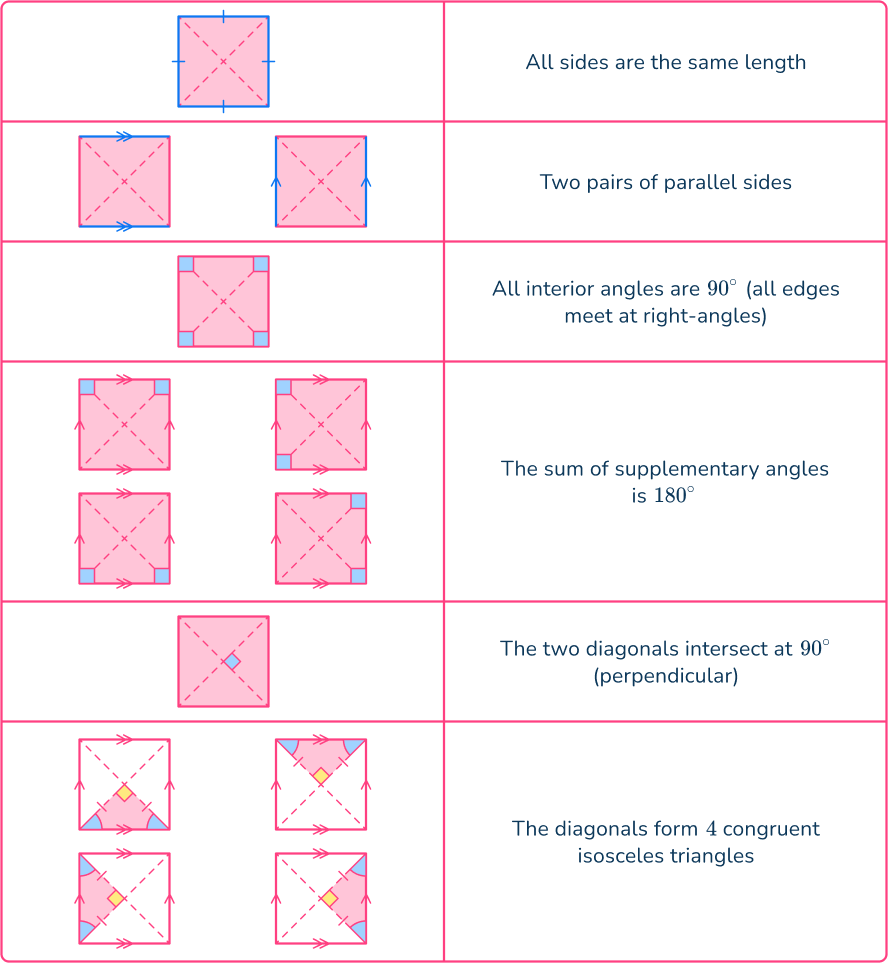
What are angles in a Square?

Trapezoid

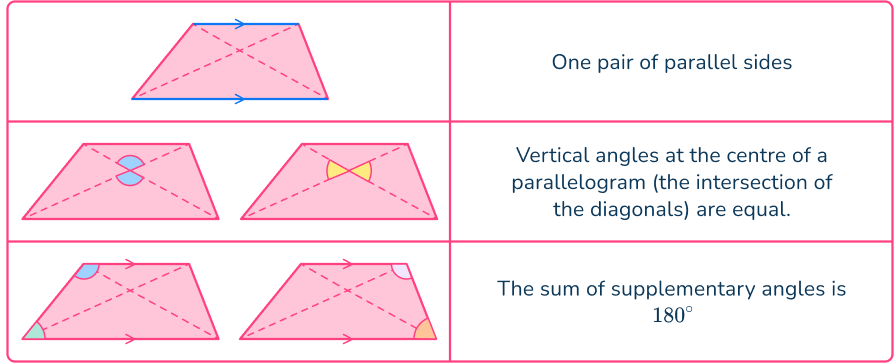
What are angles in a Trapezoid?

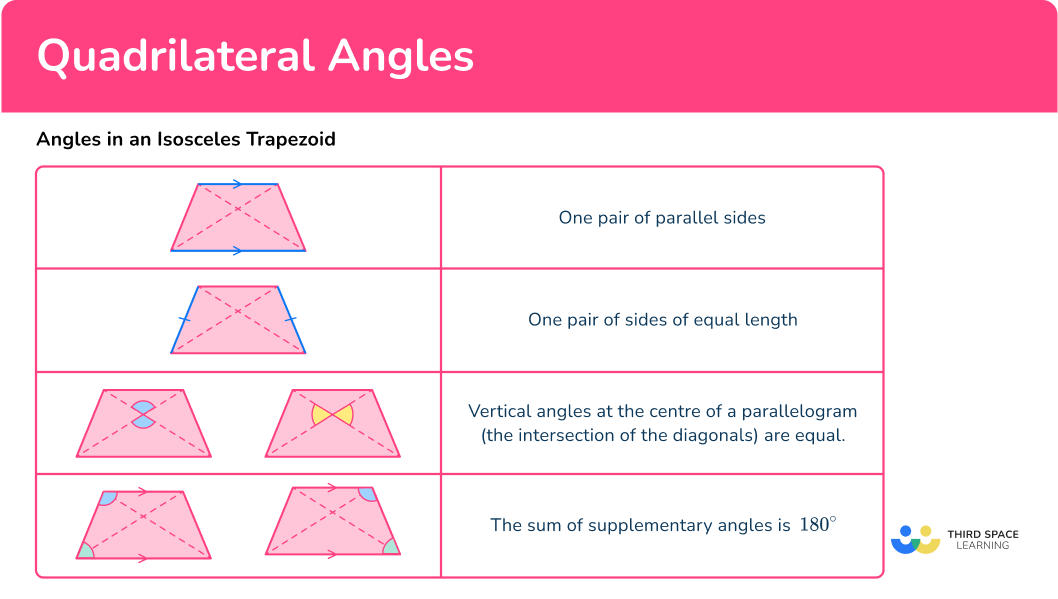
Isosceles trapezoid

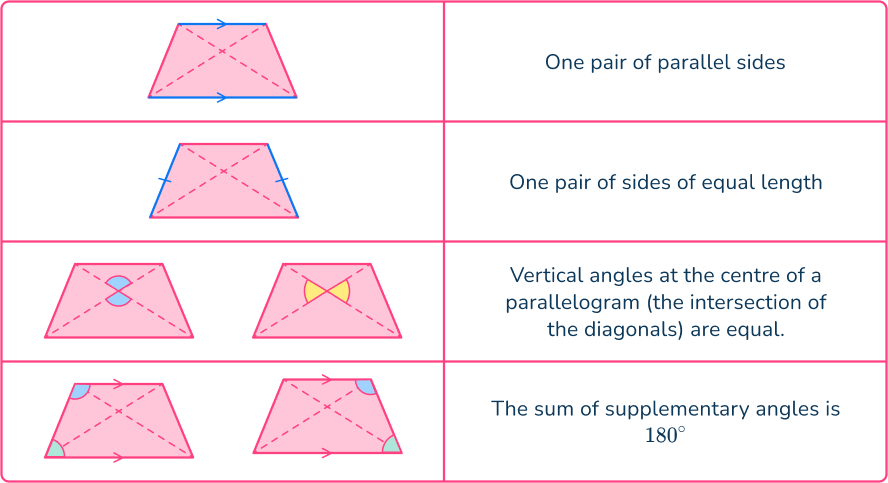
What are angles in an Isosceles Trapezoid?

Arrowhead

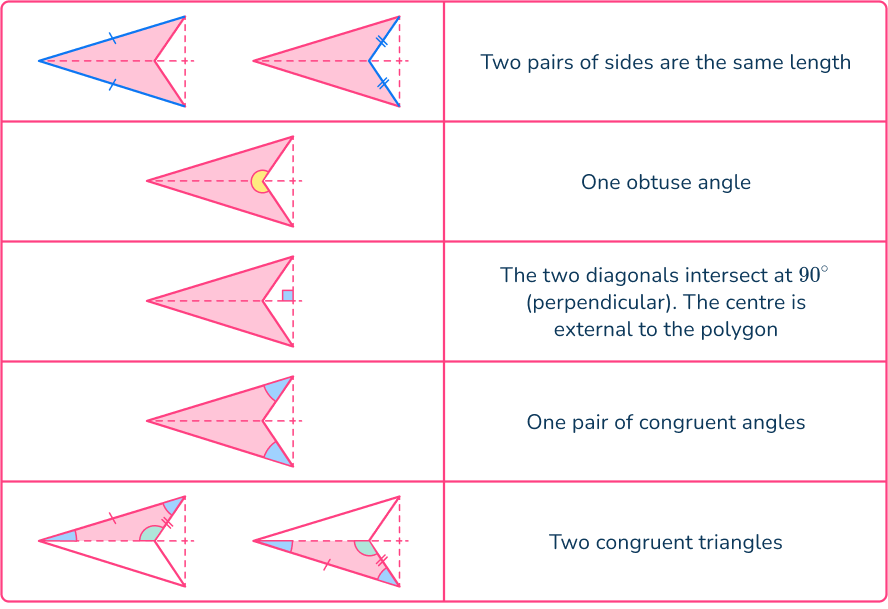
What are angles in an Arrowhead?

Common Core State Standards

How does this relate to high school math?

High School – Geometry – Congruence (H.G.CO.C.11)
Prove theorems about parallelograms. Theorems include: opposite sides are congruent, opposite angles are congruent, the diagonals of a parallelogram bisect each other, and conversely, rectangles are parallelograms with congruent diagonals.

How to find missing quadrilateral angles

In order to find missing quadrilateral angles:

Use angle properties to determine any interior angles.
Add all known interior angles.
a: Subtract the angle sum from $\bf{360}^{\circ}.$
b: Form and solve the equation.

Quadrilateral angles examples

Example 1: trapezoid

$ABCD$ is a trapezoid. Calculate the size of angle $BCD,$ labeled $x.$

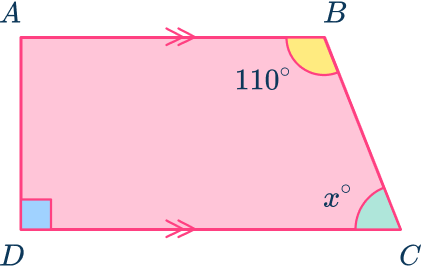
Use angle properties to determine any interior angles.

Angle fact:

The line $AD$ is perpendicular to lines $AB$ and $CD$ , so angle $BAD=90^{\circ}.$

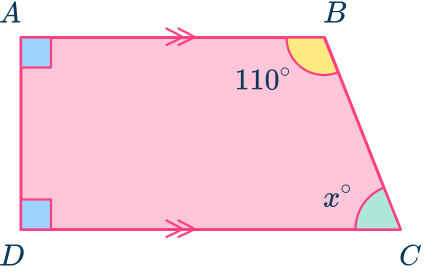
2Add all known interior angles.

90+90+110=290^{\circ}

3a: Subtract the angle sum from $\bf{360}^{\circ}.$

Here, $360-290=70^{\circ}$

So $x=70^{\circ}.$

Example 2: irregular quadrilateral

Find the value of the missing angle $x.$

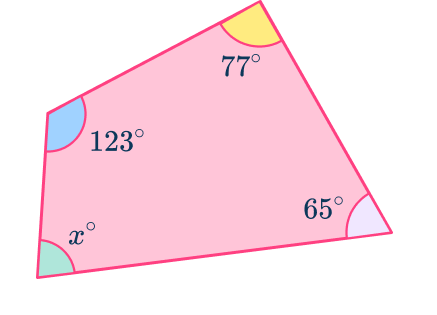
Use angle properties to determine any interior angles.

Angle fact:

Quadrilateral angles add to equal $360^{\circ}.$

Add all known interior angles.

123+77+65=265^{\circ}

a: Subtract the angle sum from $\bf{360}^{\circ}.$

Here, $360-265=95^{\circ}$

So $x=95^{\circ}.$

Example 3a: parallelogram with one interior angle (form and solve)

Calculate the missing angle for the following parallelogram.

Use angle properties to determine any interior angles.

Angle fact:

Co-interior angles add to equal $180^{\circ}.$

Add all known interior angles.

x+32

b: Form and solve the equation.

Here,

$\begin{aligned}x+32&=180 \\\\ x+32-32&=180-32 \\\\ x&=148^{\circ} \end{aligned}$

Example 3b: parallelogram with one interior angle (form and solve)

Calculate the missing angle for the following parallelogram.

Use angle properties to determine any interior angles.

Angle fact:

Diagonally opposite angles in a parallelogram are equal.

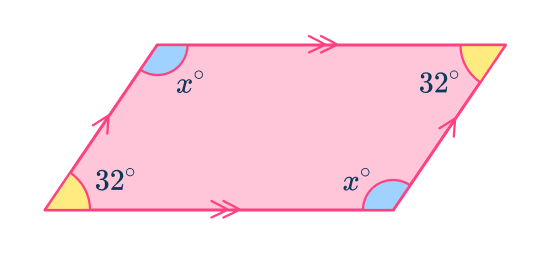
Add all known interior angles.

x+32+x+32.

Simplify this to get $2x+64.$

b: Form and solve the equation.

Here,

$\begin{aligned}2x+64&=360 \\\\ 2x+64-64&=360-64 \\\\ 2x&=296 \\\\ 2x\div{2}&=296\div{2} \\\\ x&=148^{\circ} \end{aligned}$

Example 4: exterior angle given

Calculate the measure of the missing angle for the following quadrilateral.

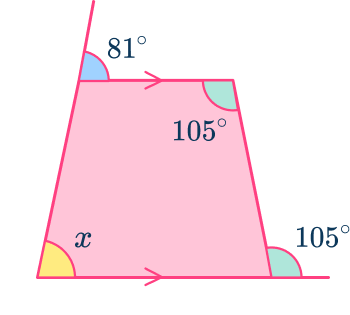
Use angle properties to determine any interior angles.

Angle fact:

Angles on a straight line add to equal $180^{\circ}.$

Add all known interior angles.

99+105+75=279

a: Subtract the angle sum from $\bf{360}^{\circ}.$

Here, $360-279=81^{\circ}$

So $x=81^{\circ}.$

Example 5: forming and solving equations

By finding the value for $x,$ calculate the value of each angle in the kite drawn below.

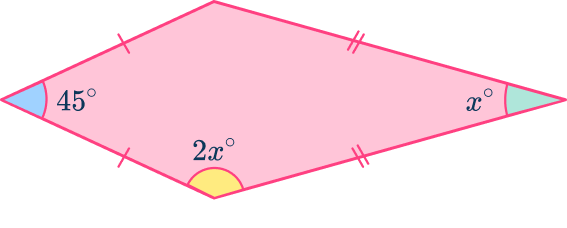
Use angle properties to determine any interior angles.

Angle fact:

One pair of diagonally opposite angles in a kite are the same size.

Add all known interior angles.

45+2x+x+2x.

Simplify this to get $5x+45.$

b: Form and solve the equation.

Here,

$\begin{aligned}5x+45&=360 \\\\ 5x+45-45&=360-45 \\\\ 5x&=315 \\\\ 5x\div{5}&=315\div{5} \\\\ x&=63^{\circ} \end{aligned}$

As $x=63^{\circ}$ , we can find the value for the remaining angles in the kite by substituting the value onto each angle:

$2x=2\times{63}=126^{\circ}$

So we have the four angles: $45^{\circ}, 126^{\circ}, 126^{\circ},$ and $63^{\circ}.$

You can check the solution by adding these angles together. They should add to equal $360.$

$45+126+126+63=360^{\circ}.$

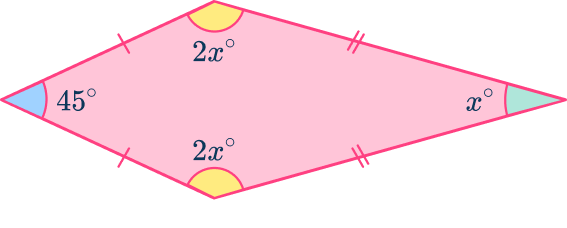
Example 6: forming and solving equations

By finding the value for $x,$ calculate the value of each angle in the quadrilateral.

Use angle properties to determine any interior angles.

For an irregular quadrilateral, there is only one angle property.

Quadrilateral angles add to equal $360^{\circ}.$

Add all known interior angles.

100+2x-30+5x+40+3x

This simplifies to be $10x+110.$

b: Form and solve the equation.

Here,

$\begin{aligned}10x+110&=360 \\\\ 10x+110-110&=360-110 \\\\ 10x&=250 \\\\ 10x\div{10}&=250\div{10} \\\\ x&=25^{\circ} \end{aligned}$

Teaching tips for quadrilateral angles

Encourage students to classify different types of quadrilaterals (square, rectangle, parallelogram, trapezoid, rhombus) and compare their angle properties.

Provide worksheets that involve finding unknown angles in quadrilaterals and applying properties of specific quadrilateral types.

Students should be familiar with different types of quadrilaterals from elementary school ( $3$ rd grade, $4$ th grade, $5$ th grade) but if needed, provide a quick intro to each type including their properties.

Easy mistakes to make

Mistaking the sum of quadrilateral angles with the angles in a triangle
The angle sum is remembered incorrectly as $180^{\circ},$ rather than $360^{\circ}.$ The sum of angles in a triangle is equal to $180^{\circ}.$

Joining all the diagonals
When recalling the angle sum in a quadrilateral, students join all the diagonals together, creating $4$ triangles. This makes their angle sum $720^{\circ}$ which is also incorrect.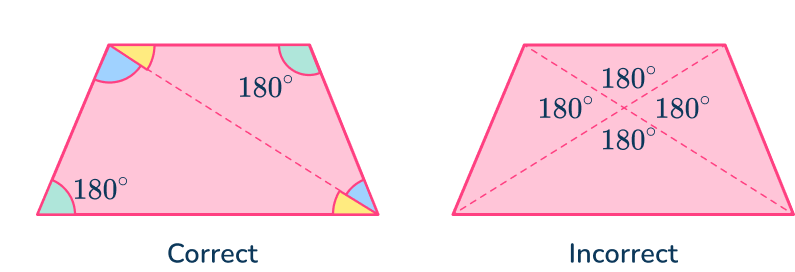

Using an incorrect angle fact
A common mistake is to use the incorrect angle fact or make an incorrect assumption to overcome a problem.
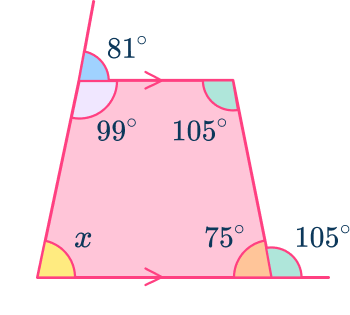
For example, here the trapezoid is assumed to be symmetrical (an isosceles trapezoid) so the interior angles are easy to deduce. This is not always true and so you should use co-interior angles instead.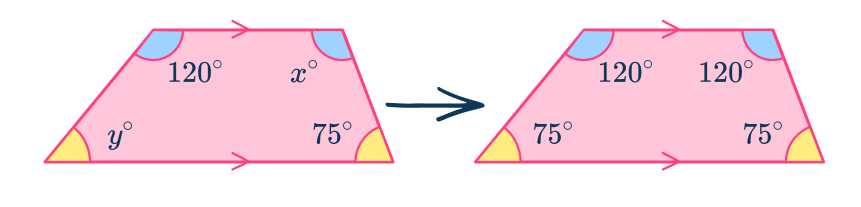

Here, the angle $x$ should be equal to $105^{\circ}$ and y should be equal to $60^{\circ}$ due to co-interior angles in parallel lines.

Interior and exterior angles of polygons
Interior angles of a polygon
Sum of exterior angles of a polygon
Angles of a hexagon

Practice quadrilateral angles questions

84^{\circ}

96^{\circ}

6^{\circ}

168^{\circ}

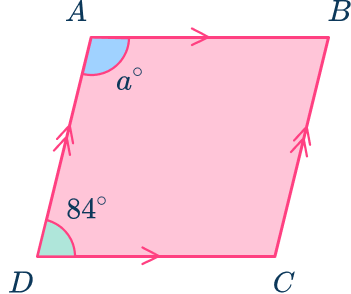
Diagonally opposite angles in a rhombus are equal

Co-interior angles add to equal $180^{\circ}.$

180-84=96^{\circ}

89^{\circ}

72^{\circ}

199^{\circ}

91^{\circ}

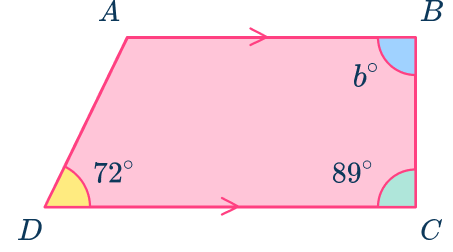
Co-interior angles add to equal $180^{\circ}.$

180-89=91^{\circ}

100^{\circ}

50^{\circ}

40^{\circ}

200^{\circ}

The sum of co-interior angles is $180^{\circ}$ so

\begin{aligned}5x+4x&=180 \\\\ 9x&=180 \\\\ x&=20 \end{aligned}

BCD=5x=100^{\circ}

155^{\circ}

279^{\circ}

223^{\circ}

137^{\circ}

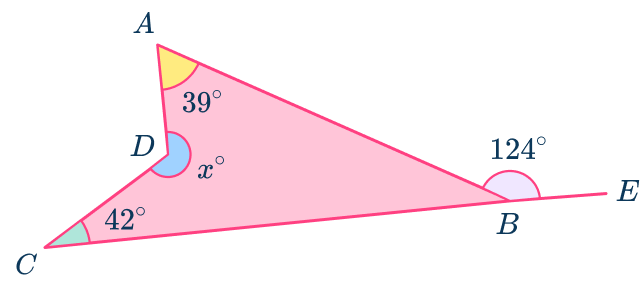
Angles on a straight line add to equal $180^{\circ}.$

180-124=56^{\circ}

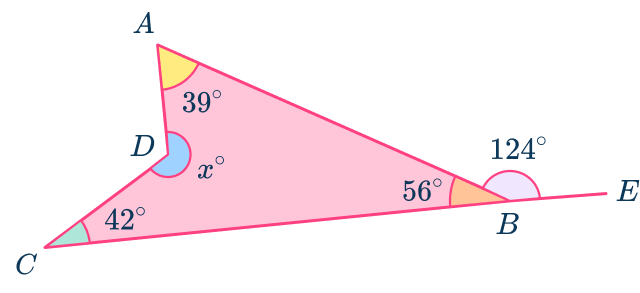
Quadrilateral angles 36 US

Angles of a quadrilateral add up to $360^{\circ}.$

\begin{aligned}39+56+42+x&=360 \\\\ x+130&=360 \\\\ x&=223^{\circ} \end{aligned}

125^{\circ}

55^{\circ}

155^{\circ}

175^{\circ}

$ADC=BCD$ so

\begin{aligned}2x+25&=3x-25 \\\\ 2x+50&=3x \\\\ x&=50^{\circ} \end{aligned}

\begin{aligned}y&=180-(3\times{50-25}) \\\\ &=180-125 \\\\ &=55^{\circ} \end{aligned}

84^{\circ}

6^{\circ}

168^{\circ}

100^{\circ}

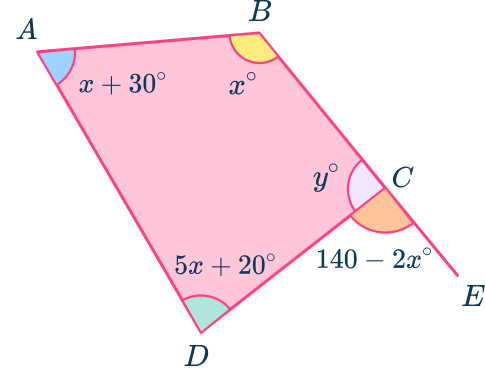
Angles on a straight line add to equal $180^{\circ}.$

y=180-(140-2x)=2x+40

x+30+x+5x+20+2x+40=9x+90

Quadrilateral angles add to equal $360^{\circ}.$

9x+90=360^{\circ}

\begin{aligned}9x+90-90&=360-90 \\\\ 9x&=270 \\\\ x&=30^{\circ} \end{aligned}

As $x=30^{\circ},~y=2x+40=2\times{30+40}=100^{\circ}.$

Quadrilateral angles FAQs

What is a quadrilateral?

A quadrilateral is a closed figure/polygon with four sides and four vertices (corners). The sum of its interior angles is always $360$ degrees.

Quadrilaterals can be classified into various types based on their side lengths, angles, and symmetry, including squares, rectangles, parallelograms, rhombuses, trapezoids, and kites. Each type of quadrilateral has its own set of properties and characteristics.

How are quadrilateral angles different from the interior angles of a polygon?

Quadrilateral angles are different from angles of other polygons primarily in their sum.

The sum of the interior angles of a quadrilateral is always $360$ degrees, while for other polygons, the sum is calculated using the formula $(𝑛−2) \times 180$ degrees, where $𝑛$ is the number of sides.

For example, a triangle’s angles add up to $180$ degrees, and a pentagon’s angles add up to $540$ degrees.

Where are the adjacent angles in a quadrilateral?

In a quadrilateral, adjacent angles are pairs of angles that share a common side (adjacent side). Since a quadrilateral has four sides and four angles, each angle has two adjacent angles.

Is a protractor needed for measuring quadrilateral angles?

While some angles in special types of quadrilaterals (like rectangles or squares) can be inferred without measurement due to their known properties (e.g., all angles in a rectangle are $90$ degrees), a protractor is necessary for precise measurement, especially in irregular quadrilaterals where the angles are not equal or known in advance.

The next lessons are

Congruence and similarity
Transformations
Mathematical proof

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.