High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Right triangle Area of a square Area of a rectangleArea of a right triangle
Here you will learn how to find the area of a right triangle, including what formula to use and why it works.
Students will first learn about the area of right triangles as part of geometry in 6th grade.
What is the area of a right triangle?
The area of a right triangle is the amount of the space inside a right triangle.
A right triangle is a type of triangle that has a right angle. The right angle is always opposite of the longest side of the triangle.

In order to find the area of a right triangle, start with the area of a rectangle.
The area of the rectangle is calculated by multiplying the \text { base } \times \text { height}.

Within a rectangle, there are two congruent right triangles. They can be shown by connecting two opposite vertices.

The area of the rectangle is the same as two congruent right triangles. This means the area of each right triangle is exactly half the area of the rectangle.
The general formula to find the area of any triangle is:
\text { Area of a triangle } = \cfrac{\text { base } \times \text { height }}{2}
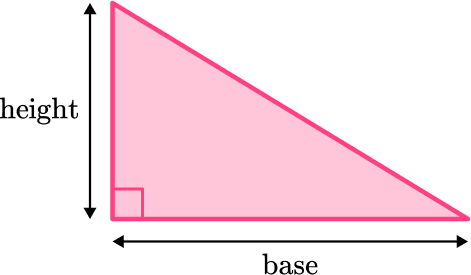
This can also be written as the following formula:
A=\cfrac{1}{2} \, b h
where b is the base length and h is the height of the triangle.
The space inside of shapes is measured in square units, so the final answer must be given in \text {units}^2 . For example, \mathrm{cm}^2, \mathrm{~m}^2, \mathrm{~mm}^2 .
For example,
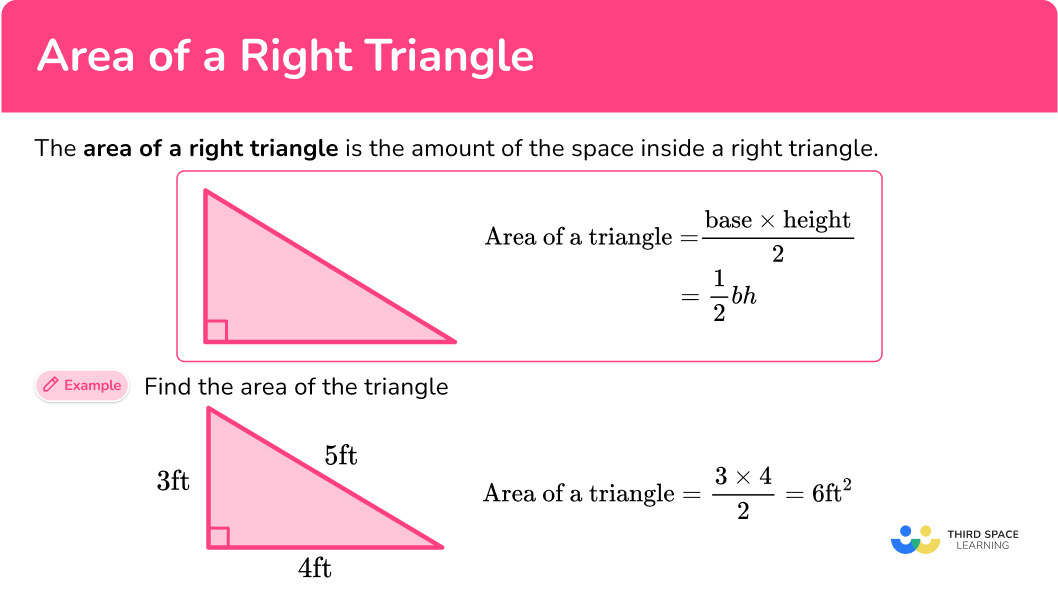
What is the area of the right triangle?

A=\cfrac{1}{2} \, b h
The base is 4 and the height is 3 .
A few things to note:
- The height of a triangle is always a perpendicular line that starts at a vertex and intersects with the opposite side of the triangle at a 90 degree angle.
- The other side lengths of the triangle may be given, but they are extra information.
\begin{aligned} & A=\cfrac{1}{2} \times 4 \times 3 \\\\ & A=2 \times 3 \\\\ & A=6 \end{aligned}
The area of the right triangle is 6 ft^2 .
What is area of a right triangle?
![[FREE] Area Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
[FREE] Area Check for Understanding Quiz (Grade 4 to 6)
![[FREE] Area Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 to 6 students’ understanding of area. 15+ questions with answers covering a range of 4th, 5th and 6th grade area topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Area Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
[FREE] Area Check for Understanding Quiz (Grade 4 to 6)
![[FREE] Area Check for Understanding Quiz (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Area-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 to 6 students’ understanding of area. 15+ questions with answers covering a range of 4th, 5th and 6th grade area topics to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this relate to 6th grade math?
- Grade 6 – Geometry (6.G.A.1)
Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems.
How to find the area of a right triangle
In order to find the area of a right triangle:
- Identify the base and perpendicular height of the triangle.
- Write the area formula.
- Substitute known values into the area formula.
- Solve the equation.
- Write the answer, including the units.
Area of right triangle examples
Example 1: given base length and height
Find the area of the triangle below:

- Identify the base and perpendicular height of the triangle.
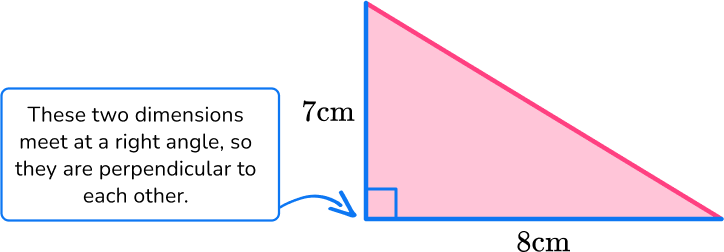
b = 8 \, cm
h = 7 \, cm
2Write the area formula.
A=\cfrac{1}{2} \, b h
3Substitute known values into the area formula.
\begin{aligned} A &=\cfrac{1}{2} \, b h \\\\ &=\cfrac{1}{2} \, (8)(7) \end{aligned}
4Solve the equation.
\begin{aligned} A &=\cfrac{1}{2} \, b h \\\\ &=\cfrac{1}{2} \, (8)(7)\\\\ &=28 \end{aligned}
5Write the answer, including the units.
A=28 \mathrm{~cm}^2
Remember: Your final answer must be in units squared.
Example 2: given base length and height
Find the area of the triangle below:

Identify the base and perpendicular height of the triangle.
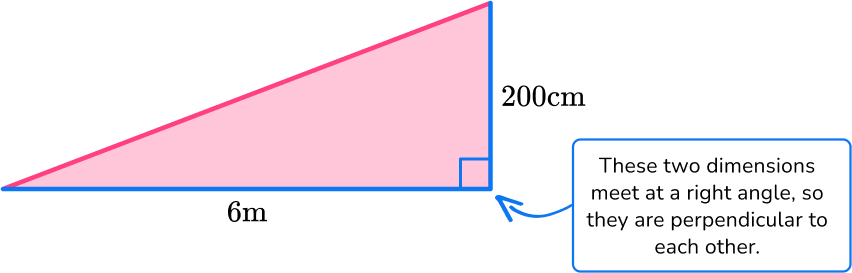
b = 6 \, m
h = 200 \, cm
Notice, there are 2 different units here. You must convert them to a common unit:
200 \, cm = 2 \, m
b = 6 \, m
h = 2 \, m
Write the area formula.
A=\cfrac{1}{2} \, b h
Substitute known values into the area formula.
\begin{aligned} A &=\cfrac{1}{2} \, b h \\\\ &=\cfrac{1}{2} \, (6)(2) \end{aligned}
Solve the equation.
\begin{aligned} A &=\cfrac{1}{2} \, b h \\\\ &=\cfrac{1}{2} \, (6)(2)\\\\ &=6\end{aligned}
Write the answer, including the units.
A=6 \, m^2
Example 3: given base length and height and hypotenuse
Find the area of triangle BAC below:
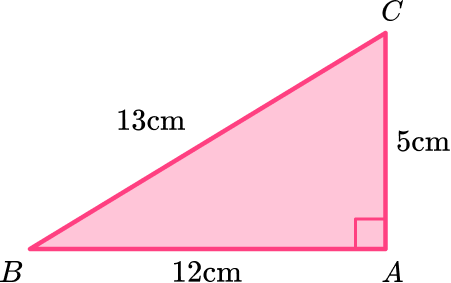
Identify the base and perpendicular height of the triangle.
b = 12 \, cm
h = 5 \, cm
Note: The 13 \, cm is not needed to solve. It is extra information.
Write the area formula.
A=\cfrac{1}{2} \, b h
Substitute known values into the area formula.
\begin{aligned} A &=\cfrac{1}{2} \, b h \\\\ &=\cfrac{1}{2} \, (12)(5) \end{aligned}
Solve the equation.
\begin{aligned} A &=\cfrac{1}{2} \, b h \\\\ &=\cfrac{1}{2} \, (5)(12) \\\\ &=30 \end{aligned}
Write the answer, including the units.
A=30 \, cm^2
Example 4: area of the isosceles right triangle – fraction
Find the area of triangle below:
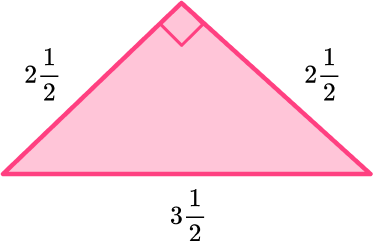
Identify the base and perpendicular height of the triangle.
Rotating the triangle makes it easier to identify the base and height.
\begin{aligned} & \mathrm{b}=2 \, \cfrac{1}{2} \\\\ & \mathrm{h}=2 \, \cfrac{1}{2} \end{aligned}
Write the area formula.
A=\cfrac{1}{2} \, b h
Substitute known values into the area formula.
\begin{aligned} A & = \cfrac{1}{2} \, b h \\\\ & = \cfrac{1}{2} \, \left(2 \, \cfrac{1}{2} \, \right) \left(2 \, \cfrac{1}{2} \, \right) \end{aligned}
Solve the equation.
\begin{aligned} A & =\cfrac{1}{2} \, b h \\\\ & =\cfrac{1}{2} \, \left(2 \, \cfrac{1}{2} \, \right) \left(2 \, \cfrac{1}{2} \, \right) \\\\ & =3 \, \cfrac{1}{8} \end{aligned}
Write the answer, including the units.
A=3 \, \cfrac{1}{8} \text { units}^2
Note, when no units are given the answer can be labeled with the general term \text {units}^2.
Example 5: compound shape
Below is the floor plan for a new deck that needs to be painted. One can of paint costs \$12 and covers an area of 2.5 \, m^2. How much would it cost to paint the entire deck?
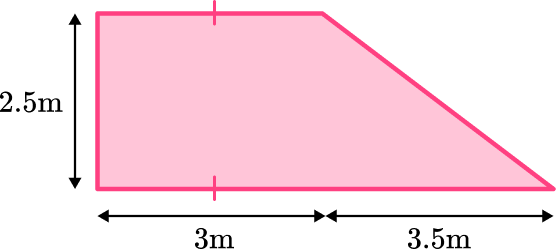
Identify the base and perpendicular height of the triangle.
Split the plan into 2 shapes; a rectangle and a right triangle.
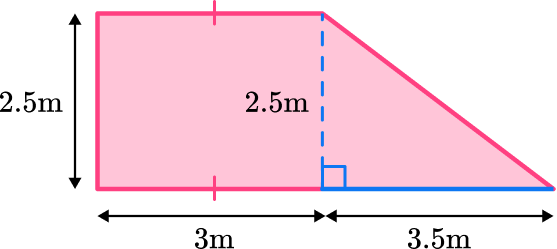
For the triangle:
b = 3.5 \, m
h = 2.5 \, m
Write the area formula.
A=\cfrac{1}{2} \, b h
Substitute known values into the area formula.
\begin{aligned} A &=\cfrac{1}{2} \, b h \\\\ &=\cfrac{1}{2} \, (3.5)(2.5) \end{aligned}
Solve the equation.
\begin{aligned} A &=\cfrac{1}{2} \, b h \\\\ &=\cfrac{1}{2} \, (2.5)(3.5)\\\\ &=4.375 \end{aligned}
Now you must find the area of the rectangle.
\begin{aligned}
\text { Area of a rectangle }&=l \times w \\\\
&=2.5 \times 3 \\\\
&=7.5 \end{aligned}
Write the answer, including the units.
Total Area = 4.375+7.5=11.875 \, m^2
Now divide 11.875 by 2.5 since one can of paint only covers an area of 2.5 \, m^2 .
11.875 \div 2.5=4.75
Since you can’t buy 0.75 paint cans and 4.75 is not quite enough, you have to buy 5 cans of paint.
Multiply to find the cost: 5 \text { cans of paint } \times \$ 12=\$ 60 .
The total cost to paint the deck is \$60 .
Example 6: calculating base length
Triangle XYZ is a right triangle with an area of 15 \, cm^2 . The height of the triangle is 5 \, cm . Find the base length of the triangle.
Identify the base and perpendicular height of the triangle.
\begin{aligned} A &=15 \mathrm{~cm}^2 \\\\ b &= \, ? \\\\ h &=5 \mathrm{~cm} \end{aligned}
Write the area formula.
A=\cfrac{1}{2} \, b h
Substitute known values into the area formula.
\begin{aligned} & A=\cfrac{1}{2} \, b h \\\\ & 15=\cfrac{1}{2} \, \times b \times 5 \\\\ & 15=\cfrac{1}{2} \, \times 5 \times b \\\\ & 15=2.5 \times b \end{aligned}
Solve the equation.
15=2.5 \times b
To solve, find what times 2.5 is equal to 15 . Since 2.5 \times 6=15 , the base is 6 .
Write the answer, including the units.
b=6 \mathrm{~cm}
The units are not squared, because the base is the length of the bottom of the triangle (one-dimensional), not the square units within the triangle (two-dimensional).
Teaching tips for the area of a right triangle
- Start by connecting the area of right triangles to the area of rectangles. One easy way to do this is to have students take a rectangular piece of paper and cut it diagonally – forming 2 right triangles. Then ask students to make conjectures about the area of the triangles – including discussing their ideas with other students and supporting any claims with evidence and mathematical reasoning.
- Choose worksheets that include a variety of right triangles, in all orientations. This includes right triangles with the right angle on the right side, left side or at the top of a triangle (with the hypotenuse appearing horizontally).
This forces students to think flexibly about the position of the triangle and requires them to think about the perpendicular relationship between the base and the height, instead of just assuming that the two measurements given are what is needed to calculate the area.
Easy mistakes to make
- Confusing which measures represent the base and the height
A question may give more than two measurements on a triangle, some of which will not be needed. Carefully identify the perpendicular relationship between the base and the height to use the correct measurements.
For example,
To calculate the area here, you only need the base and height.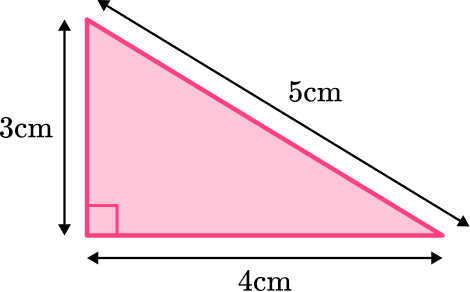
b = 4 \, cm
h = 3 \, cm
\text {Area }=\cfrac{1}{2} \, \times 4 \times 3=6 \mathrm{~cm}^2
You can ignore the length of the hypotenuse (5 \,cm) – it is not needed to solve for the area.
- Thinking the sides of a right triangle can’t be equal
While a right triangle cannot be an equilateral triangle, it can be an isosceles. The two legs that form the right angle can be equal.
For example,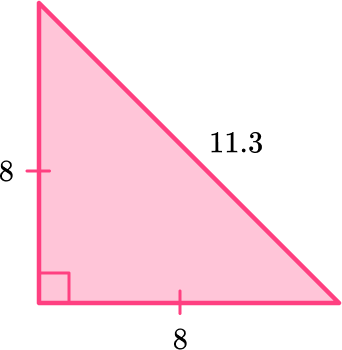
- Forgetting to record the units
It is common to forget the units for area in the final answer. When calculating area, your answer must always have square units.
Practice area of right triangles questions
1. What is the area of this triangle?





The area of a triangle is calculated with the formula: A=\cfrac{1}{2} \, b h .
Rotating the triangle makes it easier to identify the base and height.
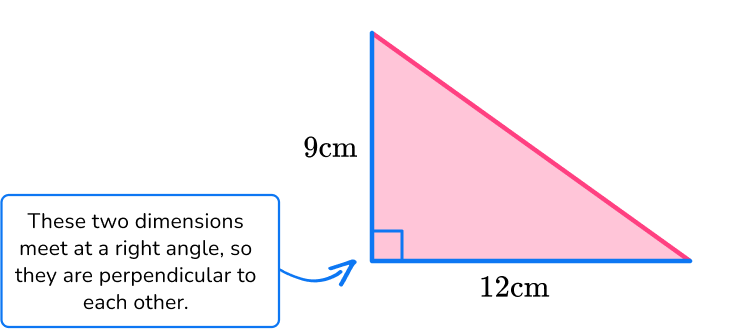
For this triangle:
b = 12 \, cm
h = 9 \, m
Substitute the values into the formula.
\begin{aligned} A & =\cfrac{1}{2} \, b h \\\\ & =\cfrac{1}{2} \, (12)(9) \\\\ & =54 \mathrm{~cm}^2 \end{aligned}
2. Find the area of the triangle below:
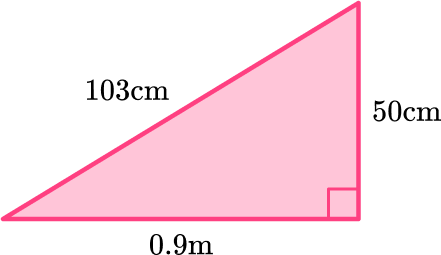




The area of a triangle is calculated with the formula: A=\cfrac{1}{2} \, b h.
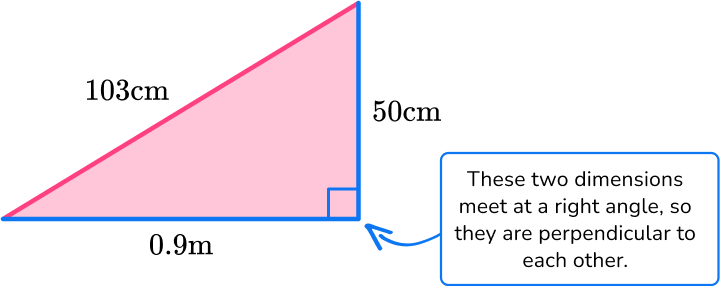
For this triangle:
b = 0.9 \, m
h = 50 \, cm
Since the measurements are in different units (m and cm), they need to be converted to the same unit:
0.9 \, m = 90 \, cm.
b = 90 \, cm
h = 50 \, cm
Note: 103 \, cm is not needed to solve. It is extra information.
Substitute the values into the formula.
\begin{aligned} A & =\cfrac{1}{2} \, b h \\\\ & =\cfrac{1}{2} \, (90)(50) \\\\ & =2,250 \mathrm{~cm}^2 \end{aligned}
3. Shown below is a compound shaped meerkat enclosure. Each meerkat needs a minimum of 9 \, m^2 to roam around. What is the maximum number of meerkats that can fit into this cage?

2 meerkats

3 meerkats

24 meerkats

25 meerkats

The shape can be split into a rectangle and a triangle. The opposite sides of the rectangle are congruent.
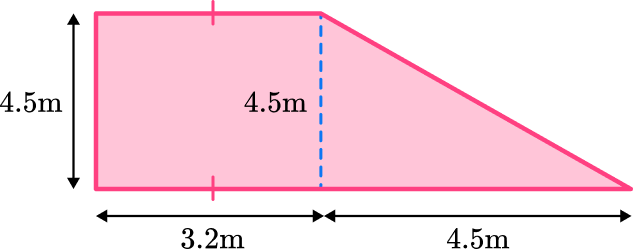
The area of the rectangle is 4.5 \times 3.2 = 14.4 \, m^{2}
The area of the triangle is \cfrac{1}{2} \, \times 4.5 \times 4.5 = 10.125 \, m^{2}
This means the total area is 14.4+ 10.125 = 24.525 \, m^{2}
Now to calculate how many meerkats will fit into the enclosure, take 24.525 \, m^2 and divide it by 9 \, m^2, because each meerkat needs that much space to roam.
24.525 \div 9 = 2.725
The quotient has 2 wholes and 725 thousandths.
There cannot be part of a meerkat and 2.725 is not enough for 3 meerkats.
So, 2 meerkats will fit in the enclosure.
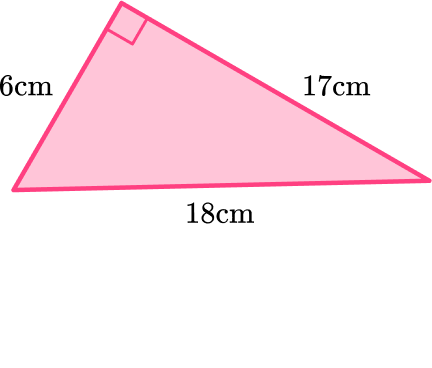
4. Find the area of the triangle below:




The area of a triangle is calculated with the formula:
A=\cfrac{1}{2} \, b h .
Rotating the triangle makes it easier to identify the base and height.
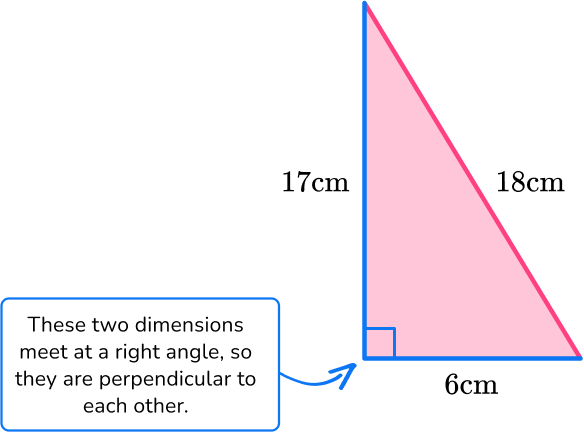
For this triangle:
b = 6 \, cm
h = 17 \, cm
Substitute the values into the formula.
\begin{aligned} A & =\cfrac{1}{2} \, b h \\\\ & =\cfrac{1}{2} \, (6)(17) \\\\ & =51 \mathrm{~cm}^2 \end{aligned}
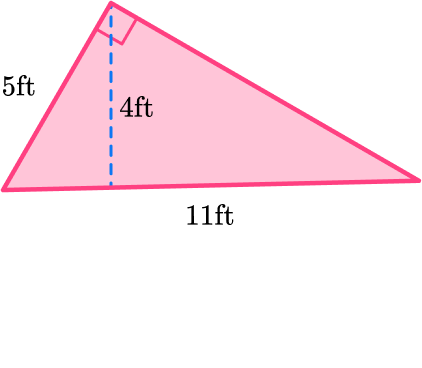
5. Find the area of the triangle below:




The area of a triangle is calculated with the formula:
A=\cfrac{1}{2} \, b h .
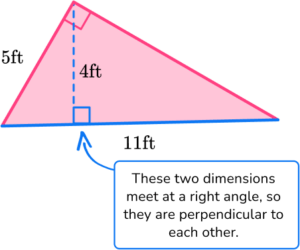
For this triangle:
b = 11 \, ft
h = 4 \, ft
Substitute the values into the formula.
\begin{aligned} A & =\cfrac{1}{2} \, b h \\\\ & =\cfrac{1}{2} \, (11)(4) \\\\ & =22 \, f t^2 \end{aligned}
6. Triangle PQR is a right triangle with an area of 40{cm}^2 . The base length of the triangle is 0.1 \, m . Find the height of the triangle.




The area of a triangle is calculated with the formula:
A=\cfrac{1}{2} \, b h .
\begin{aligned} & A=40 \mathrm{~cm}^2 \\\\ & b=0.1 \mathrm{~m} \\\\ & h= \, ? \end{aligned}
Since the measurements are in different units ( m and cm ), they need to be converted to the same unit:
0.1 \, m = 10 \, cm .
\begin{aligned} & A=40 \mathrm{~cm}^2 \\\\ & b=10 \mathrm{~cm} \end{aligned}
\begin{aligned} & A=\cfrac{1}{2} \, b h \\\\ & 40=\cfrac{1}{2} \, \times 10 \times h \\\\ & 40=5 \times h \end{aligned}
To solve, find what times 5 is equal to 40 .
Since 5 \times 8=40 , the base is 8 \, cm .
Area of a right triangle FAQs
The perimeter is the distance around the right triangle. To calculate perimeter, add the lengths of the three sides together.
The pythagorean theorem is shown by the formula a^2+b^2=c^2 , where c is the hypotenuse of a right triangle (longest side of a right triangle) and a and b are adjacent sides of the triangle.
The theorem explains a relationship between the sides that make up right triangles and can be used to find a missing third side of a right triangle, if the two other side lengths are given.
The next lessons are:
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!