Sector of a Circle - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Circle math

Area of a circle Circumference of a circle Arc of a circle

Trigonometry

Law of sines Law of cosines Rounding Square roots

Math resources Geometry

Angles of a circle

Sector of a circle

Here you will learn about sectors of a circle, including how to find the area of a sector, the perimeter of a sector, and solve problems involving sectors of circles.

Students will first learn about the sector of a circle as part of geometry in high school.

What is a sector of a circle?

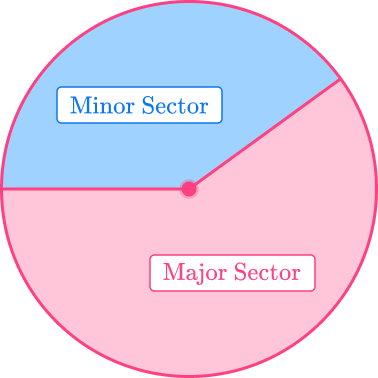
A sector of a circle is formed when a circle is divided using two radii.

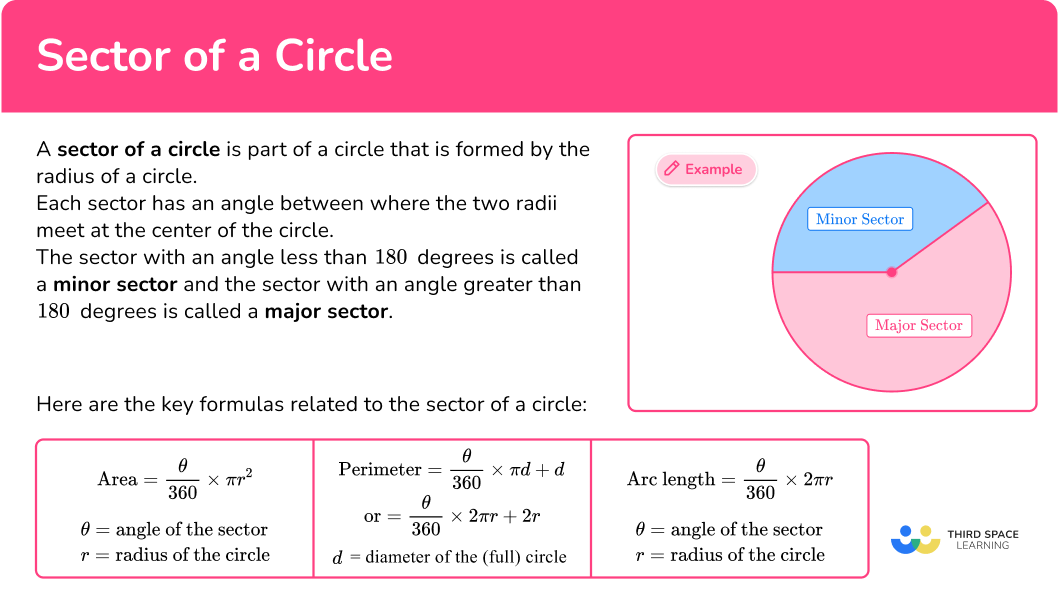
Each sector has an angle between the two radii. The sector with an angle less than $180$ degrees is called a minor sector and the sector with an angle greater than $180$ degrees is called a major sector. If the central angle formed equals $180$ degrees, the two sectors would be semicircles.

For example,

You will need to know how to solve problems involving the area of the sector of a circle and the perimeter of a sector of a circle. You may be asked to give exact answers in terms of $\pi$ or using decimals.

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

DOWNLOAD FREE

[FREE] Common Core Practice Tests (Grades 3 to 6)

DOWNLOAD FREE

Area of a sector

The area of a sector is the space inside the section of the circle created by two radii and an arc. It is a fraction of the area of the full circle.

The formula to find the area of a sector is,

$\text{Area of a sector}=\cfrac{\theta}{360}\times\pi{r^2}$

$\theta =$ angle of the sector

$r =$ radius of the circle

Perimeter of a sector

The perimeter of a sector is the distance around a sector.

You can calculate the perimeter of a sector by adding together the lengths of the two radii and the arc length of the sector.

To find the length of an arc of a sector you need to use the formula,

$\text{Arc length}=\cfrac{\theta}{360}\times\pi\times{d}$

$\theta = \text{ Angle of the sector}$

$r =$ Radius of the circle

$\text{Arc length}=\cfrac{\theta}{360}\times{2\pi{r}}$

$\theta =$ Angle of the sector

$r =$ Radius of the circle

The total perimeter of a sector formula would be,

\text{Perimeter of a sector } = \text{ Arc length } + \text{ radius } + \text{ radius}

\begin{aligned} &=\cfrac{\theta}{360}\times\pi{d}+d \\\\ &\text{or} \\\\ &=\cfrac{\theta}{360}\times{2\pi{r}} +2r \end{aligned}

What is a sector of a circle?

Common Core State Standards

How does this relate to high school math?

High School – Geometry – Circles (HS.G.C.B.5)
Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector.

How to calculate the area of a sector of a circle

In order to calculate the area of a sector:

Find the length of the radius.
Find the size of the angle creating the sector.
Substitute the values you know into the formula for the area of a sector.
Calculate the answer.

Area of a sector of a circle examples

Example 1: finding the area of a sector given the radius and angle

Calculate the area of the sector shown below. Give your answer to the nearest tenth.

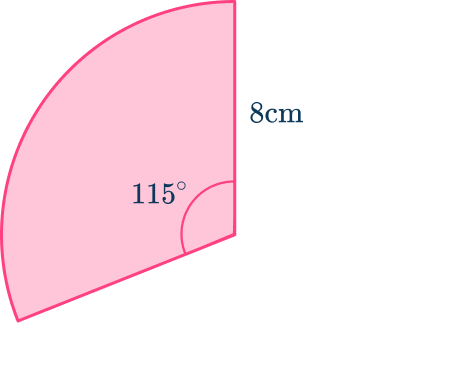
Find the length of the radius.

Radius $r=8\mathrm{~cm}$

2Find the size of the angle creating the sector.

\theta=115^{\circ}

3Substitute the values you know into the formula for the area of a sector.

\begin{aligned}\text{Area of a sector}&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{115}{360}\times\pi\times8^{2} \\\\ &=\cfrac{184}{9}\pi \end{aligned}

4Calculate the answer.

The question asked you to round your answer to the nearest tenth.

\begin{aligned}\text{Area of a sector}&=\cfrac{184}{9}\pi\mathrm{~cm^{2}} \\\\ &=64.228…\mathrm{~cm^2} \\\\ &=64.2\mathrm{~cm^{2}}\text{ (1dp)} \end{aligned}

Example 2: finding the area of a sector not given the angle

Calculate the area of the sector shown below. Give your answer to the nearest tenth.

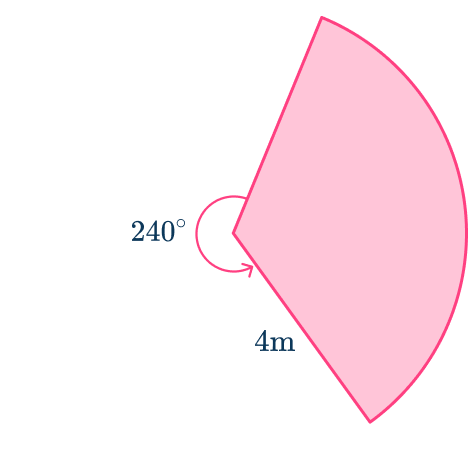
Find the length of the radius.

Radius $r=4\mathrm{~m}$

Find the size of the angle creating the sector.

The angle creating the sector is the angle included between the two radii. To find it in this case, you need to use the angle fact: angles around a point add to $360^{\circ}.$

$360-240=120^{\circ}$

The angle creating the sector is $120^{\circ}.$

Substitute the values you know into the formula for the area of a sector.

\begin{aligned}\text{Area of a sector}&=\cfrac{\theta}{360}\times\pi\times{r^2} \\\\ &=\cfrac{120}{360}\times\pi\times{4^2} \end{aligned}

Calculate the answer.

\begin{aligned}&=16.75516083 \\\\ &=16.8\mathrm{~m}^{2} \end{aligned}

Example 3: finding the area of a sector not given the radius or angle

Below is a sector of a circle. The diameter of the circle is $12\mathrm{~cm}.$ Calculate the area of the sector. Give your answer to the nearest tenth.

Find the length of the radius.

Diameter $d=12\mathrm{~cm}$

The radius is half of the diameter, so the radius $r=6\mathrm{~cm}.$

Find the size of the angle creating the sector.

The angle creating the sector is the angle included between the two radii. To find it in this case, you need to use the angle fact: angles around a point add to $360^{\circ}.$

$360-205=155^{\circ}$

The angle creating the sector is $155^{\circ}.$

Substitute the values you know into the formula for the area of a sector.

\begin{aligned}\text{Area of a sector}&=\cfrac{\theta}{360}\times\pi\times{r^2} \\\\ &=\cfrac{155}{360}\times\pi\times{6^2} \end{aligned}

Calculate the answer.

\begin{aligned}&=48.69468613 \\\\ &=48.7\mathrm{~cm}^{2} \end{aligned}

How to calculate the perimeter of a sector

In order to calculate the perimeter of a sector:

Find the length of the radius.
Find the size of the angle creating the sector.
Substitute the values you know into the formula for the arc length.
Add together the arc length and the two radii.

Perimeter of a sector examples

Example 4: finding the perimeter of a sector given the angle

Calculate the perimeter of the sector shown below. Give your answer to the nearest tenth.

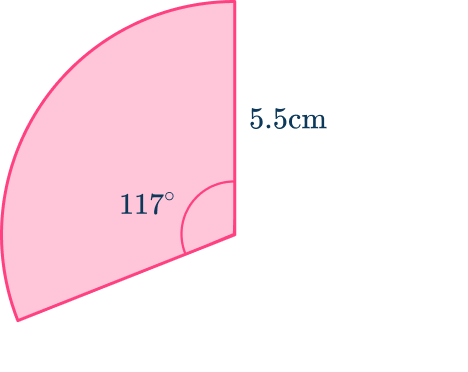
Find the length of the radius.

Radius $r=5.5\mathrm{~cm}$

Find the size of the angle creating the sector.

Angle $\theta=117^{\circ}$

Find the arc length of the sector.

\begin{aligned}\text{Arc length}&=\cfrac{\theta}{360}\times{2}\times\pi\times{r} \\\\ &=\cfrac{117}{360}\times{2}\times\pi\times{5.5} \\\\ &=\cfrac{143}{40}\pi \end{aligned}

Add together the arc length and the two radii.

Arc length: $\cfrac{143}{40}\pi\mathrm{~cm}$

Radius: $5.5\mathrm{~cm}$

\begin{aligned}\text{Perimeter}&=\cfrac{143}{40}\pi+5.5+5.5 \\\\ &=\cfrac{143}{40}\pi+11 \\\\ &=22.2311… \\\\ &=22.2\mathrm{~cm} \end{aligned}

Example 5: finding the perimeter of a sector not given the angle

Calculate the perimeter of the sector shown below. Give your answer to the nearest tenth.

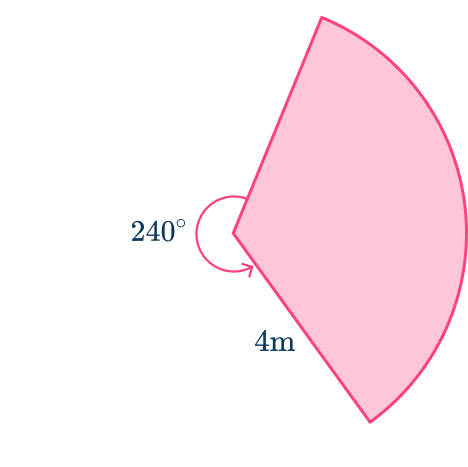
Find the length of the radius.

Radius $r=4\mathrm{~m}$

Find the size of the angle creating the sector.

The angle creating the sector is the angle included between the two radii. To find it in this case, you need to use the angle fact: angles around a point add to $360^{\circ}.$

$360-240=120^{\circ}$

The angle creating the sector is $120^{\circ}.$

Substitute the values you know into the formula for the arc length.

\begin{aligned}\text{Arc length}&=\cfrac{\theta}{360}\times{2}\times\pi\times{r} \\\\ &=\cfrac{120}{360}\times{2}\times\pi\times{4} \\\\ &=8.37758041\mathrm{~cm} \end{aligned}

Add together the arc length and the two radii.

\begin{aligned}&8.377580+4+4 \\\\ &=16.37758041 \\\\ &=16.4\mathrm{~cm} \end{aligned}

Example 6: finding the perimeter of a sector not given the radius or angle

Below is a sector of a circle. The diameter of the circle is $12\mathrm{~cm}.$ Calculate the perimeter of the sector. Give your answer to the nearest tenth.

Find the length of the radius.

Diameter $d=12\mathrm{~cm}$

The radius is half of the diameter, so, the radius $r=6\mathrm{~cm}.$

You can use the radius or diameter as long as you use the correct formula for each.

Find the size of the angle creating the sector.

The angle creating the sector is the angle included between the two radii. To find it in this case, you need to use the angle fact: angles around a point add to $360^{\circ}.$

$360-205=155^{\circ}$

The angle creating the sector is $155^{\circ}.$

Substitute the values you know into the formula for the arc length.

\begin{aligned}\text{Arc length}&=\cfrac{\theta}{360}\times{2}\times\pi\times{r} \\\\ &=\cfrac{155}{360}\times{2}\times\pi\times{6} \\\\ &=16.23156204\mathrm{~cm} \end{aligned}

Add together the arc length and the two radii.

\begin{aligned}&16.23156204+6+6 \\\\ &=28.23156204 \\\\ &=28.2\mathrm{~cm} \end{aligned}

Teaching tips for sector of a circle

Have students work in groups to complete worksheets involving sectors, encouraging peer teaching and discussion.

Provide practice questions involving real-life objects like pizza slices, pie charts, and sections of a Ferris wheel.

Create study materials with key terms like “sector,” “central angle,” “radius,” “arc,” and “circle.”

Easy mistakes to make

Confusing the segment/sector
A segment of a circle is made from a chord while a sector will have lines (radii) coming from the origin. Sectors are a part of a circle – it can be helpful to think of a sector as a pizza slice.

Finding the area of the whole circle not the area of the sector
Remember to find the fraction of the circle that makes the sector not just the area of the whole circle. Use $\cfrac{\theta}{360}\times\pi{r^2}$ not $\pi{r^2}$ to find the area of a sector.

Finding the length of the arc not the perimeter of the sector
You must remember that the perimeter of the sector is the combined length of the arc and the two radii.

Using incorrect units
Remember the perimeter is a length and therefore the units will not be squared or cubed. Square units are for area and cubed units are for volume.

Incorrect angle unit set on calculator
All angles are measured in degrees. Make sure that your calculator has a small $‘d’$ for degrees at the top of the screen rather than an $‘r’$ for radians.

Angles of a circle
Segment of a circle
Area of a segment of a circle
Arc length formula
Perimeter of a sector
Area of a sector

Practice sector of a circle questions

16\pi\mathrm{~cm}^2

8\pi\mathrm{~cm}^2

\cfrac{8}{3} \, \pi\mathrm{~cm}^2

8.4\pi\mathrm{~cm}^2

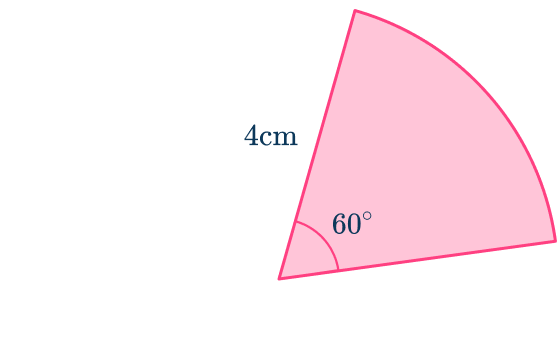
Substitute the values you know into the formula for the area of a sector.

\begin{aligned}&\text{Area of a sector}=\cfrac{\theta}{360}\times\pi\times{r^2} \\\\ &=\cfrac{60}{360}\times\pi\times{4^2} \\\\ &=\cfrac{8}{3} \, \pi\mathrm{~cm}^{2} \end{aligned}

45^{\circ}

30^{\circ}

60^{\circ}

90^{\circ}

Substituting the known values into the formula for the area of a sector,

\cfrac{\theta}{360}\times\pi\times{12^2}=18\pi

Solving for angle $\theta,$

\theta=45^{\circ}

12\mathrm{~cm}

6\mathrm{~cm}

9\mathrm{~cm}

36\mathrm{~cm}

Substituting the known values into the formula for the area of a sector,

\cfrac{210}{360}\times\pi\times{r^2}=21\pi

Solving for radius $r,$

\begin{aligned}r^{2}&=36 \\\\\ r&=\sqrt{36}=6\mathrm{~cm} \end{aligned}

8.19\mathrm{~cm}

16.38\mathrm{~cm}

10.09\mathrm{~cm}

12.19\mathrm{~cm}

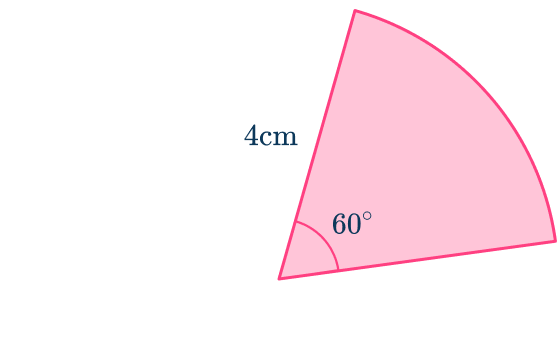
Substituting the known values into the formula for the arc length,

\begin{aligned}\text{Arc length}&=\cfrac{\theta}{360}\times{2}\times\pi\times{r} \\\\ &=\cfrac{60}{360}\times{2}\times\pi\times{4} \\\\ &=4.188790205\mathrm{~cm} \end{aligned}

Adding together the arc length and the two radii,

\begin{aligned}&4.188790205+4+4 \\\\ &=12.188790205 \\\\ &=12.19\mathrm{~cm} \end{aligned}

72^{\circ}

60^{\circ}

90^{\circ}

108^{\circ}

Substituting the known values into the formula for the total perimeter,

\left(\cfrac{\theta}{360}\times{2}\times\pi\times{5}\right)+5+5=2\pi+10

Solving for $\theta,$

\theta=72^{\circ}

24\mathrm{~cm}

12\mathrm{~cm}

9\mathrm{~cm}

10\mathrm{~cm}

Substituting the known values into the formula for the total perimeter,

\left(\cfrac{24}{360}\times{2}\times\pi\times{r}\right)+2r=29.03

Rearranging to change the subject of the formula to $r,$

\begin{aligned}r\left(\cfrac{48\pi}{360}+2\right)&=29.03 \\\\ &=29.03\div\left(\cfrac{48\pi}{360}+2\right) \\\\ &=12.00142701 \\\\ &=12\mathrm{~cm} \end{aligned}

Sector of a circle FAQs

What is a sector of a circle?

A sector of a circle is a part of the circle enclosed by two radii and the arc between them, with the endpoints of the arc lying on the circumference of the circle.

What are the sector of a circle formulas?

Here are the key formulas related to the sector of a circle with all angles in degrees:

$\text{ Arc of the sector } =\cfrac{\theta}{360}\times2\pi{r}$

$\text{ Area } =\cfrac{\theta}{360}\times\pi{r^2}$

$\text{ Perimeter } =\cfrac{\theta}{360}\times2\pi{r}+2r$

Why is understanding sectors of a circle important?

Understanding sectors is important for solving problems in geometry, trigonometry, and real-world applications such as engineering, architecture, and various fields that involve circular shapes and motions.

What is the central angle of a semicircle?

The central angle of a semicircle is $180$ degrees or $\pi$ radians.

The next lessons are

Circle theorems
Prism shape
Types of data

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.