High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Circle math
Circumference of a circle Solving equations Law of sines Law of cosines Rounding Square rootArc of a circle
Here you will learn about the arc of a circle, including how to find the arc length of a circle and using the measure of an arc to solve problems.
Students will first learn about the arc of a circle as part of geometry in high school.
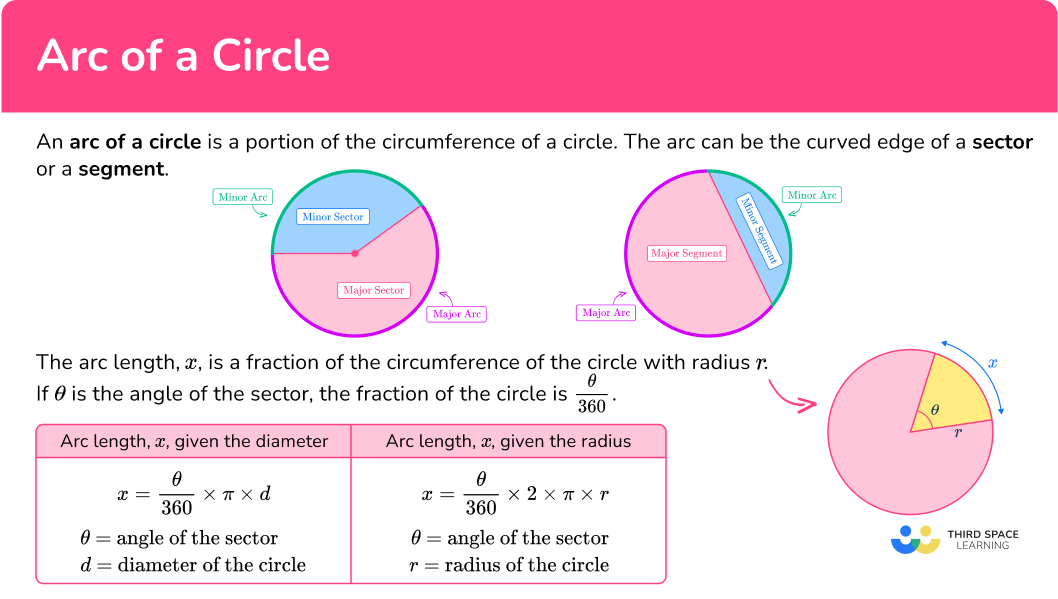
What is an arc of a circle?
An arc of a circle is a portion of the circumference of a circle. A major arc is more than half of the circumference, whilst a minor arc is less than half of the circumference.
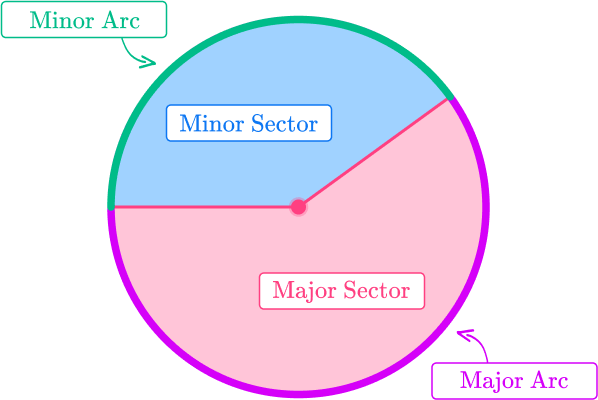
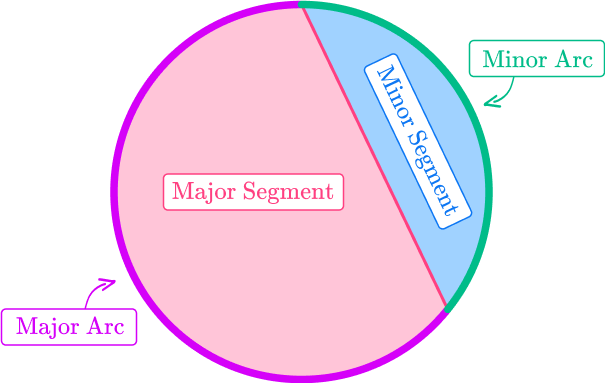
The arc of a circle is also the curved edge of a segment with the major arc around the major segment, and the minor arc around the minor segment.
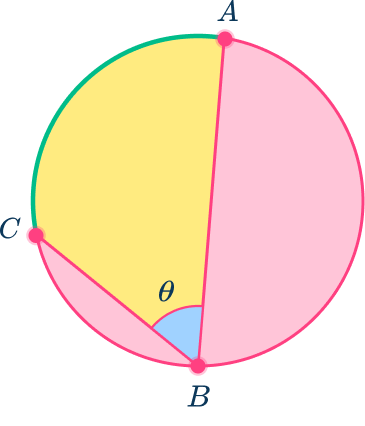
The arc of a circle can be used to define angles and lengths.
There are circle theorems that are defined using arcs of the circle.
For example, \theta is the angle subtended by arc AC.
See also: Circle Theorems
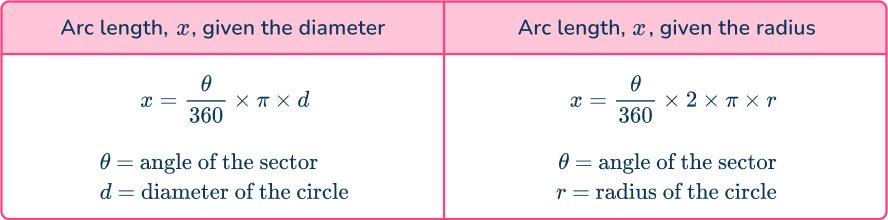
You can find the length of an arc if you know the angle of the sector.
![[FREE] Common Core Practice Tests (Grades 3 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/10/common-core-practice-tests.png)
[FREE] Common Core Practice Tests (Grades 3 to 6)
![[FREE] Common Core Practice Tests (Grades 3 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/10/common-core-practice-tests.png)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
DOWNLOAD FREE![[FREE] Common Core Practice Tests (Grades 3 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/10/common-core-practice-tests.png)
[FREE] Common Core Practice Tests (Grades 3 to 6)
![[FREE] Common Core Practice Tests (Grades 3 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/10/common-core-practice-tests.png)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
DOWNLOAD FREECalculating the arc length
The arc length, x, is a fraction of the circumference of the circle with radius r. If \theta is the angle of the sector, the fraction of the circle is \cfrac{\theta}{360}.
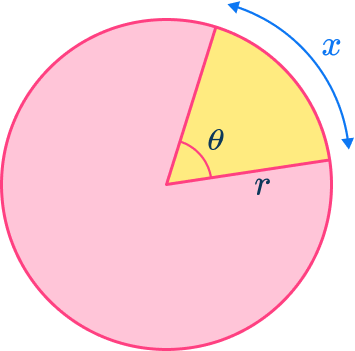
Multiplying this fraction by the circumference of the whole circle (written in terms of the diameter or the radius) gives the two arc length formulas:
What is an arc of a circle?
Common Core State Standards
How does this relate to high school math?
- High School – Geometry – Circles (HS.G.C.B.5)
Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector.
How to calculate the arc length
In order to calculate the arc length of a sector:
- Find the length of the radius or the diameter.
- Find the size of the angle creating the sector.
- Substitute the known values into the formula for the arc length and solve.
Calculating the arc length examples
Example 1: calculate the arc length given the angle
Calculate the arc length of the sector shown below.
Give your answer to the nearest tenth.

- Find the length of the radius or the diameter.
Radius: r=8\mathrm{~cm}
2Find the size of the angle creating the sector.
Angle of the sector: \theta=115^{\circ}
3Substitute the known values into the formula for the arc length and solve.
As you know the radius, you can use the formula which has ‘r’ as a variable.
\begin{aligned}x&=\cfrac{\theta}{360}\times{2}\times\pi\times{r} \\\\ &=\cfrac{115}{360}\times{2}\times\pi\times{8} \\\\ &=16.1\mathrm{~cm}\text{ (1dp)} \end{aligned}Example 2: calculate the arc length not given the angle
Calculate the arc length of the sector shown below.
Give your answer to the nearest hundredth.
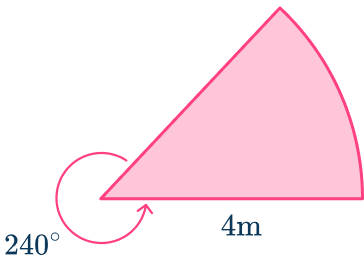
Find the length of the radius or the diameter.
Radius: r=4\mathrm{~m}
Find the size of the angle creating the sector.
As angles around a point total 360^{\circ} ,
Angle of the sector: \theta=360-240=120^{\circ}
Substitute the known values into the formula for the arc length and solve.
As you know the radius, you can use the formula which has ‘r’ as a variable.
Example 3: finding the arc length given the diameter
Below is a sector of a circle. The diameter of the circle is 12\mathrm{~cm}.
Calculate the arc length to the nearest tenth.

Find the length of the radius or the diameter.
Diameter: d=12\mathrm{~cm}
Find the size of the angle creating the sector.
As angles around a point total 360^{\circ} ,
Angle of the sector: \theta=360-205=155^{\circ}
Substitute the known values into the formula for the arc length and solve.
As you know the diameter, you can use the formula which has ‘d’ as a variable.
Example 4: word problem
The arch of a garden gate is in the shape of a circular sector, where the radius of the circle is 15\mathrm{~cm} and the central angle of the sector is 120^{\circ}. Find the length of the arc that forms the top part of the arch in terms of \pi.
Find the length of the radius or the diameter.
Radius: r=15\mathrm{~cm}.
Find the size of the angle creating the sector.
The angle of the arc: \theta=120^{\circ}.
Substitute the known values into the formula for the arc length and solve.
As you know the radius, you can use the formula which has ‘r’ as a variable.
How to solve problems given the arc length
In order to solve problems given the arc length:
- Find the known values.
- Substitute the known values into the formula for the arc length.
- Solve for the unknown value.
Example 5: work backwards
Find the angle of the sector with an arc length of 6 \mathrm{~cm} and a radius of 18\mathrm{~cm}.
Give your answer to the nearest degree.
Find the known values.
The known values are:
Arc length: x=6\mathrm{~cm}
Radius: r=18\mathrm{~cm}
Substitute the known values into the formula for the arc length.
As you know the radius, you can use the formula which has ‘r’ as a variable.
Solve for the unknown value.
First, simplify the right hand side of the equation:
6=\cfrac{\theta}{360}\times\pi\times{36}
Divide both sides by 36\text{:}
\cfrac{1}{6}=\cfrac{\theta}{360}\times\pi
Divide both sides by \pi\text{:}
\cfrac{1}{6\pi}=\cfrac{\theta}{360}
Multiply both sides by 360\text{:}
Example 6: work backwards
Find the radius of the sector with an arc length of 4.5\mathrm{~m} and an angle of 72^{\circ}.
Give your answer to the nearest centimeter.
Find the known values.
The known values are:
Arc length: x=4.5\mathrm{~m}
Angle: \theta=72^{\circ}
Substitute the known values into the formula for the arc length.
As you want to know the radius, use the formula which has ‘r’ as a variable.
Solve for the unknown value.
First, simplify the right hand side of the equation:
4.5=0.4\times\pi\times{r}
Divide both sides by 0.4\text{:}
11.25=\pi\times{r}
Divide both sides by \pi\text{:}
r=3.58\mathrm{~cm}=358\mathrm{~cm}
Teaching tips for arc of a circle
- Ensure students understand the basic parts of a circle, including the radius, diameter, circumference, center of a circle, and central angles.
- Use diagrams to show different types of arcs (minor and major arcs) and how they are measured.
- Facilitate discussions on how trigonometry and geometry intersect when dealing with arcs, promoting a deeper understanding.
- Provide worksheets with problems that require students to use the arc length formula and trigonometric functions to find missing values.
Easy mistakes to make
- Finding the length of the circumference not the length of the arc
Remember to find the fraction of the circle that makes the arc not just the circumference of the whole circle.
For example, use \cfrac{\theta}{360}\times\pi\times{d} or \cfrac{\theta}{360}\times{2}\times\pi\times{r} not \pi\times{d} or 2\times\pi\times{r} only.
- Confusing arc length with the area of the sector
Students may confuse the measurement of the arc’s length with the area of the sector. Emphasize that arc length is a distance along the circle’s circumference, while the area of the sector is measured in square units.
Related angles of a circle lessons
- Angles of a circle
- Segment of a circle
- Area of a segment of a circle
- Area of a sector
- Arc length formula
- Sector of a circle
- Perimeter of a sector
Practice arc of a circle questions
1. What part of a circle does the pink line show?

Segment

Major arc

Minor arc

Sector

Part of the circumference is called an arc. The pink line is more than half of the circumference, so it is a major arc.
2. The diagram shows a semicircle. What is the length of the curved edge, in terms of \pi.





A semicircle has an angle of 180^{\circ}. As the diameter d=8\mathrm{~cm},
\begin{aligned}x&=\cfrac{180}{360}\times\pi\times{8} \\\\ &=4\pi \\\\ &=12.57\mathrm{~cm}\text{ (2dp)} \end{aligned}
3. Find the length of the arc of the sector. Give your answer to the nearest tenth.
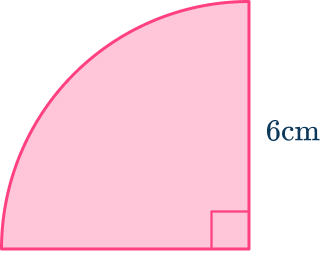




A quarter circle has an angle of 90^{\circ}. As the radius r=6\mathrm{~cm},
\begin{aligned}x&=\cfrac{90}{360}\times2\times\pi\times{6} \\\\ &=3\pi \\\\ &=9.42\mathrm{~cm}\text{ (2dp)} \end{aligned}
4. Find the length of the arc of the sector. Give your answer to the nearest tenth.
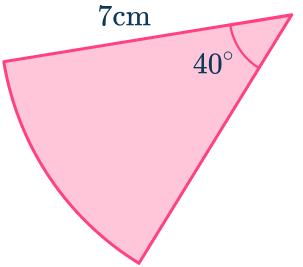




The sector has an angle of 40^{\circ}. As the radius r=7\mathrm{~cm},
\begin{aligned}x&=\cfrac{40}{360}\times2\times\pi\times{7} \\\\ &=4.9\mathrm{~cm}\text{ (1dp)} \end{aligned}
5. Find the length of the arc of the sector. Give your answer to the nearest tenth.
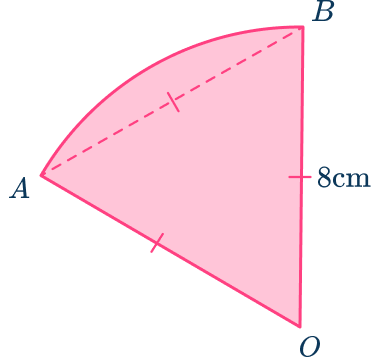




Substituting the values you know into the formula for the arc length, remembering \theta=60^{\circ} because this is an equilateral triangle.
\begin{aligned}x&=\cfrac{60}{360}\times2\times\pi\times{8} \\\\ &=8.4\mathrm{~cm}\text{ (1dp)} \end{aligned}
6. Find the angle of the sector with an arc length of 10\pi\mathrm{~cm} and a radius of 12\mathrm{~cm}.




Substituting the values you know into the formula for arc length,
\begin{aligned}10\pi&=\cfrac{\theta}{360}\times2\times\pi\times{12} \\\\ \cfrac{10}{12}&=\cfrac{\theta}{360} \\\\ \theta&=150^{\circ} \end{aligned}
Arc of a circle FAQs
An arc of a circle is a portion of the circumference of a circle.
An arc can be measured in two ways:
◦ Arc Length: The distance along the curved line of the arc, typically measured in linear units (for example, centimeters, inches). This can be measured using the arc length formula.
◦ Central Angle: The angle subtended by the arc at the center of the circle, measured in degrees or radians.
An inscribed angle is an angle formed by two chords (line segments) in a circle that share an endpoint on the circle. The vertex of the inscribed angle is on the circle, and the angle subtends an arc.
No, an arc of a circle cannot be a straight line. An arc is a curved segment of the circle’s circumference.
The next lessons are
- Circle theorems
- Prism shape
- Types of data
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!