High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Place value Powers of 10 Multiplication and division Decimals Exponents Significant figures

Math resources Algebra Scientific notation

Add and subtract scientific notation

Adding and subtracting scientific notation

Here you will learn about adding and subtracting scientific notation including what it is and how to solve problems.

Students will first learn about adding and subtracting scientific notation as part of expressions and equations in $8$ th grade.

What is adding and subtracting scientific notation?

Adding and subtracting with scientific notation is completing addition or subtraction between two numbers that are written in scientific notation.

Scientific notation is writing numbers in this form:

$a\times10^{n}$

Where $a$ is a number $1\leq{a}<10$ and $n$ is an integer (whole number).

Scientific notation makes calculations with very large numbers or small numbers quicker and easier to compute.

Calculations may take a common form of $a\times{10^n}\pm{b}\times{10^m}.$

Two strategies include:

Option $1\text{:}$ Adjust the value of a including the power of $10$ of one of the numbers written in scientific notation to match the other power of the other number, then calculate the addition or subtraction.
Option $2\text{:}$ Convert all values to ordinary numbers then carry out the calculation and convert back to scientific notation.

We will focus on the strategy in Option $1.$

What is adding and subtracting scientific notation?

Common Core State Standards

How does this relate to $8$ th grade math?

Grade 8 – Expressions and Equations (8.EE.A.4)
Perform operations with numbers expressed in scientific notation, including problems where both decimal and scientific notation are used.

Use scientific notation and choose units of appropriate size for measurements of very large or very small quantities (for example, use millimeters per year for seafloor spreading). Interpret scientific notation that has been generated by technology.

[FREE] Adding and Subtracting Scientific Notation Worksheet (Grade 8)

Use this worksheet to check your 8th grade students’ understanding of adding and subtracting scientific notation. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Adding and Subtracting Scientific Notation Worksheet (Grade 8)

Use this worksheet to check your 8th grade students’ understanding of adding and subtracting scientific notation. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

Adding and subtracting scientific notation

In order to perform operations by adding and subtracting scientific notation:

Convert the number(s) to have the same power of $\bf{10}.$
Add or subtract the non-zero digits.
Check your answer is in scientific notation.

Adding and subtracting scientific notation examples

Example 1: adding numbers in scientific notation

Calculate $4\times{10^4}+9\times{10^3}.$ Write your answer in scientific notation.

Convert the number(s) to have the same power of $\bf{10}.$

You can convert either number. Let’s convert $9\times{10^3}$ to match the power of $10$ for the other number $(10^4).$

To do this, multiply it by $10$ to add one to the power. To maintain the value of the number, you need to divide the non-zero number by $10.$

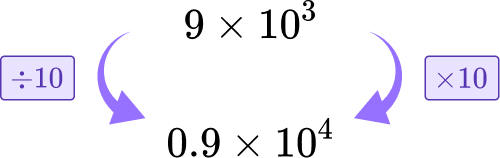
Adding and subtracting scientific notation 1 US

2Add or subtract the non-zero digits.

\begin{aligned}&4\times{10^4}+0.9\times{10^4} \\\\ &=(4+0.9)\times{10^4} \\\\ &=4.9\times{10^4} \end{aligned}

3Check your answer is in scientific notation.

Since $4.9$ is between $1$ and $10,$ you don’t need to adjust the power of $10.$

4\times{10^4}+9\times{10^3}=4.9\times{10^4}

Example 2: subtracting numbers in scientific notation

Calculate $7\times{10^{11}}-2\times{10^9}.$ Write your answer in scientific notation.

Convert the number(s) to have the same power of $\bf{10}.$

You can convert either number. Let’s convert $7\times{10^{11}}$ to be $10^9.$

$7\times{10^{11}}=70\times{10^{10}}=700\times{10^9}$

Add or subtract the non-zero digits.

\begin{aligned}&700\times{10^9}-2\times{10^9} \\\\ &=(700-2)\times{10^9} \\\\ &=698\times{10^9} \end{aligned}

Check your answer is in scientific notation.

$698$ is not between $1$ and $10$ , so convert $698\times{10^9}$ back to scientific notation.

\begin{aligned}&698\times{10^9} \\\\ &=69.8\times{10^8} \\\\ &=6.98\times{10^7} \end{aligned}

$7\times{10^{11}}-2\times{10^9}=6.98\times{10^7}$

Example 3: adding in scientific notation

Calculate $5.8\times{10^6}+6.07\times{10^5}.$ Write your answer in scientific notation.

Convert the number(s) to have the same power of $\bf{10}.$

You can convert either number. Let’s convert $5.8\times{10^6}$ to be $10^5.$

To do this, multiply it by $10$ to add one to the power. To maintain the value of the number, you need to divide the non-zero number by $10.$

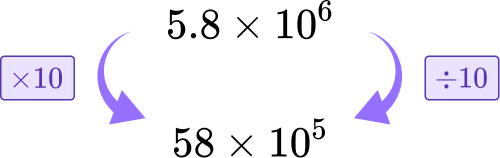
Adding and subtracting scientific notation 2 US

Add or subtract the non-zero digits.

\begin{aligned}&58\times{10^5}+6.07\times{10^5} \\\\ &=(58+6.07)\times{10^5} \\\\ &=64.07\times{10^5} \end{aligned}

Check your answer is in scientific notation.

$64.07$ is not between $1$ and $10$ , so convert $64.07\times{10^5}$ back to scientific notation.

\begin{aligned}&64.07\times{10^5} \\\\ &=6.407\times{10^6} \end{aligned}

$5.8\times{10^6}+6.07\times{10^5}=6.407\times{10^6}$

Example 4: subtracting in scientific notation

Calculate $4.4\times{10^{15}}-1.8\times{10^{13}}.$ Write your answer in scientific notation.

Convert the number(s) to have the same power of $\bf{10}.$

You can convert either number. Let’s convert $4.4\times{10^{15}}$ to be $10^{13}.$

$4.4\times{10^{15}}=44\times{10^{14}}=440\times{10^{13}}$

Add or subtract the non-zero digits.

\begin{aligned}&440\times{10^{13}}-1.8\times{10^{13}} \\\\ &=(440-1.8)\times{10^{13}} \\\\ &=438.2\times{10^{13}} \end{aligned}

Check your answer is in scientific notation.

$438.2$ is not between $1$ and $10.$ Convert $438.2\times{10^{13}}$ back to scientific notation.

\begin{aligned}&438.2\times{10^{13}} \\\\ &=43.82\times{10^{14}} \\\\ &=4.382\times{10^{15}} \end{aligned}

$4.4\times{10^{15}}-1.8\times{10^{13}}=4.382\times{10^{15}}$

Example 5: adding in scientific notation

Calculate $3.2\times{10^4}+5.78\times{10^3}.$ Write your answer in scientific notation.

Convert the number(s) to have the same power of $\bf{10}.$

You can convert either number. Let’s convert $5.78\times{10^3}$ to be $10^4.$

To do this, multiply it by $10$ to add one to the power. To maintain the value of the number, you need to divide the non-zero number by $10.$

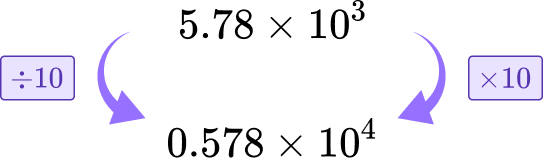
Adding and subtracting scientific notation 3 US

Add or subtract the non-zero digits.

\begin{aligned}&3.2\times{10^4}+0.578\times{10^4} \\\\ &=(3.2+0.578)\times{10^4} \\\\ &=3.778\times{10^4} \end{aligned}

Check your answer is in scientific notation.

$3.778$ is between $1$ and $10.$

$3.2\times{10^4}+5.78\times{10^3}=3.778\times{10^4}$

Example 6: subtracting in scientific notation

Calculate $1.2\times{10^{-5}}-6.6\times{10^{-6}}.$ Write your answer in scientific notation.

Convert the number(s) to have the same power of $\bf{10}.$

You can convert either number. Let’s convert $1.2\times{10^{-5}}$ to be $10^{-6}.$

$1.2\times{10^{-5}}=12\times{10^{-6}}$

Add or subtract the non-zero digits.

\begin{aligned}&12\times{10^{-6}}-6.6\times{10^{-6}} \\\\ &=(12-6.6)\times{10^{-6}} \\\\ &=5.4\times{10^{-6}} \end{aligned}

Check your answer is in scientific notation.

$5.4$ is between $1$ and $10.$

$1.2\times{10^{-5}}-6.6\times{10^{-6}}=5.4\times{10^{-6}}$

Teaching tips for adding and subtracting scientific notation

Spend time reviewing exponential notation and rules for operating with exponent before teaching students how to add and subtract with scientific notation.

Compare adding and subtracting numbers in scientific notation with unit conversions for measurement operations. For example, if you wanted to add $20 \, mm$ and $50 \, m,$ you would first need them to be in the same units.

Converting $50 \, m$ to $50,000 \, mm$ shows the same value, but now in units that match $20 \, mm.$ This means you can add $50,000$ and $20$ to solve.

The same is true for scientific notation. In order to add or subtract, the numbers need to have the same “units” or powers of $10.$

Begin with worksheets that have practice problems with whole number coefficients. As students master whole number coefficients, move onto calculations that involve decimal numbers.

To help students struggling with adding or subtracting decimals, give them access to an adding and subtracting decimals tutorial (a full video or an abbreviated step by step guide) and access to a scientific calculator to simplify the solving process for them.

Easy mistakes to make

Not converting the first number, when it is too large or too small
After adding or subtracting in scientific notation, make sure the first part of each number is $1\leq{n}<10.$ If not, use powers of $10$ to convert.

Getting confused when converting numbers between powers of $\bf{10}$
Each place value is $10$ times smaller than the place to the left and $10$ times larger than the place to the right, which makes the digits “move” around the decimal point a certain number of places aftering adding or subtracting by multiples of ten.

For example,
In the number $0.081\times{10^9}, \, 0.081$ is not between $1$ and $10.$ It needs to be converted to be in scientific notation.

$\begin{aligned}&\left(8.1\times{10^{-2}}\right)\times{10^9} \\\\ &=8.1\times\left({10^{-2}}\times{10^9}\right) \\\\ &=8.1\times\left({10^{-2+9}}\right) \\\\ &=8.1\times{10^7} \end{aligned}$

Forgetting the value of negative exponents
Decimal positions can be represented by powers of $10$ with negative exponents and each has an equivalent fraction.
For example,

$\begin{aligned} 10^{-1}&=\cfrac{1}{10} \\\\ 10^{-2}&=\cfrac{1}{100} \\\\ 10^{-3}&=\cfrac{1}{1,000} \\\\ 10^{-4}&=\cfrac{1}{10,000} \end{aligned}$

Practice adding and subtracting scientific notation questions

21\times{10^{12}}

7.03\times{10^5}

703\times{10^7}

3.07\times{10^7}

You can convert either number. Let’s convert $3\times{10^7}$ to be $10^5.$

3\times{10^7}=30\times{10^6}=300\times{10^5}

Now we can solve the equivalent equation.

\begin{aligned}&300\times{10^5}+7\times{10^5} \\\\ &=(300+7)\times{10^5} \\\\ &=307\times{10^5} \end{aligned}

$307$ is not between $1$ and $10.$

Convert $307 \times 10^5$ back to scientific notation.

\begin{aligned}&307\times{10^5} \\\\ &=30.7\times{10^6} \\\\ &=3.07\times{10^7} \end{aligned}

68\times{10^9}

6.8\times{10^9}

5\times{10^1}

5\times{10^8}

You can convert either number. Let’s convert $2\times{10^8}$ to be $10^9.$

2\times{10^8}=0.2\times{10^9}

Now we can solve the equivalent equation.

\begin{aligned}&7\times{10^9}-0.2\times{10^9} \\\\ &=(7-0.2)\times{10^9} \\\\ &=6.8\times{10^9} \end{aligned}

$6.8$ is between $1$ and $10.$

8.12\times{10^{24}}

4.87\times{10^{13}}

4.93\times{10^{11}}

3.27\times{10^{13}}

You can convert either number. Let’s convert $3.22\times{10^{13}}$ to be $10^{11}.$

3.22\times{10^{13}}=32.2\times{10^{12}}=322\times{10^{11}}

Now we can solve the equivalent equation.

\begin{aligned}&4.9\times{10^{11}}+322\times{10^{11}} \\\\ &=(4.9+322)\times{10^{11}} \\\\ &=326.9\times{10^{11}} \end{aligned}

$326.9$ is not between $1$ and $10.$

Convert $326.9\times{10^{11}}$ back to scientific notation.

\begin{aligned}&326.9\times{10^{11}} \\\\ &=32.69\times{10^{12}} \\\\ &=3.269\times{10^{13}} \end{aligned}

$3.269$ rounded to the nearest hundredth is $3.27$

5.195\times{10^{10}}

2.45\times{10^1}

25\times{10^{10}}

25\times{10^{8}}

You can convert either number. Let’s convert $3.05\times{10^9}$ to be $10^{10}.$

3.05\times{10^9}=0.305\times{10^{10}}

Now we can solve the equivalent equation.

\begin{aligned}&5.5\times{10^{10}}-0.305\times{10^{10}} \\\\ &=(5.5-0.305)\times{10^{10}} \\\\ &=5.195\times{10^{10}} \end{aligned}

$5.195$ is between $1$ and $10.$

1.69\times{10^2}

15.71\times{10^{12}}

7.10\times{10^{14}}

8.77\times{10^7}

You can convert either number. Let’s convert $8.7\times{10^7}$ to be $10^5.$

8.7\times{10^7}=87\times{10^6}=870\times{10^5}

Now we can solve the equivalent equation.

\begin{aligned}&870\times{10^5}+7.01\times{10^5} \\\\ &=(870+7.01)\times{10^5} \\\\ &=877.01\times{10^5} \end{aligned}

$877.01$ is not between $1$ and $10.$

Convert $877.01\times{10^5}$ back to scientific notation.

\begin{aligned}&877.01\times{10^5} \\\\ &=87.701\times{10^6} \\\\ &=8.7701\times{10^7} \end{aligned}

$8.7701$ rounded to the nearest hundredth is $8.77$

– \, 6.1\times{10^4}

– \, 6.1\times{10^0}

1.09928\times{10^2}

10992.8\times{10^{-2}}

1.1\times{10^2}=11\times{10^1}=110\times{10^0}=1100\times{10^{-1}}=11000\times{10^{-2}}

\begin{aligned}&1.1\times{10^2}-7.2\times{10^{-2}} \\\\ &=11000\times{10^{-2}}-7.2\times{10^{-2}} \\\\ &=(11000-7.2)\times{10^{-2}} \\\\ &=10992.8\times{10^{-2}} \\\\ &=1099.28\times{10^{-1}} \\\\ &=109.928\times{10^0} \\\\ &=10.9928\times{10^1} \\\\ &=1.09928\times{10^2} \end{aligned}

Scientific notation FAQs

What is the procedure for dividing scientific notation?

When dividing numbers written in scientific notation, divide the first numbers, $a$ and $b,$ by each other and the powers of $10$ by each other. Then combine both quotients to show the answer in scientific notation.

Do students use scientific notation in high school?

Yes, it is used in mathematics classrooms and in science classes.

What exponent represents square roots?

The exponent $\cfrac{1}{2}$ is used to show a square root. Scientific notation only uses integer powers.

The next lessons are

Factoring
Quadratic graphs
Radical

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.