High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Ratios Whole numbers Improper fraction to mixed number Numerator and denominator

Math resources Number and quantity Fractions operations

Multiplying fractions

Here you will learn about multiplying fractions including how to multiply fractions together, multiply fractions by whole numbers, and multiply mixed numbers.

Students will first learn about multiplying unit fractions and whole numbers as part of number and operations in fractions in 4th grade. They will build on this understanding and multiply fractions by fractions as a part of number and operations in fractions in 5th grade.

What is multiplying fractions?

Multiplying fractions is multiplying one or more numbers that are in fraction form. Fractions can be multiplied using models or the algorithm.

For example…

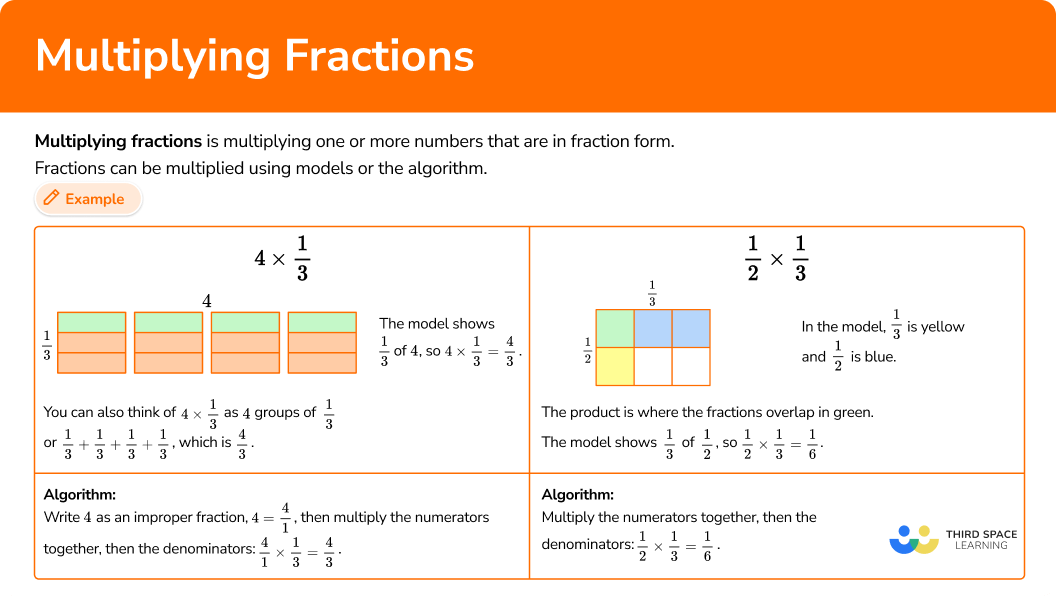
Multiplying a unit fraction by a whole number

$4 \times \cfrac{1}{3}$

Using models:

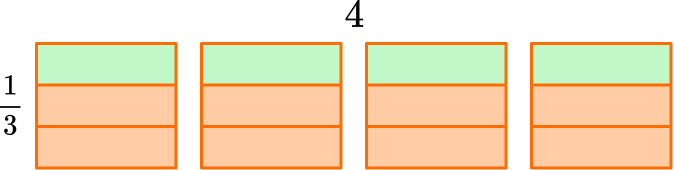
The model shows $\cfrac{1}{3}$ of $4,$ so $4 \times \cfrac{1}{3} = \cfrac{4}{3}.$

You can also think of $4 \times \cfrac{1}{3}$ as $4$ groups of $\cfrac{1}{3}$ or $\cfrac{1}{3}+\cfrac{1}{3}+\cfrac{1}{3}+\cfrac{1}{3},$ which is $\cfrac{4}{3}.$

Using the algorithm:

Write $4$ as an improper fraction, $4=\cfrac{4}{1},$ then multiply the numerators together, then the denominators:

$\cfrac{4}{1} \times \cfrac{1}{3}=\cfrac{4}{3}.$

Multiplying a fraction by a whole number

$3 \times \cfrac{2}{5}$

Using models:

The model shows $\cfrac{2}{5}$ of $3,$ so $3 \times \cfrac{2}{5}=\cfrac{6}{5}.$

You can also think of $3 \times \cfrac{2}{5}$ as $3$ groups of $\cfrac{2}{5}$ or $\cfrac{2}{5}+\cfrac{2}{5}+\cfrac{2}{5},$ which is $\cfrac{6}{5}.$

Using the algorithm:

Write $3$ as an improper fraction, $3=\cfrac{3}{1},$ then multiply the numerators together, then the denominators:

$\cfrac{3}{1} \times \cfrac{2}{5}=\cfrac{6}{5}.$

Multiplying fractions by fractions

$\cfrac{1}{2} \times \cfrac{1}{3}$

Using models:

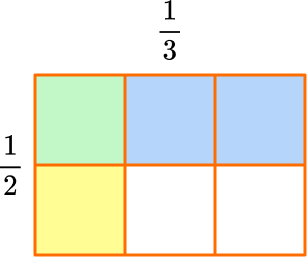
In the model, $\cfrac{1}{3}$ is yellow and $\cfrac{1}{2}$ is blue.

The product is where the fractions overlap in green.

The model shows $\cfrac{1}{3}$ of $\cfrac{1}{2},$ so $\cfrac{1}{2} \times \cfrac{1}{3}=\cfrac{1}{6}.$

Using the algorithm:

Multiply the numerators together, then the denominators: $\cfrac{1}{2} \times \cfrac{1}{3}=\cfrac{1}{6}.$

Multiplying mixed numbers

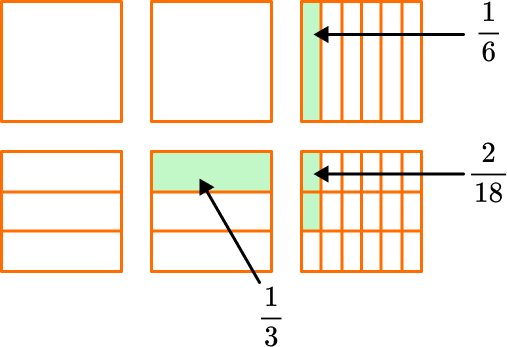
1 \cfrac{2}{3} \times 2 \cfrac{1}{6}

Using models:

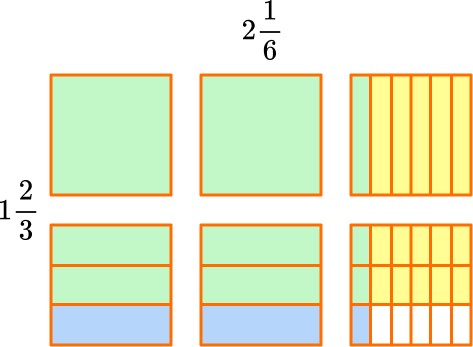
In the model, $1 \cfrac{2}{3}$ is yellow and $2 \cfrac{1}{6}$ is blue.

The product is where the mixed numbers overlap.

The model shows $1 \cfrac{2}{3}$ groups of $2 \cfrac{1}{6}.$

Notice you have $2$ wholes and moving $\cfrac{1}{3}$ to $\cfrac{2}{3}$ is $\cfrac{3}{3}$ which makes another whole.

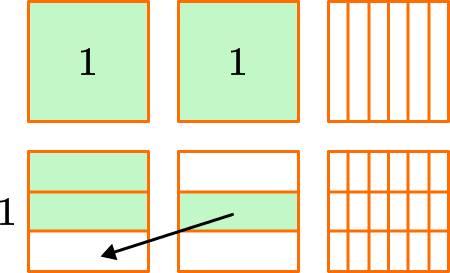
Then there is also $\cfrac{1}{3}, \cfrac{1}{6}$ and $\cfrac{2}{18}.$

To find the product, you add these fractions to the $3$ wholes.

\begin{aligned} & 3+\cfrac{1}{3}+\cfrac{1}{6}+\cfrac{2}{18} \\\\ & =3+\cfrac{1 \times 6}{3 \times 6}+\cfrac{1 \times 3}{6 \times 3}+\cfrac{2}{18} \\\\ & =3+\cfrac{6}{18}+\cfrac{3}{18}+\cfrac{2}{18} \\\\ & =3 \cfrac{11}{18} \end{aligned}

Using the algorithm:

Convert the mixed numbers to improper fractions.

$\hspace{1cm} 2 \cfrac{1}{6}=\cfrac{13}{6} \hspace{1cm}$ and $\hspace{1cm} 1 \cfrac{2}{3}=\cfrac{5}{3}$

Multiply the numerators together, then the denominators: $\cfrac{13}{6} \times \cfrac{5}{3}=\cfrac{65}{18}.$

Write $\cfrac{65}{18}$ as a mixed number: $3 \cfrac{11}{18}.$

What is multiplying fractions?

$What is multiplying fractions?$

Common Core State Standards

How does this relate to 4th grade math and 5th grade math?

Grade 4 – Number and Operations – Fractions (4.NF.B.4b)
Understand a multiple of $\cfrac{a}{b}$ as a multiple of $\cfrac{1}{b},$ and use this understanding to multiply a fraction by a whole number.

Grade 5 – Number and Operations – Fractions (5.NF.B.4b)
Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.

How to multiply fractions

In order to multiply fractions with models:

Draw one fraction horizontally and the other vertically.
Connect the fractions all the way across with $\bf{2}$ different colors.
Count the overlap.
If possible, simplify or convert to a mixed number.

In order to multiply fractions with the algorithm:

Multiply the numerators together.
Multiply the denominators together.
If possible, simplify or convert to a mixed number.

In order to multiply whole numbers or mixed numbers by fractions with the algorithm:

Convert to improper fractions.
Multiply the numerators together.
Multiply the denominators together.
If possible, simplify or convert to a mixed number.

[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of fraction operations. 10+ questions with answers covering a range of 4th to 6th grade fraction operations topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)

DOWNLOAD FREE

Multiplying fractions examples

Example 1: multiplying a fraction by a fraction with a model

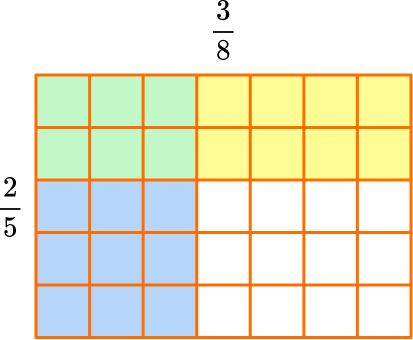
Solve $\cfrac{2}{5} \times \cfrac{3}{8}$ with a model.

Draw one fraction horizontally and the other vertically.

Draw a rectangle. Divide one side into fifths.

Divide the other side into eighths.

2Connect the fractions all the way across with $\bf{2}$ different colors.

Shade in $\cfrac{2}{5}$ with yellow and $\cfrac{3}{8}$ with blue.

3Count the overlap.

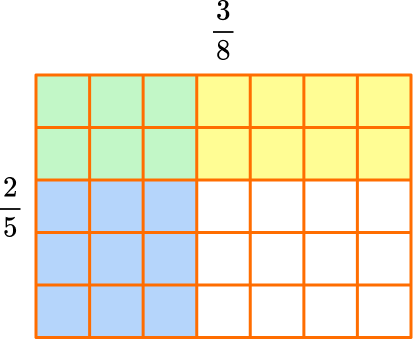
The product is where the fractions overlap in green.

The model shows $\cfrac{3}{8}$ of $\cfrac{2}{5},$ so $\cfrac{2}{5} \times \cfrac{3}{8}=\cfrac{6}{40},$ because there are $6$ green squares and the whole has $40$ squares in total.

4If possible, simplify or convert to a mixed number.

The product can be simplified.

Both $6$ and $40$ have a factor of $2,$ so they can be divided by $2$ : $\cfrac{6 \; \div \; 2}{40 \; \div \; 2}=\cfrac{3}{20}.$

So, $\cfrac{2}{5} \times \cfrac{3}{8}=\cfrac{6}{40} \,$ or $\, \cfrac{3}{20}.$

Example 2: multiplying a fraction by a fraction with a model

Solve $\cfrac{3}{4} \times \cfrac{1}{6}$ with a model.

Draw one fraction horizontally and the other vertically.

Draw a rectangle. Divide one side into fourths.

Divide the other side into eighths.

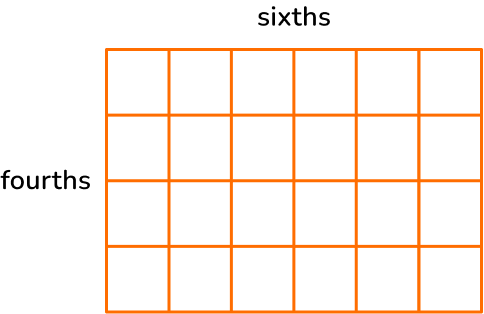
Connect the fractions all the way across with $\bf{2}$ different colors.

Shade in $\cfrac{3}{4}$ with yellow and $\cfrac{1}{6}$ with blue.

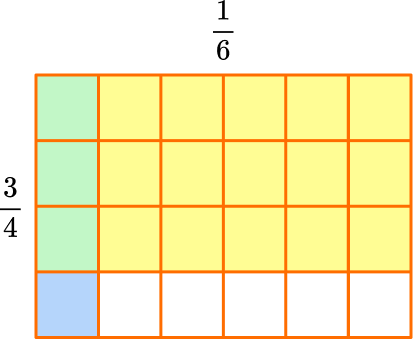
Count the overlap.

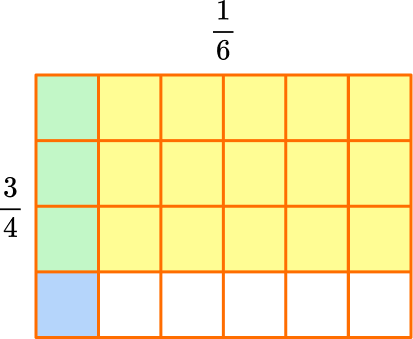
The product is where the fractions overlap in green.

The model shows $\cfrac{1}{6}$ of $\cfrac{3}{4},$ so $\cfrac{3}{4} \times \cfrac{1}{6}=\cfrac{3}{24},$ because there are $3$ green squares and the whole has $24$ squares in total.

If possible, simplify or convert to a mixed number.

The product can be simplified.

Both $3$ and $24$ have a factor of $3,$ so they can be divided by $3$ : $\cfrac{3 \; \div \; 3}{24 \; \div \; 3}=\cfrac{1}{8}.$

So, $\cfrac{3}{4} \times \cfrac{1}{6}=\cfrac{3}{24} \,$ or $\, \cfrac{1}{8}.$

Example 3: multiplying a fraction by fraction with the algorithm

Solve $\cfrac{5}{12} \times \cfrac{2}{3}.$

Multiply the numerators together.

$\cfrac{5}{12} \times \cfrac{2}{3}=\cfrac{10}{}$

Multiply the denominators together.

$\cfrac{5}{12} \times \cfrac{2}{3}=\cfrac{10}{36}$

If possible, simplify or convert to a mixed number.

The product can be simplified.

Both $10$ and $36$ have a factor of $2,$ so they can be divided by $2$ : $\cfrac{10 \; \div \; 2}{36 \; \div \; 2}=\cfrac{5}{18}.$

So, $\cfrac{5}{12} \times \cfrac{2}{3}=\cfrac{10}{36} \,$ or $\, \cfrac{5}{18}.$

Example 4: multiplying a fraction by fraction with the algorithm

Solve $\cfrac{1}{2} \times \cfrac{7}{10}.$

Multiply the numerators together.

$\cfrac{1}{2} \times \cfrac{7}{10}=\cfrac{7}{}$

Multiply the denominators together.

$\cfrac{1}{2} \times \cfrac{7}{10}=\cfrac{7}{20}$

If possible, simplify or convert to a mixed number.

The product cannot be simplified. $7$ and $20$ only have a common factor of $1.$

So, $\cfrac{1}{2} \times \cfrac{7}{10}=\cfrac{7}{20}.$

Example 5: multiplying a whole number by fraction with the algorithm

Solve $\cfrac{2}{9} \times 4.$

Convert to improper fractions.

Write $4$ as an improper fraction, $4=\cfrac{4}{1}.$

Multiply the numerators together.

$\cfrac{2}{9} \times \cfrac{4}{1}=\cfrac{8}{}$

Multiply the denominators together.

$\cfrac{2}{9} \times \cfrac{4}{1}=\cfrac{8}{9}$

If possible, simplify or convert to a mixed number.

The product cannot be simplified. $8$ and $9$ only have a common factor of $1.$

So, $\cfrac{2}{9} \times \cfrac{4}{1}=\cfrac{8}{9}.$

Example 6: multiplying a mixed number by fraction with the algorithm

Solve $\cfrac{3}{8} \times 3 \cfrac{5}{8}.$

Convert to improper fractions.

Convert the mixed number to an improper fraction.

$3 \cfrac{5}{8}=\cfrac{29}{8}$

Multiply the numerators together.

$\cfrac{3}{8} \times \cfrac{29}{8}=\cfrac{87}{}$

Multiply the denominators together.

$\cfrac{3}{8} \times \cfrac{29}{8}=\cfrac{87}{64}$

If possible, simplify or convert to a mixed number.

The numerator is greater than the denominator, so the improper fraction can be converted to a mixed number.

$\cfrac{87}{64}=1 \cfrac{23}{64}$

The product cannot be simplified. $23$ and $64$ only have a common factor of $1.$

So, $\cfrac{3}{8} \times \cfrac{29}{8}=\cfrac{87}{64} \,$ or $\, 1 \cfrac{23}{64}$

Teaching tips for multiplying fractions

Multiplication of fractions is challenging for elementary students. This type of multiplication does not lend itself well to the idea of repeated addition, which students rely on for whole number multiplication. Utilize hands-on visual models and/or digital models as much as possible so that students can understand what multiplication of fractions is and why the algorithm works.

Explore patterns so that students can make sense of the simple steps involved in multiplying fractions.

Practice worksheets alone will not develop a deep understanding of this topic. Incorporating visual models, hands-on activities, and digital games are very effective alternatives to just using fraction multiplication worksheets.

Our favorite mistakes

Confusing multiplying and division multiplication rules
When multiplying, it is not necessary to flip the second fraction (use the reciprocal) like it is when dividing.
For example,

Cross multiplying
If students have been introduced to cross multiplying, they may get confused and use it when multiplying two fractions.
For example,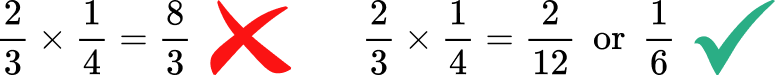

Finding the common denominator
It is not necessary to find a common denominator when multiplying fractions like it is for adding or subtracting fractions. While it will not create an incorrect answer, it creates unnecessary work and more opportunities to make mistakes.
For example,
No common denominatorCommon denominator
created: created: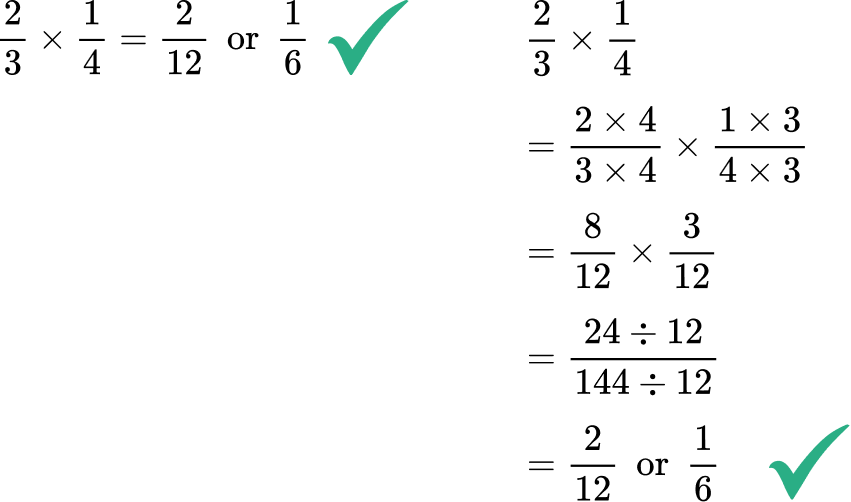

Practice multiplying fractions questions

\cfrac{10}{13}

\cfrac{9}{30}

\cfrac{10}{27}

\cfrac{37}{30}

To solve using a model, draw a rectangle. Divide one side into thirds.

Multiplying Fractions image 20 US

Divide the other side into tenths.

Multiplying Fractions image 21 US

Shade in $\cfrac{1}{3}$ with blue and $\cfrac{9}{10}$ with yellow.

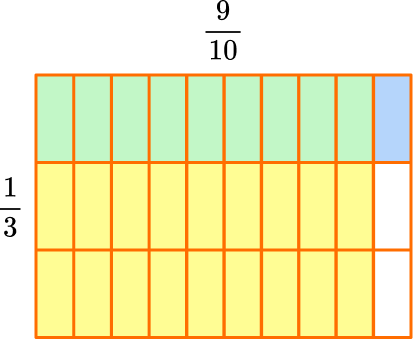
Multiplying Fractions image 22 US

The product is where the fractions overlap in green.

The model shows $\cfrac{9}{10}$ of $\cfrac{1}{3},$ so $\cfrac{1}{3} \times \cfrac{9}{10}=\cfrac{9}{30},$ because there are $9$ green squares and the whole has $30$ squares in total.

The product can be simplified.

Both $9$ and $30$ have a factor of $3,$ so they can be divided by $3$ : $\cfrac{9 \; \div \; 3}{30 \; \div \; 3}=\cfrac{3}{10}.$

So, $\cfrac{1}{3} \times \cfrac{9}{10}=\cfrac{9}{30} \,$ or $\, \cfrac{3}{10}.$

\cfrac{20}{30}

\cfrac{25}{24}

\cfrac{9}{11}

\cfrac{49}{30}

To solve using a model, draw a rectangle. Divide one side into sixths.

Multiplying Fractions image 23 US

Divide the other side into fifths.

Multiplying Fractions image 24 US

Shade in $\cfrac{5}{6}$ with yellow and $\cfrac{4}{5}$ with blue.

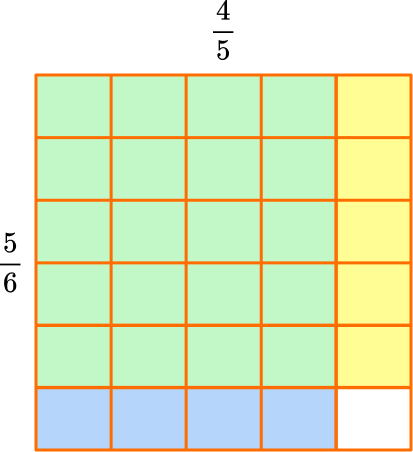
Multiplying Fractions image 25 US

The product is where the fractions overlap in green.

The model shows $\cfrac{4}{5}$ of $\cfrac{5}{6},$ so $\cfrac{5}{6} \times \cfrac{4}{5}=\cfrac{20}{30},$ because there are $20$ green squares and the whole has $30$ squares in total.

The product can be simplified.

Both $20$ and $30$ have a factor of $10,$ so they can be divided by $10$ : $\cfrac{20 \; \div \; 10}{30 \; \div \; 10}=\cfrac{2}{3}.$

So, $\cfrac{5}{6} \times \cfrac{4}{5}=\cfrac{20}{30} \;$ or $\; \cfrac{2}{3}.$

\cfrac{110}{36}

\cfrac{55}{18}

\cfrac{14}{22}

\cfrac{33}{120}

Multiply the numerators together: $\cfrac{11}{12} \times \cfrac{3}{10}=\cfrac{33}{}.$

Then, multiply the denominators together: $\cfrac{11}{12} \times \cfrac{5}{10}=\cfrac{33}{120}.$

The product cannot be simplified. $33$ and $120$ only have a common factor of $1.$

S0, $\cfrac{11}{12} \times \cfrac{5}{10}=\cfrac{33}{120}.$

\cfrac{2}{55}

\cfrac{10}{55}

\cfrac{10}{11}

\cfrac{57}{9}

Write $5$ as an improper fraction, $5=\cfrac{5}{1}.$

Then, multiply the numerators together: $\cfrac{2}{11} \times \cfrac{5}{1}=\cfrac{10}{}.$

Then, multiply the denominators together: $\cfrac{2}{11} \times \cfrac{5}{1}=\cfrac{10}{11}.$

The product cannot be simplified. $10$ and $11$ only have a common factor of $1.$

So, $\cfrac{2}{11} \times \cfrac{5}{1}=\cfrac{10}{11}.$

4 \cfrac{2}{5}

3 \cfrac{2}{15}

2 \cfrac{17}{18}

2 \cfrac{13}{15}

Convert the mixed numbers to improper fractions.

$\hspace{1cm} 3 \cfrac{2}{3}=\cfrac{11}{3} \hspace{1cm}$ and $\hspace{1cm} 1 \cfrac{1}{5}=\cfrac{6}{5}$

Multiplying Fractions image 26 US

Then, multiply the numerators together: $\cfrac{11}{3} \times \cfrac{6}{5}=\cfrac{66}{}.$

Then, multiply the denominators together: $\cfrac{11}{3} \times \cfrac{6}{5}=\cfrac{66}{15}.$

The numerator is greater than the denominator, so the improper fraction can be converted to a mixed number.

\cfrac{66}{15}=4 \cfrac{6}{15}

The product can be simplified.

Both $6$ and $15$ have a factor of $3,$ so they can be divided by $3$ : $\cfrac{6 \; \div \; 3}{15 \; \div \; 3}=\cfrac{2}{5}.$

So, $\cfrac{11}{3} \times \cfrac{6}{5}=\cfrac{66}{15} \;$ or $\; 4 \cfrac{2}{5}.$

3

4

10

12

The area of a rectangle is $\text { base } \times \text { height }$ therefore to work out the area of the wall we need to calculate $4 \cfrac{2}{5} \times 2 \cfrac{1}{4}.$

Convert the mixed numbers to improper fractions.

$\hspace{1cm} 4 \cfrac{2}{5}=\cfrac{22}{5} \hspace{1cm}$ and $\hspace{1cm} 2 \cfrac{1}{4}=\cfrac{9}{4}$

Multiplying Fractions image 27 US

Then, multiply the numerators together: $\cfrac{22}{5} \times \cfrac{9}{4}=\cfrac{198}{}.$

Then, multiply the denominators together: $\cfrac{22}{5} \times \cfrac{9}{4}=\cfrac{198}{20}.$

The numerator is greater than the denominator, so the improper fraction can be converted to a mixed number.

\cfrac{198}{20}=9 \cfrac{18}{20}

The product can be simplified.

Both $2$ and $20$ have a factor of $2,$ so they can be divided by $2$ : $\cfrac{18 \; \div \; 2}{20 \; \div \; 2}=\cfrac{9}{10}.$

So, $\cfrac{22}{5} \times \cfrac{9}{4}=\cfrac{198}{20} \;$ or $\; 9 \cfrac{9}{10}.$

We have $9 \cfrac{9}{10} \mathrm{m}^{2}$ of wall to paint and each tin can cover $3 m^2.$

$3$ tins can cover $9 m^2\left(3 \times 3 m^2\right),$ therefore you need to buy $4$ tins of paint to cover the entire $9 \cfrac{9}{10} m^2$ wall.

Multiplying fractions FAQs

Is multiplying fractions the same as dividing fractions?

No, when you multiply fractions, you multiply the fractions together and do not take the reciprocal of the second fraction. When you divide fractions, you multiply by the reciprocal of the divisor.

What vocabulary is used for multiplying fractions?

It is important to know the following terms…
◌ Denominator: the bottom number
◌ Numerator: the top number
◌ Product: the answer to a multiplication equation

Does the final answer have to be in lowest terms?

While students are encouraged to use the greatest common factor (GCF) to simplify the products to their lowest terms, it is not a requirement for their understanding of this skill. Additionally, each state has different expectations of when students should use lowest terms. Refer to state standards for clarification.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.