High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Prime numbersUnderstanding multiplication
ExponentsLeast common multiple
Here you will learn about the least common multiple, including a review on prime factorization and how to use it to find the least common multiple
Students will first learn about the least common multiple as part of the number system in 6th grade.
What is the least common multiple?
The least common multiple (LCM) is the smallest number that two or more integers share as a multiple. The name itself tells you what the skill is:
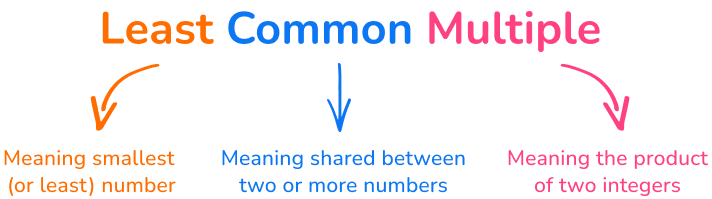
Take, for example, 4 and 6.
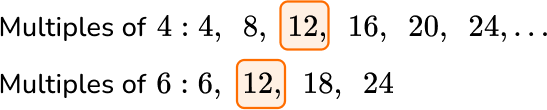
By listing the multiples of 4 and 6, you can see that the first common multiple that occurs in each list is 12. So, the least common multiple of 4 and 6 is 12.
You may also notice that 24 occurs in both lists. This is a common multiple, but not the least common multiple.
The Prime Factorization Method
Calculating the least common multiple becomes more complicated for larger numbers. Listing all the multiples of each number can be time-consuming and it is easy to miscalculate a multiple.
To make it simpler, you can use the prime factors of both numbers. You can use prime factors and a Venn diagram to calculate the Least Common Multiple.
You need to write out the prime factorization of each number fully and then put the numbers into the Venn diagram by looking for pairs.
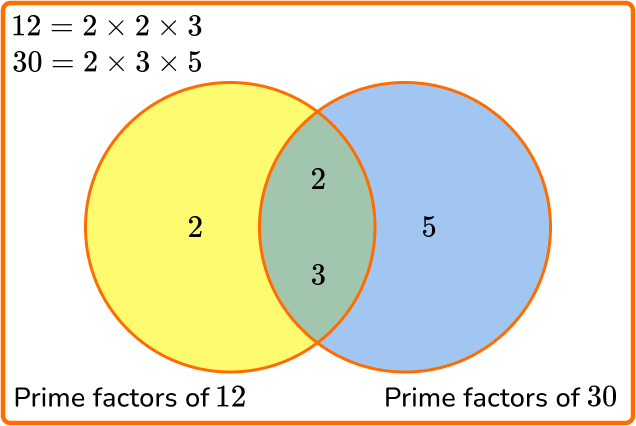
Here, you have the prime factors of 12 and 30.
- The yellow section represents the prime factors of 12 that are not prime factors of 30 (which is just the prime factor of 2).
- The blue section represents the prime factors of 30 that are not prime factors of 12 (which is just the prime factor of 5).
- The green intersection represents the prime factors of 12 and 30 \; (2 and 3).
The least common multiple of 12 and 30 is equal to the product of all the factors viewed in the Venn diagram.
The least common multiple is 2 \times 2 \times 3 \times 5= 60.
What is the least common multiple?

Common Core State Standards
How does this relate to 6th grade math?
- Grade 6 – The Number System (6.NS.B.4)
Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers
How to calculate the least common multiple
In order to calculate the least common multiple for two or more numbers:
- State the product of prime factors of each number.
- Write all the prime factors into the Venn diagram for each number.
- Multiply each prime factor in the Venn diagram to find the LCM.
![[FREE] Least Common Multiple Worksheet (Grade 6)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Grades-6-to-8-Least-Common-Multiple-Worksheet-listing-image.png)
[FREE] Least Common Multiple Worksheet (Grade 6)
![[FREE] Least Common Multiple Worksheet (Grade 6)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Grades-6-to-8-Least-Common-Multiple-Worksheet-listing-image.png)
Use this worksheet to check your grade 6 students’ understanding of least common multiples. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Least Common Multiple Worksheet (Grade 6)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Grades-6-to-8-Least-Common-Multiple-Worksheet-listing-image.png)
[FREE] Least Common Multiple Worksheet (Grade 6)
![[FREE] Least Common Multiple Worksheet (Grade 6)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Grades-6-to-8-Least-Common-Multiple-Worksheet-listing-image.png)
Use this worksheet to check your grade 6 students’ understanding of least common multiples. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREELeast common multiple examples
Example 1: two simple composite numbers.
Calculate the least common multiple of 18 and 24.
- State the product of prime factors of each number.
\begin{aligned} & 18=2 \times 3 \times 3 \\\\ & 24=2 \times 2 \times 2 \times 3 \end{aligned}
2Write all the prime factors into the Venn diagram for each number.
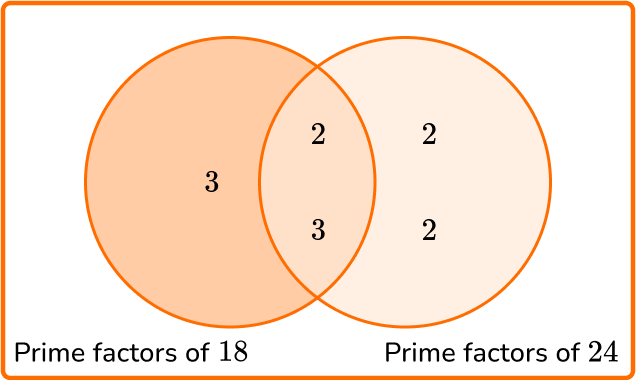
3Multiply each prime factor in the Venn diagram to find the LCM.
LCM =3 \times 2 \times 3 \times 2 \times 2=72
Example 2: one composite number is a factor of the other
Calculate the least common multiple of 14 and 56.
State the product of prime factors of each number.
\begin{aligned} & 14=2 \times 7 \\\\ & 56=2 \times 2 \times 2 \times 7 \end{aligned}
Write all the prime factors into the Venn diagram for each number.
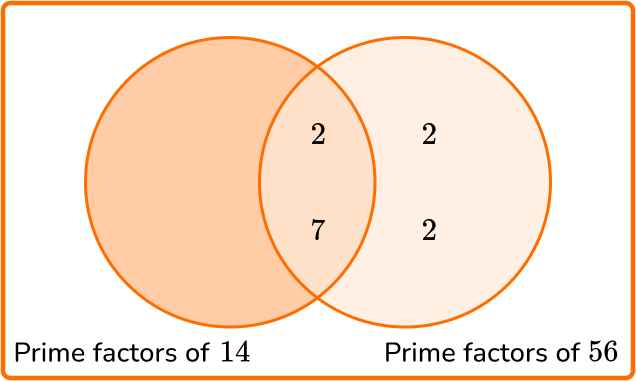
Multiply each prime factor in the Venn diagram to find the LCM.
LCM =2 \times 7 \times 2 \times 2=56
Example 3: calculate the prime factorization first
Given that 90=2 \times 3^2 \times 5 in exponent form, work out the least common multiple of 54 and 90.
State the product of prime factors of each number.
To state the product of prime factors of 54, you use a factor tree:
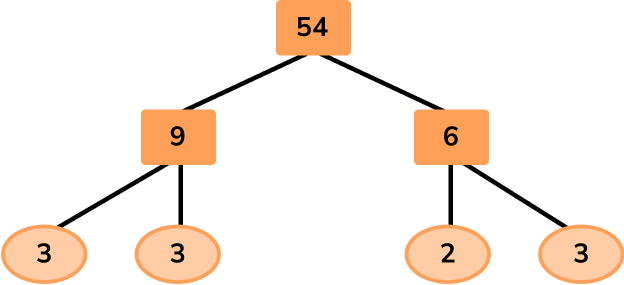
\begin{aligned} & 54=2 \times 3 \times 3 \times 3 \\\\
& 90=2 \times 3 \times 3 \times 5 \end{aligned}
Write all the prime factors into the Venn diagram for each number.
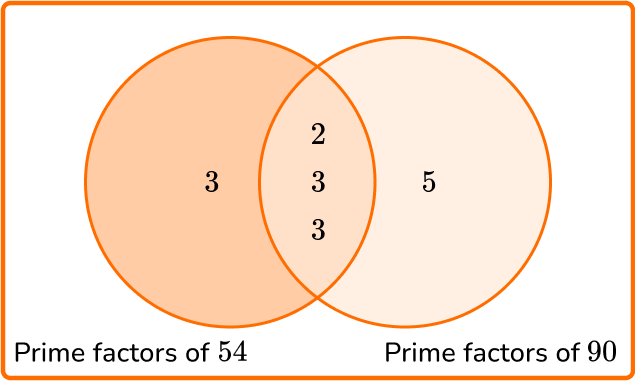
Multiply each prime factor in the Venn diagram to find the LCM.
LCM =3 \times 2 \times 3 \times 3 \times 5=270
Example 4: three composite numbers
Calculate the least common multiple of 12, 20, and 32.
State the product of prime factors of each number.
\begin{aligned} & 12=2 \times 2 \times 3 \\\\ & 20=2 \times 2 \times 5 \\\\ & 32=2 \times 2 \times 2 \times 2 \times 2 \end{aligned}
Write all the prime factors into the Venn diagram for each number.
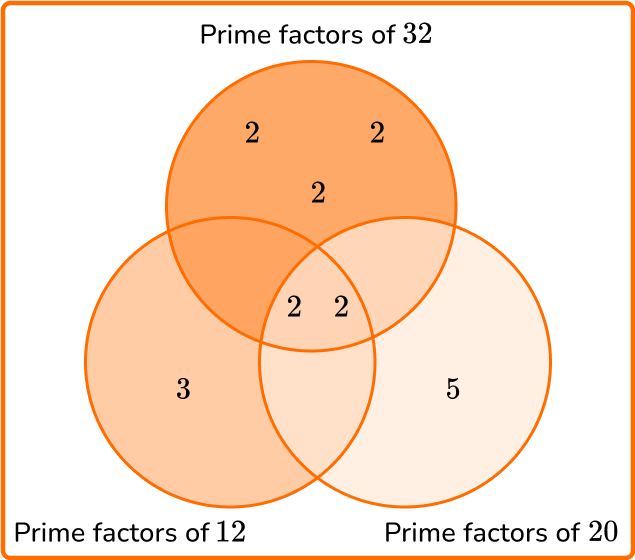
Multiply each prime factor in the Venn diagram to find the LCM.
LCM =2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 5=480
Example 5: the least common multiple = a × b
Calculate the least common multiple of 35 and 72.
State the product of prime factors of each number.
\begin{aligned} & 35=5 \times 7 \\\\ & 72=2 \times 2 \times 2 \times 3 \times 3 \end{aligned}
Write all the prime factors into the Venn diagram for each number.
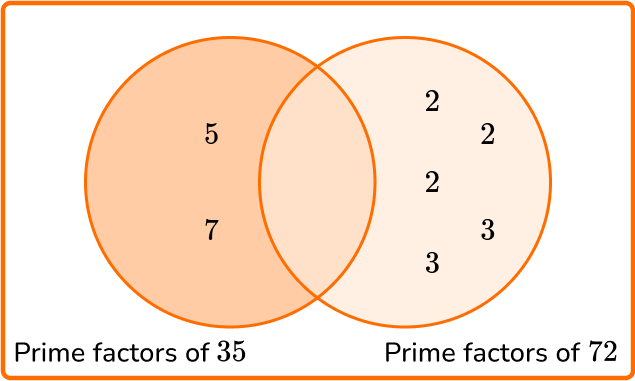
Multiply each prime factor in the Venn diagram to find the LCM.
LCM =5 \times 7 \times 2 \times 2 \times 2 \times 3 \times 3=35 \times 72=2,520
Example 6: word problem
There are two lights blinking on a machine. The green light blinks every 36 seconds and the blue light blinks every 42 seconds. When they both blink at the same time, how much time is it before they blink at the same time again?
State the product of prime factors of each number.
\begin{aligned} & 36=2 \times 2 \times 3 \times 3 \\\\ & 42=2 \times 3 \times 7 \end{aligned}
Write all the prime factors into the Venn diagram for each number.
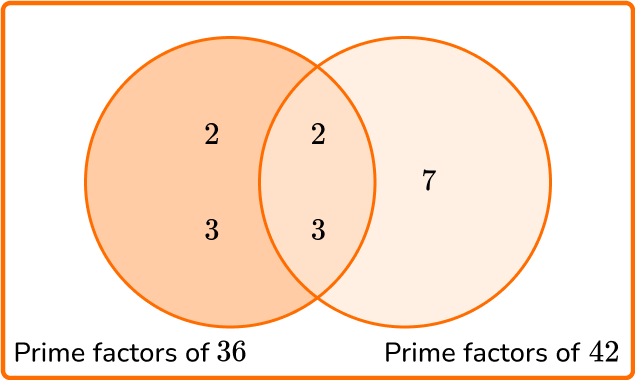
Multiply each prime factor in the Venn diagram to find the LCM.
LCM =2 \times 3 \times 2 \times 3 \times 7=252 seconds
To answer the question:
252 seconds = 4 minutes and 12 seconds, so they blink at the same time every 4 minutes and 12 seconds.
Teaching tips for least common multiple
- At the beginning, use smaller numbers so students can focus on learning and understanding the procedure. Then move to larger numbers to challenge students’ ability to find all the prime factors of a number.
- Look for opportunities for students to use LCM in real-world situations instead of using just practice problem worksheets.
- Some students may struggle to find all the prime factors, especially for larger numbers. Provide a calculator to assist students so that they can keep their focus on the skill and not be held back by the calculations.
Easy mistakes to make
- Calculating the greatest common factor (GCF) instead of LCM
It is common to mix up the least common multiple with the greatest common factor. To avoid this, remember the definition of multiples and factors.
Multiples: the product of two or more factors being multiplied
Factors: the number being multiplied
For example,
What is the GCF of 3 and 9? What is the LCM of 3 and 9?
Factors of 3\text{: } 1, 3 Multiples of 3\text{: } 3, 6, 9, 12, 15…
Factors of 9\text{: } 1, 3, 9 Multiples of 9\text{: } 9, 18, 27, 36…
The GCF is 3 The LCM is 9
- Multiplying the two numbers and assuming that is the LCM
Multiplying the two numbers in the question will find a common multiple, but it may not be the least common multiple.
For example,
What is the LCM of 3 and 9?
3 \times 9 = 27 ← common multiple, but not the LCM
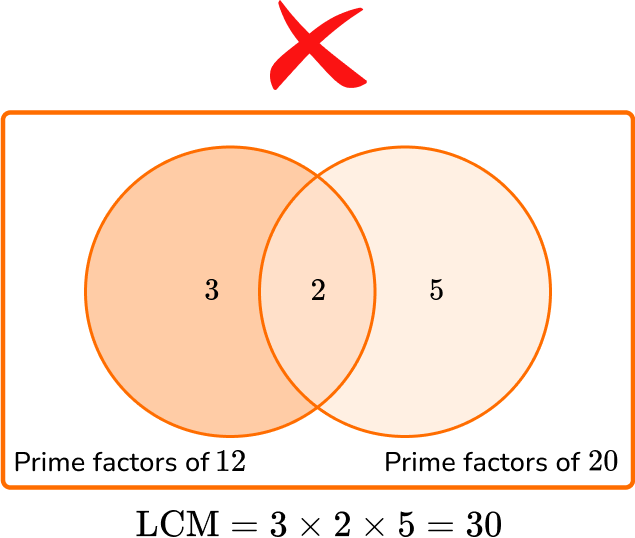
- Not writing duplicate factors in the Venn diagram
It is easy to forget the repeated prime factors in a Venn diagram, but the procedure only works if they are all included.
For example,
What is the LCM of 12 and 20?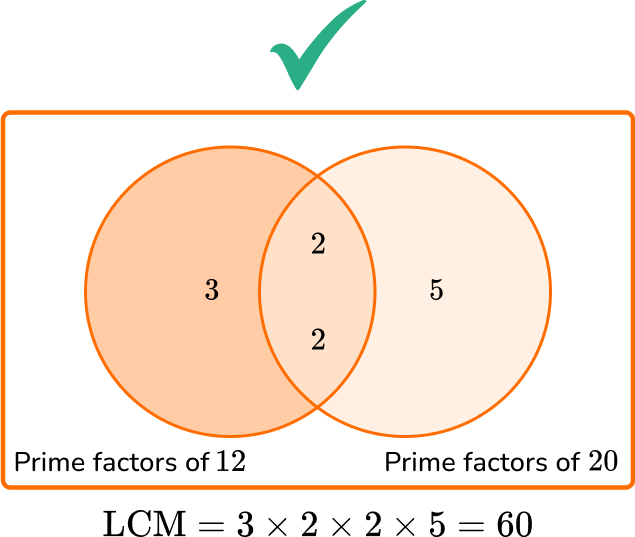
Related lessons on factors and multiples
Least common multiple practice questions
1. Calculate the least common multiple of 42 and 70.




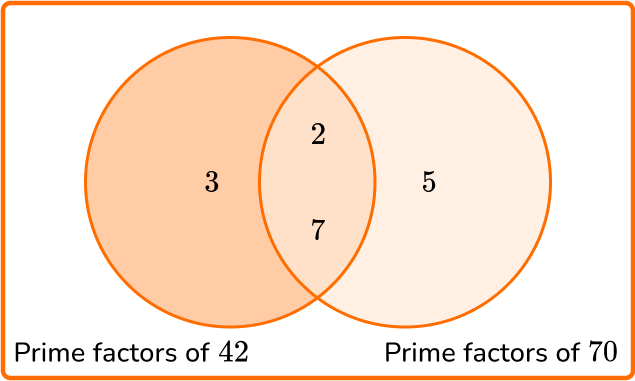
LCM =2\times 3 \times 5 \times 7=210
2. Calculate the least common multiple of 38 and 76.




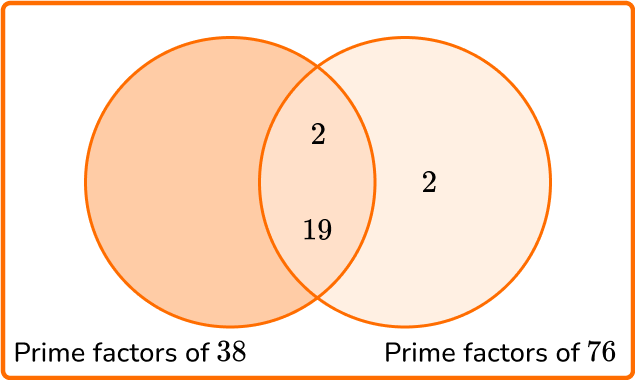
LCM =2 \times 2 \times 19 =76
3. Given that 68=2^{2} \times 17, calculate the least common multiple of 24 and 68.




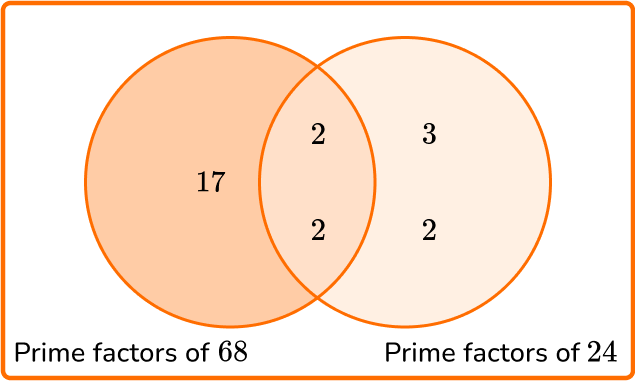
LCM =2 \times 2 \times 2 \times 3 \times 17=408
4. Calculate the least common multiple of 10, 25, and 45.




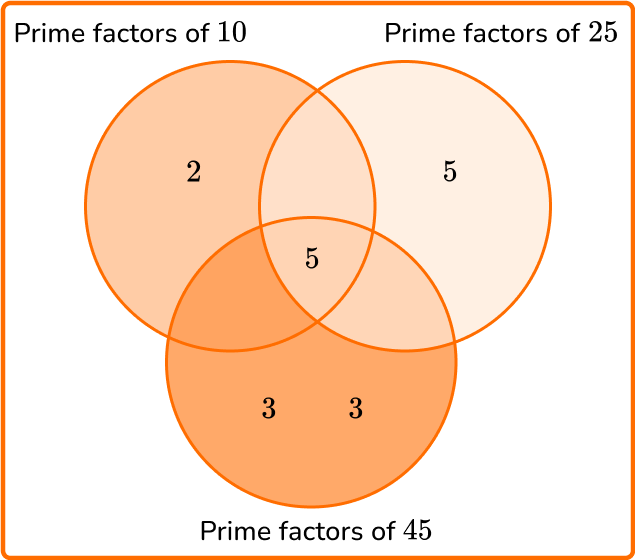
LCM =2 \times 3 \times 3 \times 5 \times 5 = 450
5. Calculate the least common multiple of 16 and 45.




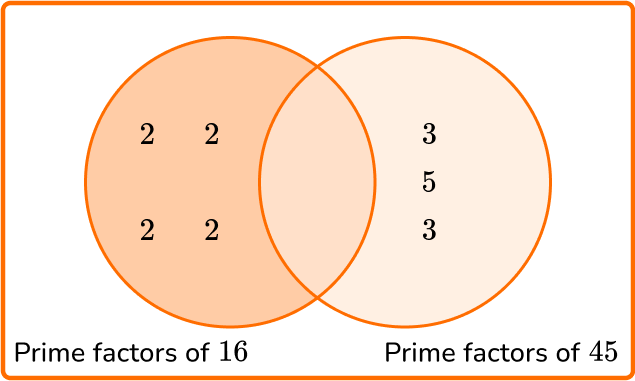
LCM =2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 5 =720
6. Two buckets of water are leaking. Bucket A drips water every 16 seconds, while bucket B drips water every 18 seconds. If they both drip water at the same time, what is the length of time between them both dripping water again at the same time?
144 mins

2 secs

1 min 12 secs

2 mins 24 secs

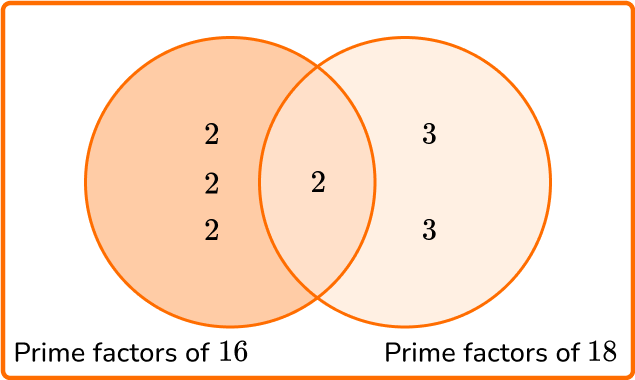
LCM =2 \times 2 \times 2 \times 2 \times 3 \times 3=144
144 seconds = 2 mins 24 secs
Least common multiple FAQs
The Venn diagram breaks each number down into its prime factors. Writing numbers once in the intersection eliminates all the duplicate factors, so what is left are the prime factors of the smallest multiple the numbers have in common. So multiplying them together equals the LCM.
Lowest Common Denominator (LCD), Least Common Denominator (LCD), and Lowest Common Multiple (LCM) are also other terms that mean the same as Least Common Multiple.
Yes, besides the prime factorization method, you can make a list of multiples for each number until you reach the first common multiple.
No, not necessarily. For example, the number 36=2 \times 2 \times 3 \times 3 has 4 prime factors while 71 = 3 \times 17 has only 2, so in this case the smallest number has more factors.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!