High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Addition and subtraction Multiplication and division Decimals Fractions Order of operations Ratios Solving equations SubstitutionFunction machines
Here you will learn about function machines, including finding outputs, finding inputs and using function machines to solve equations.
Students will first learn about function machines as part of functions in 8 th grade.
What is a function machine?
A function machine is used to apply operations in a given order to a value known as the Input. The final value produced is known as the Output. For each input, there is one unique output.
A function machine can be applied to numbers or be used for algebraic manipulation.
For example,
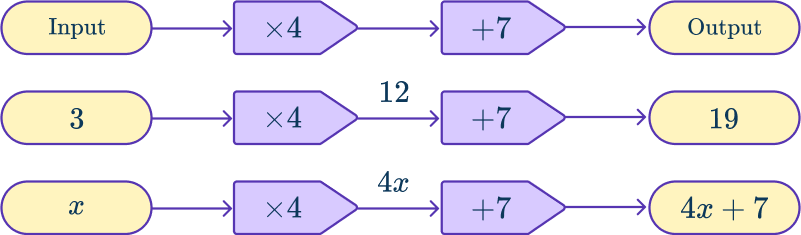
When 3 is substituted for the input, each operation of the function machine is used in order to calculate the output.
When the input is unknown (represent by a variable, like x ), the inverse operations of the function machine are used to work backwards in order to calculate the missing input.
Note: Not all equations can be solved using a function machine, but they can be applied to a lot of situations where the unknown is on one side of the equation.
Function machines can be used to help produce tables of values for graphs such as quadratic or cubic graphs, but this page will only cover linear functions.
What is a function machine?
Common Core State Standards
How does this relate to 8 th grade math?
- Grade 8 – Functions (8.F.A.1)
Understand that a function is a rule that assigns to each input exactly one output. The graph of a function is the set of ordered pairs consisting of an input and the corresponding output.
![[FREE] Function Machine Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/05/Function-Machine-Worksheet-listing-image.png)
[FREE] Function Machine Worksheet (Grade 6 to 8)
![[FREE] Function Machine Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/05/Function-Machine-Worksheet-listing-image.png)
Use this worksheet to check your grade 6 to 8 students’ understanding of function machines. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Function Machine Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/05/Function-Machine-Worksheet-listing-image.png)
[FREE] Function Machine Worksheet (Grade 6 to 8)
![[FREE] Function Machine Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2024/05/Function-Machine-Worksheet-listing-image.png)
Use this worksheet to check your grade 6 to 8 students’ understanding of function machines. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEHow to find the output of a function machine
In order to find the output of a function machine given an input:
- Substitute the given value for the input.
- Follow the steps in the function machine in order to calculate the output.
Solving using function machine examples
Example 1: substitution in a 2 -step function machine

What is the output when the input is 7?
- Substitute the given value for the input.

2Follow the steps in the function machine in order to calculate the output.
First, add 11.
7+11=18Then, multiply by \cfrac{1}{4}.
18\times\cfrac{1}{4}=4\cfrac{1}{2}The output is 4\cfrac{1}{2} or 4.5.
Example 2: substitution in a 2 -step function machine

What is the output when the input is 13?
Substitute the given value for the input.

Follow the steps in the function machine in order to calculate the output.
First, multiply by 5.
13\times{5}=65
Then, subtract 45.6.
65-45.6=19.4
The output is 19.4.
How to solve equations using a function machine
In order to solve a linear equation using a function machine:
- Consider the order of operations being applied to the unknown.
- Draw a function machine starting with the unknown as the Input and the value the equation is equal to as the Output.
- Work backwards, applying inverse operations to find the unknown Input.
Example 3: solving a one step equation using a function machine
Solve 4x=- \, 5.
Consider the order of operations being applied to the unknown.
The only operation is \times \, 4.
Draw a function machine starting with the unknown as the Input and the value the equation is equal to as the Output.
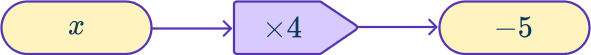
Work backwards, applying inverse operations to find the unknown Input.
Example 4: solving a two step equation using a function machine
Solve \cfrac{x}{2}-6=3 .
Consider the order of operations being applied to the unknown.
The order of operations is \div \, 2, then - \, 6.
Draw a function machine starting with the unknown as the Input and the value the equation is equal to as the Output.

Work backwards, applying inverse operations to find the unknown Input.
Example 5: solving a two step equation using a function machine
Solve 5.8(x+2)=24.36 .
Consider the order of operations being applied to the unknown.
The order of operations is + \, 2, then \times \, 5.8
Draw a function machine starting with the unknown as the Input and the value the equation is equal to as the Output.

Work backwards, applying inverse operations to find the unknown Input.
Example 6: solving a three step equation using a function machine
Solve \cfrac{3p-1}{4}=8 .
Consider the order of operations being applied to the unknown.
The order of operations is \times \, 3, then - \, 1, then \div \, 4.
Draw a function machine starting with the unknown as the Input and the value the equation is equal to as the Output.
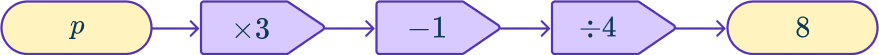
Work backwards, applying inverse operations to find the unknown Input.
Teaching tips for function machine
- Review the concept of functions and input-output tables before teaching students how to use a function machine.
- Use printable, function machine worksheets that have a variety of representations, like algebraic expressions, function tables and graphs.
- For English language learners or other learners who are unsure why these are referred to as “machines,” utilize an interactive, free resource that shows the “action” of the machine changing from input to output.
- Decide where this topic best fits within your state’s interpretation of CCSS-M, before introducing function machines.
Easy mistakes to make
- Not working backwards when using inverse functions
When a function rule has two or more steps, a common error is to forget to work backwards. The inverse operations are used but in the wrong order.
For example,
Solving the function below as 3\times{2}+6, instead of (3+6)\times{2}.
- Not using the correct order of operations when drawing a function machine
When creating a function machine, follow the correct order of operations for an equation.
For example,
In the equation 1+2x=7, the multiplication by two takes place before subtracting one.
Related what is a function lessons
Practice function machine questions
1. What is the output when the input is 9?
![]()




Substitute 9 as the input and solve.
![]()
(9-7)\div\cfrac{1}{2}=2\div\cfrac{1}{2}=4
2. Select the correct function machine for the equation:
5x=10
![]()

![]()

![]()

![]()

x is the input, the operation is multiplying by 5, the output is 10.
3. Select the correct function machine for the equation:
2x-6=10
![]()

![]()

![]()

![]()

x is the input, the first operation is multiplying by 2, the second operation is subtracting 6, the output is 10.
4. Find the missing input for the function machine.
![]()




Work backwards, using inverse operations, to find n.
(8+4)\times{7}=84
5. Find the missing input for the function machine.
![]()




Work backwards, using inverse operations, to find q.
(14\times{3}-2)\div{5}=8
6. Find the missing output and missing input for the function machine.





Work forwards to find a.
(5\times{3})+2=17
Work backwards, using inverse operations, to find b.
(11-2)\div{3}=3
Function machine FAQs
A number machine is an alternative name for function machines. A number machine is a way of writing the rules which link the inputs and the outputs.
Yes, function machines can be used to model any type of equation that is a function. These more complex functions are typically introduced in high school.
The next lessons are
- Law of exponents
- Scientific notation
- Quadratic graphs
- Function notation
- Composite functions
- Inverse functions
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!