2. Which is an example of a function?

4. Select the correct function machine and solution for the equation: $ 2x+6=10 $

5. If $ g(x)=0.4^x, $ which graph shows function $ g? $

What is a Function - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Number patterns Input/output tables Coordinate plane Types of graphs

Math resources Algebra

What is a function

Here you will learn about functions in algebra, including what functions are, how to calculate with function machines and exponential functions.

Students will first learn what is a function as part of functions in $8$ th grade and continue to learn about them in high school.

What is a function?

A function has the relationship where there is one unique output for each input.

A function can be represented by a…

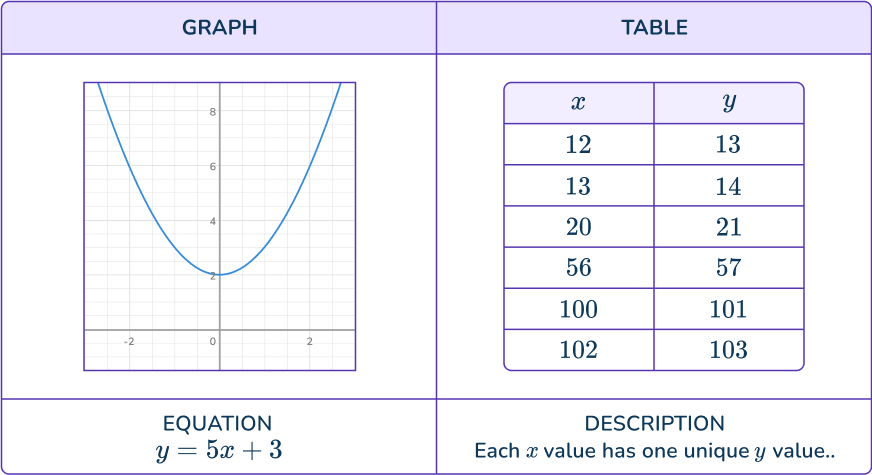
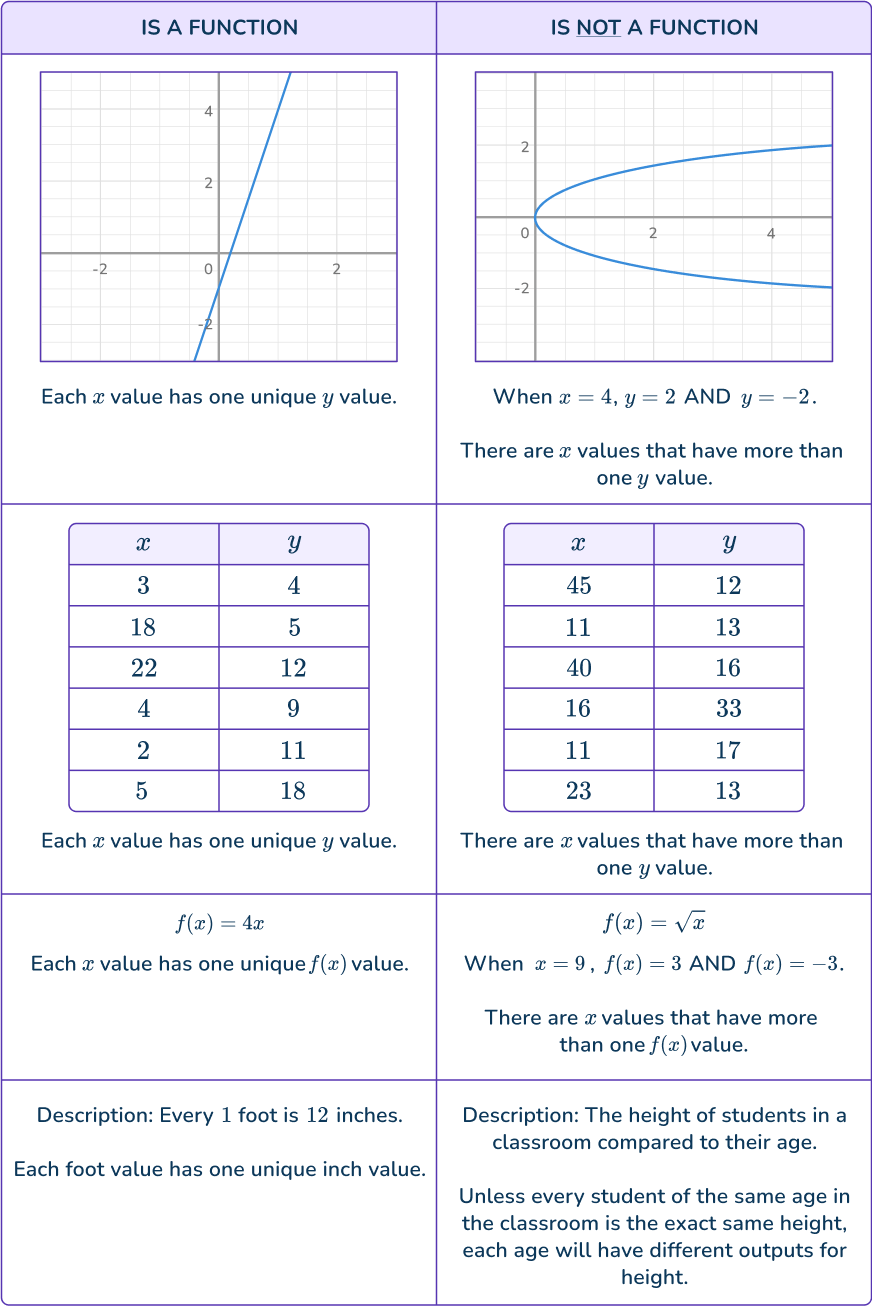
Let’s look at another example and a non-example of each type.

For example,

Functions in algebra are used to describe the operation being applied to an input in order to get an output.

[FREE] Algebra Worksheet (Grade 6 to 8)

Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th and 8th grade algebra topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Algebra Worksheet (Grade 6 to 8)

DOWNLOAD FREE

Function machines

Functions can be presented using a function machine.

Step-by-step guide: Function machine

Function notation

Functions can be described using function notation.

The $f$ in $f(x)$ is known as the function that is being applied to a variable $x.$ Other letters such as $g$ and $h$ are also commonly used.

For example,

Let’s look at a function $f$ described by a function machine:

Then let’s rewrite this using function notation:

An exponential function is in the form $y=ab^x,$ and is a mathematical function where $x$ and $y$ are variables, and $a$ and $b$ are constants, $b>0.$

For example,

The diagram shows the graphs of $y=2^x, y=0.4^x$ and $y=0.5(3^x).$

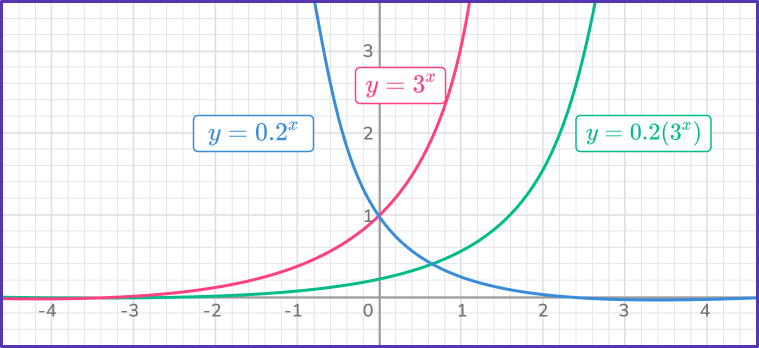
The domain of the functions is all real numbers. Let’s consider the range of the functions. It may appear that the functions reach the $y$ -axis on the graph of the functions, but they do not.

They are actually continually getting closer and closer to the $y$ -axis, but will never intersect. This is a horizontal asymptote at $y=0$ (the $x$ -axis) and it occurs because $a b^x$ can never equal zero.

What is a function?

Common Core State Standards

How does this relate to $8$ th grade math and high school math?

Grade 8 – Functions (8.F.A.1)
Understand that a function is a rule that assigns to each input exactly one output. The graph of a function is the set of ordered pairs consisting of an input and the corresponding output.

Functions – Interpreting Functions (HSF.IF.C.7e)
Graph exponential and logarithmic functions, showing intercepts and end behavior, and trigonometric functions, showing period, midline, and amplitude.

Functions – Linear, Quadratic and Exponential Models (HSF.LE.A.2)
Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (including reading these from a table).

How to decide what is a function

In order to decide what is a function:

Decide if each input $\textbf{(x)}$ has ONE unique output $\textbf{(y)}$ .
If so, it is a function. If not, it is not a function.

What is a function examples

Example 1: is the graph a function?

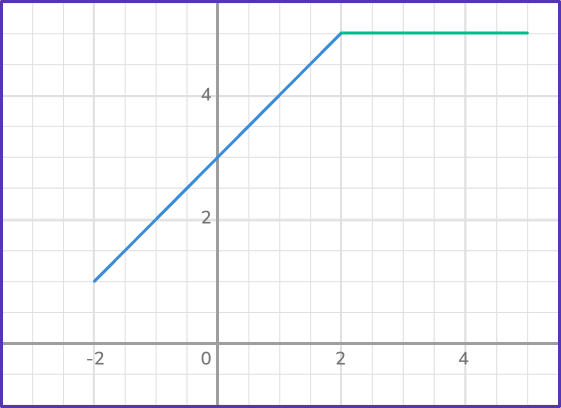
Is the graph a function?

Decide if each input $\textbf{(x)}$ has ONE unique output $\textbf{(y)}$ .

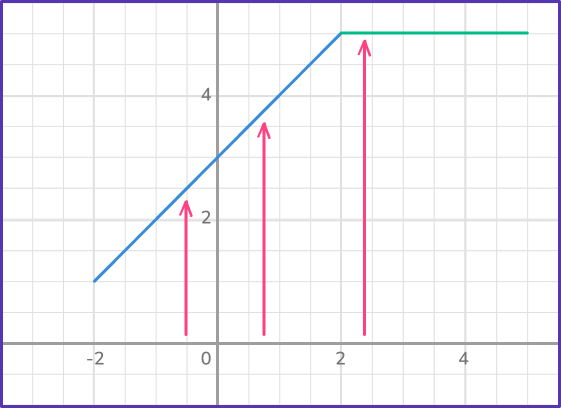
All inputs ( $x$ values) correspond to only one point on the line – one output ( $y$ value).

2If so, it is a function. If not, it is not a function.

The graph IS a function.

Example 2: is the table a function?

Is the table a function?

Decide if each input $\textbf{(x)}$ has ONE unique output $\textbf{(y)}$ .

All inputs ( $x$ values) correspond to only one point on the line – one output ( $y$ value).

If so, it is a function. If not, it is not a function.

The table IS a function.

Note: Both inputs $5$ and $7$ map to $2.$ This is fine. Each output does NOT need a unique input to be a function.

How to use function machines

In order to solve an equation using a function machine:

Consider the order of operations being applied to the unknown.
Draw a function machine starting with the unknown as the Input and the value of the equation as the Output.
Work backwards, applying inverse operations to find the unknown Input.

Function machines example

Example 3: solving a one step equation using a function machine

Solve $x+5=12$ .

Consider the order of operations being applied to the unknown.

The only operation is $+ \, 5.$

Draw a function machine starting with the unknown as the Input and the value the equation is equal to as the Output.

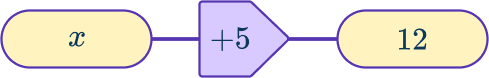
Work backwards, applying inverse operations to find the unknown Input.

\begin{aligned}& x=12-5 \\\\ & x=7 \end{aligned}

Example 4: solving a two step equation using a function machine

Solve $\cfrac{x}{3}+7=3$ .

Consider the order of operations being applied to the unknown.

The order of operations is $\div 3,$ then $+ \, 7.$

Draw a function machine starting with the unknown as the Input and the value of the equation as the Output.

Work backward, applying inverse operations to find the unknown Input.

\begin{aligned}& x=\left( 3-7 \right)\times 3 \\\\ & x=- \, 12 \end{aligned}

How to find the equation of exponential functions

In order to find the equation of exponential functions:

Find two points that lie on the graph.
Form two equations in the form $\bf{\textbf{y}=\textbf{ab}^\textbf{x}}.$
Solve the equations simultaneously.

Step-by-step guide: Exponential function

Example 5: finding exponential functions given the y-intercept

Find the equation of the exponential function in the form $y=ab^x.$

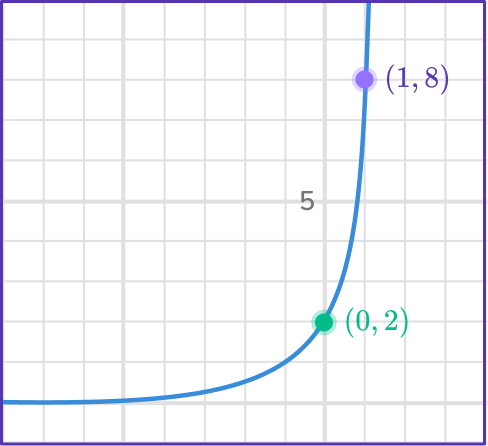
Find two points that lie on the graph.

You have the points $(0, 2)$ and $(1, 8).$

Form two equations in the form $\bf{\textbf{y}=\textbf{ab}^\textbf{x}}.$

$(0, 2)$ gives us $2=ab^0.$

$(1, 8)$ gives us $8=ab^1.$

Solve the equations simultaneously.

You can simplify the two equations before solving.

$b^0=1,$ therefore

$2=ab^0$ gives us $a=2.$

$b^1=b,$ therefore

$8=ab^1$ gives us $8=ab.$

You know $a=2,$ therefore,

\begin{aligned}& 8=2 b \\\\ & b=4 \end{aligned}

The exponential equation is $y=2(4^x).$

Example 6: finding exponential functions by dividing the equations

Find the equation of the exponential function in the form $y=ab^x.$

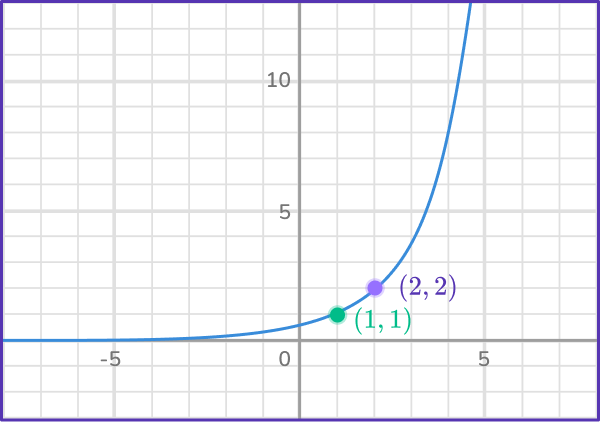
Find two points that lie on the graph.

You have the points $(1, 1)$ and $(2, 2).$

Form two equations in the form $\bf{\textbf{y}=\textbf{ab}^\textbf{x}}.$

$(1, 1)$ gives us $1=ab.$

$(2, 2)$ gives us $2=ab^2.$

Solve the equations simultaneously.

You can solve the equations simultaneously by dividing one equation by the other.

$\cfrac{2}{1}=\cfrac{a b^2}{a b}$

This gives $2=b.$

Substituting this into $1=ab$ gives

\begin{aligned}& 1=2 a \\\\ & a=0.5 \end{aligned}

The exponential equation is $y=0.5\left(2^x\right).$

Example 7: finding exponential functions by dividing the equations

Find the equation of the exponential function in the form $y=ab^x.$

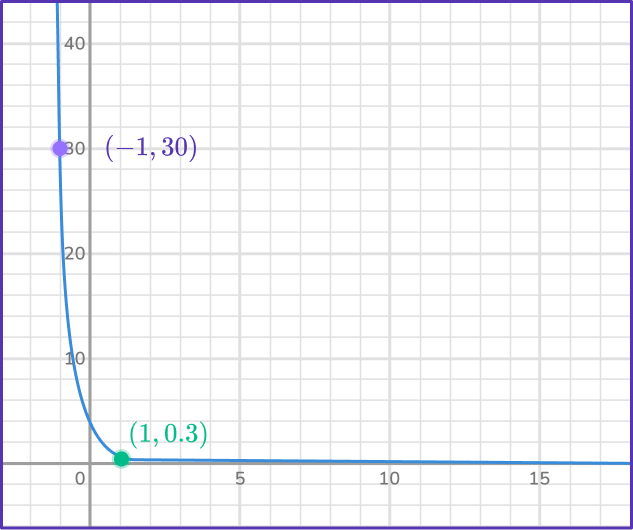
Find two points that lie on the graph.

You have the points $(- \, 1, 30)$ and $(1, 0.3).$

Form two equations in the form $\bf{\textbf{y}=\textbf{ab}^\textbf{x}}.$

$(- \, 1, 30)$ gives us $30=ab^{-1}.$

$(1, 0.3)$ gives us $0.3=ab^{1}.$

Solve the equations simultaneously.

You can solve the equations simultaneously by dividing one equation by the other.

$\cfrac{0.3}{30}=\cfrac{a b^1}{a b^{-1}}$

This gives

$0.01=b^2$

$0.1=b$

Substituting this into $0.3=a b^1$ gives

\begin{aligned}& 0.3=0.1 a \\\\ & a=3\end{aligned}

The exponential equation is $y=3(0.1^x).$

Teaching tips for what is a function

When first teaching functions, focus on identifying whether or not something is a function and not necessarily identifying the function name (type of function).

Expose students to more than just linear functions, by including a variety of other types, such as quadratic, exponential or polynomial functions.

Represent functions and non-functions in a variety of ways. While students may find the vertical line test useful, ensure that this is not the only way they can identify a function.

Let struggling students use calculators, so the focus is on the function and not the calculations.

Easy mistakes to make

Thinking only graphs or equations are functions
While these are common ways to represent functions, it is important to know that functions can also be represented by tables or descriptions.
For example,

Description: The input, $x,$ cubed is equal to the output, $y.$
The table and description represent a function since each input has one unique output.

Thinking every function must have an equation
Many functions can be represented by an equal, but this is not a requirement.
Some functions cannot be represented by an equation.
For example,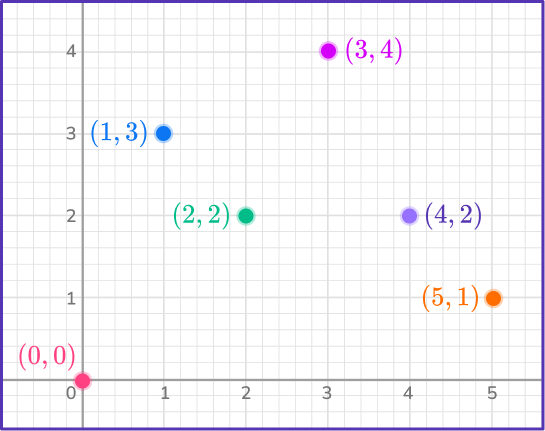

The graph represents a function since each input has one unique output, but no equation fits this function.

Thinking $\textbf{y}$ values can’t repeat for different $\textbf{x}$ values
The domain of a function is the $x$ values and they must each have a unique output. However, the range of a function, the $y$ values, may repeat.

In the graph of the function above, notice that $y=2$ for both $x=2$ and $x=4.$

Students who think the input values or output values are always all real numbers
Sometimes the input and output value are all real numbers, but this is not always the case. Either the domain or range or both can be a subset, such as just integers or whole numbers. This is why it is important to always define the domain and range of a function.

Not using the correct order of operations when drawing a function machine
A common error is to not follow the correct order of operations when creating a function machine for an equation.

For example, for the equation $2 x-1=7,$ the multiplication by two takes place before subtracting one.

Function notation is mistaken for a product
It is common for $f(x)$ to be thought of as $“f$ times $x$ rather than $“f$ of $x”.$ This confusion can lead to incorrect evaluations of values.

For example,
When finding $f(2)$ when $f(x)=x+3,$ a student may think $f(2)$ means $2(x+3).$

The correct solution is,
$\begin{aligned}&f(x)=x+3 \\\\ &f(2)=2+3 \\\\ &f(2)=5 \end{aligned}$

Incorrectly applying the exponent to both variables
It is easy to assume that $y=ab^x$ with $y=(ab)^x$ are equal. However, $y=ab^x$ means $y=a \times\left(b^x\right)$ and this means $y=(ab)^x$ , which is a different function.

Practice what is a function questions

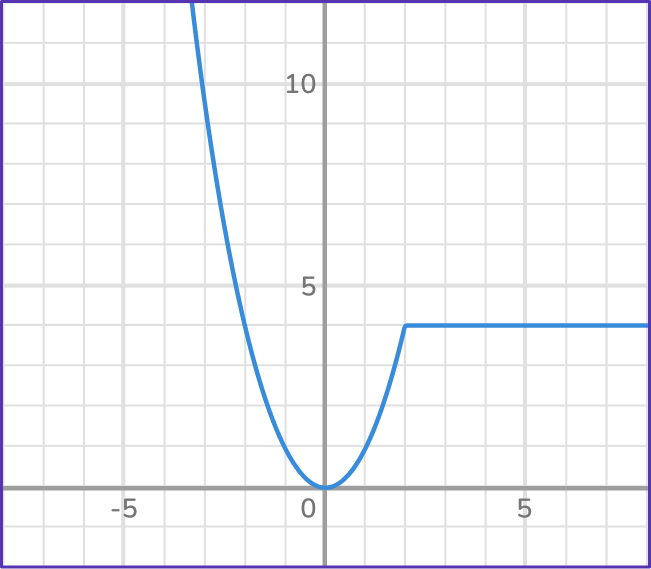
Yes, because each output has a unique input.

Yes, because each input has a unique output.

No, because each output does NOT have a unique input.

No, because each input does NOT have a unique output.

A function has a unique output for each input.

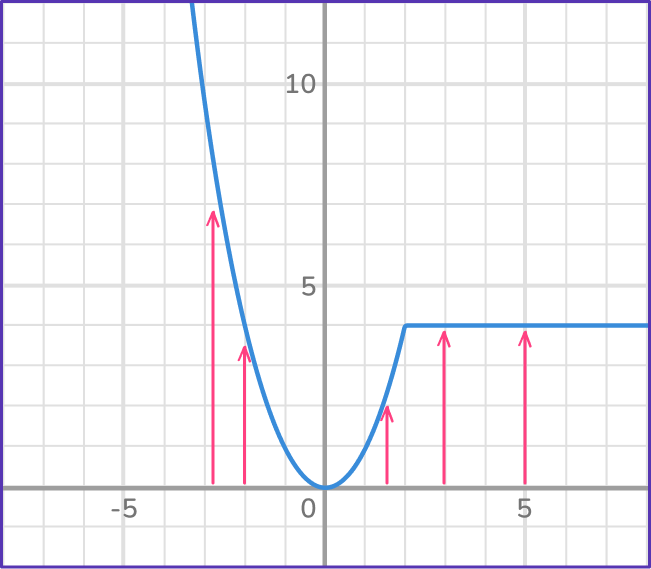
What is a function image 18 US

In the graph, no matter which input value, $x,$ you choose, it will have a unique output. Therefore the graph IS a function.

What is a function image 19 US

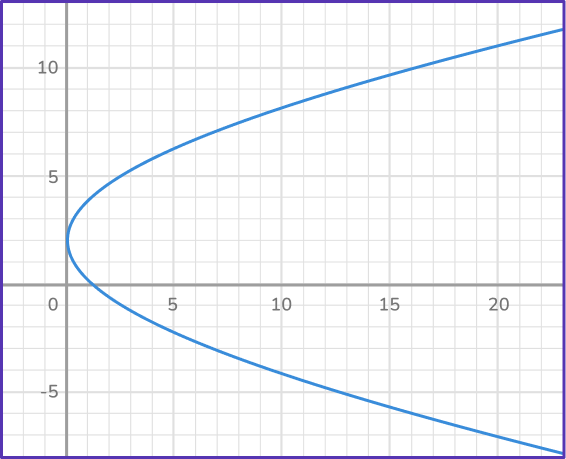
What is a function image 20 US

What is a function image 21 US

What is a function image 22 US

A function has a unique output for each input.

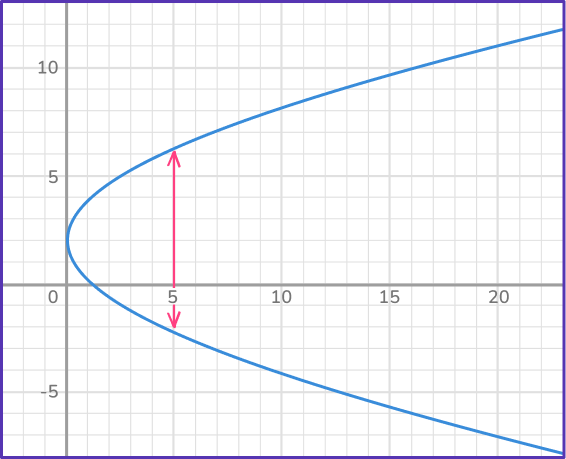
What is a function image 23 US

$x=5$ has two outputs. The graph is NOT a function.

What is a function image 24 US

$x=5$ has two outputs. The table is NOT a function.

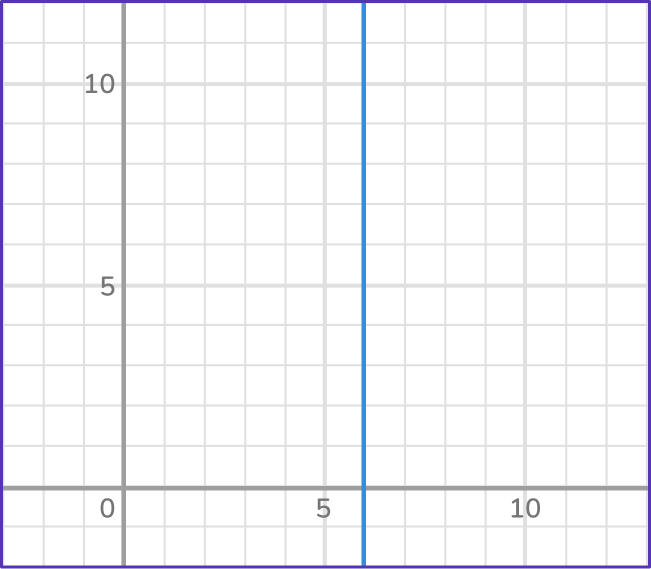
What is a function image 25 US

$x=6$ has many outputs. The table is NOT a function.

Each input in the table has a unique output.

What is a function image 26 US

This table is a function.

a=21, b=2.5

a=12, b=25

a=21, b=16

a=4.5, b=40

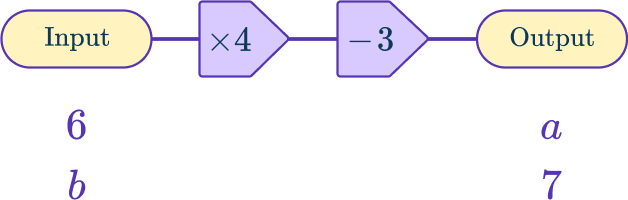
Work forwards to find $a$ by starting with $6$ and using the rules

6 \times 4-3=21

Work backwards to find $b$ by starting $7$ and using the opposite of the rules.

(7+3) \div 4=2.5

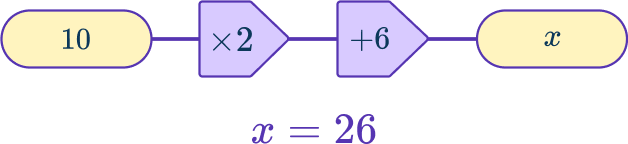
What is a function image 28 US

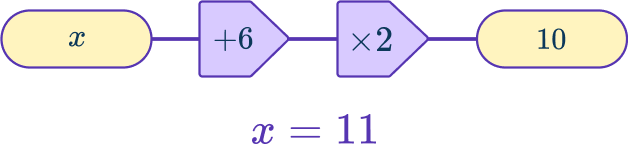
What is a function image 29 US

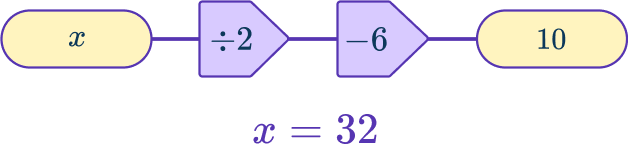
What is a function image 30 US

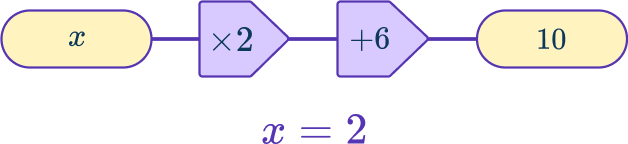
What is a function image 31 US

In $2x+6=10, \, x$ is the input and the first operation is multiplying by $2.$

This represents $2x.$

The second operation is adding $6,$ the output is $10.$

This represents $+ \, 6=10.$

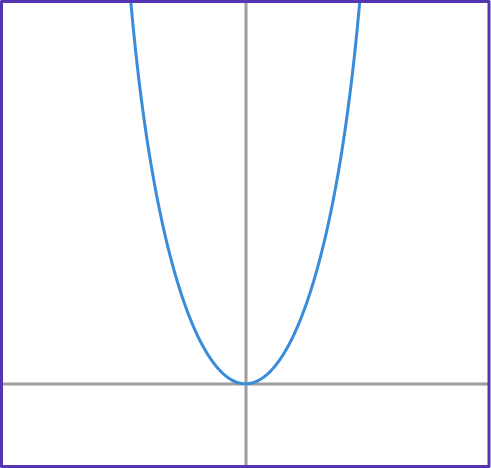
What is a function image 34 US

What is a function image 35 US

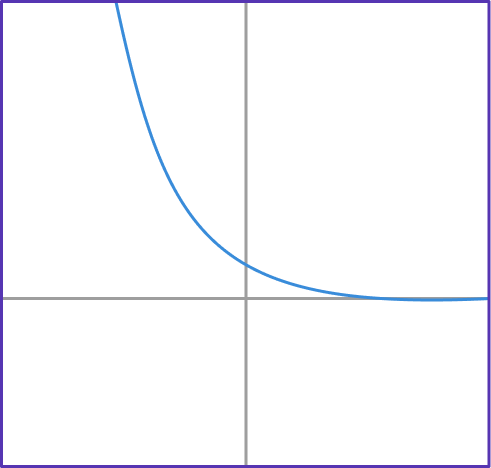
What is a function image 36 US

What is a function image 37 US

$g(x)=0.4^x$ has the table of values shown below.

What is a function image 38 US

Notice that the $g(x)$ values are decreasing exponentially. This table of values matches the form of the graph…

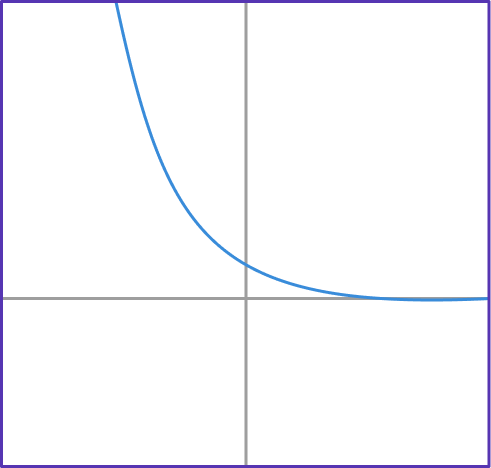
What is a function image 39 US

y=2.5(6^x)

y=1.5(6^x)

y=6(2.5^x)

y=6(1.5^x)

Using the points and $y=ab^x, \, b>0.$

$(1, 4)$ gives $4=ab.$

$(5, 1.6384)$ gives $1.6384=ab^5$

Dividing gives

\begin{aligned}& \cfrac{1.6384}{4}=\cfrac{a b^5}{a b} \\\\ & 0.4096=b^4 \\\\ & b=0.8\end{aligned}

Substituting into $4=ab$ gives $a=5.$

What is a function FAQs

What is the definition of a function?

A relationship where every input has one unique output.

What are examples of other types of functions not shown in this page?

There are many types of functions, including quadratic functions, trigonometric functions (sine, cosine, tangent), square root functions, inverse functions, composite functions and more.

What is a one-to-one function?

A function where all $y$ values are unique to one $x$ value.

What is the codomain?

It is the output value(s) of a function. Also known as the ‘range.’

What are the independent variables and dependent variables?

The input values are known as independent variables and the output values are known as dependent variables.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.