High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Order of operationsOne-step equations
Solving equations Algebraic expressions Simplifying expressions
Factoring out the
Literal equations
Here you will learn about what a literal equation is, how to solve for a specific variable in a literal equation, and how to use a literal equation to problem solve.
Students first learn about literal equations in algebra 1 and expand that knowledge as they progress through high school mathematics.
What is a literal equation?
Literal equations are equations that have more than one variable in them. Literal equations are represented by formulas and equations. Here are some examples of literal equations.

Notice how the formulas all have more than one variable in them. To solve a literal equation, it essentially means to rearrange the formula or equation to isolate one of the variables.
The steps taken to solve a literal equation are the same as those applied to solving a regular multi-step equation that has one unknown variable and numerical values.
When solving equations, the inverse operation(s) are applied to the equation. When solving literal equations, the inverse operation needs to be applied in order to solve.
Recall the order of operations and their inverses:
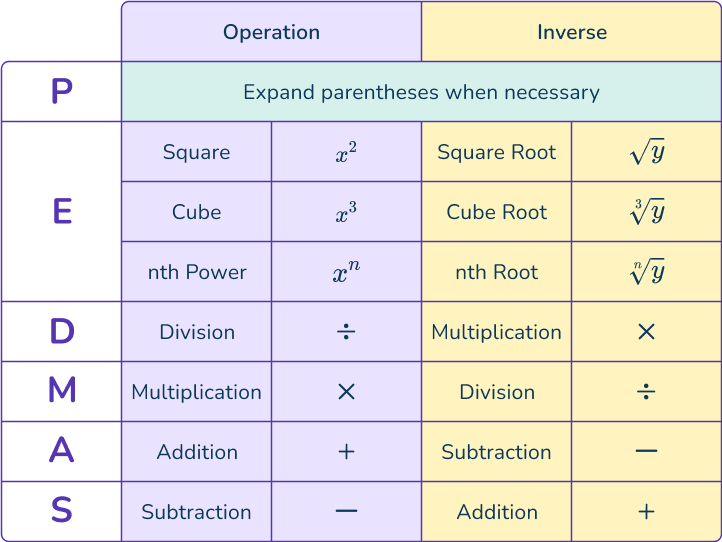
Solving a literal equation for a specific variable is also known as changing the subject of the formula or equation.
Let’s look at a side-by-side comparison of solving algebraic equations and literal equations to make important connections.

What is a literal equation?

Common Core State Standards
How does this apply to high school math?
- High School Algebra – Creating Equations (HSA-CED.A.4)
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations. For example, rearrange Ohm’s law V=IR to highlight resistance R.
- High School Algebra – Reasoning with Equations and Inequalities (HSA-REI.B.3)
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Algebra Worksheet (Grade 6 to 8)
![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th and 8th grade algebra topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
[FREE] Algebra Worksheet (Grade 6 to 8)
![[FREE] Algebra Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Algebra-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th and 8th grade algebra topics to identify areas of strength and support!
DOWNLOAD FREEHow to solve literal equations
In order to solve literal equations:
- Use inverse operations to move a number, term, or variable.
- Repeat this process until the remaining variable is the subject.
- Write the answer.
Solving literal equations examples
Example 1: solve the formula for a variable
Use the distance formula to solve for t.
d=rt- Use inverse operations to move a number, term, or variable.
To solve for t move the r to the other side of the equation by doing the inverse operation, which is to divide.
\begin{aligned}\cfrac{d}{r}&=\cfrac{rt}{r} \\\\ \cfrac{d}{r}&=t \end{aligned}2Repeat this process until the remaining variable is isolated.
The t is isolated so no need to do the process again.
3Write the answer.
\cfrac{d}{r}=tOR
t=\cfrac{d}{r}Example 2: solve a linear equation for y
Solve the linear equation for y.
2x+3y=12Use inverse operations to move a number, term, or variable.
Move the 2x first by doing the inverse operation, which is to subtract 2x from both sides of the equation.
Repeat this process until the remaining variable is isolated.
The y is still not isolated.
3y=12-2x
Move the 3 to the other side of the equation by doing the inverse operation, which is to divide by 3.
Write the answer.
You can also express the answer by dividing both 12 and 2x by 3.
y=4-\cfrac{2}{3}x
See also: Linear equations
Example 3: volume formula
Use the formula for volume of a cylinder to solve for h.
V=\Pi{r^2}hUse inverse operations to move a number, term, or variable.
To isolate the h, move the \Pi by doing the inverse operation, which is to divide.
Repeat this process until the remaining variable is isolated.
The h is still not isolated, move the r^2 by doing the inverse operation which is division or multiply by the reciprocal.
This can be simplified by multiplying by the reciprocal.
\cfrac{V}{\Pi}\times\cfrac{1}{r^2}=h
Write the answer.
OR
h=\cfrac{V}{r^2 \Pi}
See also: Volume of a cylinder
Example 4: literal equation with a fraction
Solve the given equation for x.
A=\cfrac{x+y}{b}Use inverse operations to move a number, term, or variable.
To solve the equation for x, first move the b by doing the inverse operation, which is to multiply by b.
Repeat this process until the remaining variable is the subject.
The x is still not isolated. Move the y by doing the inverse operation, which is to subtract y.
Write the answer.
OR
x=Ab-y
Example 5: literal equation with parentheses
Solve the equation for x.
2(x+3 y)=15Use inverse operations to move a number, term, or variable.
To start, move the 2 by doing the inverse operation, which in this case is to divide by 2.
Repeat this process until the remaining variable is the subject.
The x is still not isolated, so the next step is to move the 3y by doing the inverse operation, which in this case is to subtract 3y.
Write the answer.
OR
x=7\cfrac{1}{2}-3y
Note: An alternative strategy to solving the equation for x is to distribute the 2 and then use inverse operations.
Example 6: literal equation with fractions
Given the equation \cfrac{a}{b}+\cfrac{c}{d}=e, solve it for a.
Use inverse operations to move a number, term, or variable.
The first step is to move the fraction, \cfrac{c}{d} by doing the inverse operation, which in this case is to subtract \cfrac{c}{d}.
Repeat this process until the remaining variable is the subject.
The a is still not isolated. Move the b by doing the inverse operation which in this case is to multiply.
Write the answer.
OR
a=be-\cfrac{bc}{d}
Teaching tips for solving literal equations
- Have students make comparisons between the strategies used for solving equations and apply them to literal equations. Also, have students circle or highlight the indicated variable that needs to be isolated to help them make visual connections.
- In order for students to practice problems, have them gameplay using digital platforms or participate in scavenger hunts instead of assigning worksheets.
- Incorporate activities such as having students create and solve their own literal equations.
Easy mistakes to make
- Applying the inverse operations incorrectly
The inverse operation used is incorrect. For example, let M=DV. Here, the formula is rearranged to get M-V=D and so the value of V has been subtracted, rather than divided. The correct answer should be \cfrac{M}{V}=D.
- Moving the variables incorrectly
Letters are simply moved from one side of the equals sign to the other. For example, A=lw becomes Al=w which is incorrect. Instead, you need to use the inverse operation which is to divide by l, to the right side and left side of the equation to get w=\cfrac{A}{l}.
- Not multiplying or dividing throughout
When given the equation y=mx+c, if you divide both sides of the equation by m we should get \cfrac{y}{m}=x+\cfrac{c}{m} whereas students would incorrectly write \cfrac{y}{m}=x+c. When multiplying and dividing by something, every term on each side of the equals sign must be multiplied or divided by it.
- Expanding parentheses
When expanding parentheses, all terms within the parentheses must be multiplied by the value on the outside of the parentheses — in other words apply the distributive property. For example, 2(x+3), you get 2x+6 as both of the terms inside the bracket have been multiplied by 2.
- Not using the correct root to undo a power
When you have a variable raised to a power (exponent), you must use inverse operations (root) to remove that power. For example, if you have x^4 you need to calculate the 4 th root of the variable to get x. You cannot use the square root to undo the power of 4.
x^{4}\rightarrow inverse 4 th root \rightarrow\sqrt[4]{x^4}
Related math formulas lessons
- Math formulas
- Kinematic equations
Practice solving literal equation problems
1. Solve the equation x-2y=10 for y.




To solve the equation for y, means to isolate the y on one side of the equation. First, move the – \; 2y by doing the inverse operation which in this case is to add 2y.
\begin{aligned}x-2y+2y&=10+2y \\\\ x&=10+2y \end{aligned}
Next, move the 10 by doing the inverse operation, which is to subtract 10.
\begin{aligned}x-10&=10+2y-10 \\\\ x-10&=2y \end{aligned}
Finally divide throughout by 2 so that y is isolated.
\begin{aligned}\cfrac{x-10}{2}&=\cfrac{2y}{2} \\\\ \cfrac{x}{2}-5&=y \end{aligned}
OR
y=\cfrac{x}{2}-5
2. Rearrange the formula, A=s^2 so that s is isolated.




To solve the equation for s, do the inverse operation, which is to take the square root. Undoing a square is to take a square root.
Remember when taking the square root in solving equations, to include both the positive and negative solutions.
\begin{aligned}A&=s^2 \\\\ \sqrt{A}&=\sqrt{s^2} \\\\ \pm \; \sqrt{A}&=s \end{aligned}
OR
s=\pm \; \sqrt{A}
3. Solve the equation \cfrac{a}{b}+\cfrac{c}{d}=e, for c.




To solve the equation for c first move \cfrac{a}{b} by doing the inverse operation which in this case is to subtract.
\begin{aligned}\cfrac{a}{b}+\cfrac{c}{d}&=e \\\\ \cfrac{a}{b}-\cfrac{a}{b}+\cfrac{c}{d}&=e-\cfrac{a}{b} \\\\ \cfrac{c}{d}&=e-\cfrac{a}{b} \end{aligned}
Notice how the c is still not isolated. In order to isolate it, move the d by doing the inverse operation which is to multiply.
\begin{aligned}\cfrac{c}{d}&=e-\cfrac{a}{b} \\\\ d\cdot\cfrac{c}{d}&=d\cdot\left(e-\cfrac{a}{b}\right) \\\\ c&=d\left(e-\cfrac{a}{b}\right) \end{aligned}
4. The formula \cfrac{\theta\Pi{d}}{360}=A represents the arc length A of a sector of a circle with diameter d. Make d the subject of the formula.




To solve the formula, \cfrac{\theta\Pi{d}}{360}=A for d, first move 360 by doing the inverse operation which in this case is to multiply.
\begin{aligned}360\cdot\cfrac{\theta\Pi{d}}{360}&=A\cdot{360} \\\\ \theta\Pi{d}&=360A \end{aligned}
Notice how d is still not isolated on one side of the equation. Move the \theta and \Pi at the same time by doing the inverse operation which is division.
\begin{aligned}\theta\Pi{d}&=360A \\\\ \cfrac{\theta\Pi{d}}{\theta\Pi}&=\cfrac{360A}{\theta\Pi} \\\\ d&=\cfrac{360A}{\theta\Pi} \end{aligned}
5. Solve the equation for y.
m=\cfrac{y-x}{y}




To solve the equation, m=\cfrac{y-x}{y} for y, first move the y from the denominator by doing the inverse operation which is to multiply.
\begin{aligned}y\cdot{m}&=\cfrac{y-x}{y}\cdot{y} \\\\ ym&=y-x \end{aligned}
The y isn’t isolated and there are two terms that contain y. So, the next step is to move the y from the right to the left by doing the inverse operation which in this case is to subtract y.
ym-y=- \; x
In order to only have one y, factor out the y from the left side of the equation.
y(m-1)=- \; x
Now that there is one y, you can solve for it by moving the (m-1). To move it, do the inverse operation which is to divide.
\begin{aligned}\cfrac{y(m-1)}{(m-1)}&=\cfrac{- \; x}{(m-1)} \\\\ y&=\cfrac{- \; x}{m-1} \end{aligned}
6. Make b the subject of the formula \cfrac{a}{\sin(A)}=\cfrac{b}{\sin(B)}.




To solve the equation for b move \sin(B) by doing the inverse operation which in this case is to multiply.
\begin{aligned}\cfrac{a}{\sin(A)}&=\cfrac{b}{\sin(B)} \\\\ \sin(B)\cdot\cfrac{a}{\sin(A)}&=\cfrac{b}{\sin(B)}\cdot\sin(B) \\\\ \cfrac{\sin(B)a}{\sin(A)}&=b \end{aligned}
Literal equations FAQs
Yes, if the highest exponent in any equation is 2, it’s considered to be a quadratic equation. So, literal equations can be quadratic.
Yes, literal equations can contain an absolute value. The process to solve it would be the same as the steps taken when solving a regular algebraic absolute value equation.
In pre-algebra you are taught how to solve one-step, two-step, and multi-step equations. Your teacher might also expose you to some basic literal equations too.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!