Factoring - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Algebraic expressions Simplifying expressions Equivalent expressions Polynomials

Math resources Algebra

Factoring

Here you will learn strategies for factoring algebraic expressions, including quadratics and polynomials. Factoring is a vital tool when simplifying expressions and solving quadratic equations.

Students first learn how to factor in the $6$ th grade with their work in expressions and equations and expand that knowledge as they progress through algebra and beyond.

What is factoring?

Factoring is writing the algebraic expression as a product of its factors. It is the inverse process of multiplying algebraic expressions using the distributive property.

There are several strategies to factor algebraic expressions.

Step-by-step guide: Factoring out the GCF

Step-by-step guide: How to factor quadratic equations

Step-by-step guide: Factoring the difference of two squares

Step-by-step guide: Factor by grouping

What is factoring?

Common Core State Standards

How does this relate to $6$ th grade math – high school math?

Grade 6: Expressions and Equations (6.EE.A.3)
Apply the properties of operations to generate equivalent expressions. For example, apply the distributive property to the expression $3(2+x)$ to produce the equivalent expression $6+3x;$ apply the distributive property to the expression $24x+18y$ to produce the equivalent expression $6(4x+3y)$ .

Grade 7: Expressions and Equations (7.EE.A.1)
Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.

High School Algebra: Seeing Structure in Equations (HSA-SSE.B.3a)
Factor a quadratic expression to reveal the zeros of the function it defines.

[FREE] Algebra Worksheet (Grade 6 to 8)

Use this quiz to check your grade 6 – grade 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th to 8th grade algebra topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Algebra Worksheet (Grade 6 to 8)

DOWNLOAD FREE

How to factor algebraic expressions using the GCF

In order to factor out the $GCF$ from algebraic expressions:

Find the $\textbf{GCF}$ of all terms in the expression and place it in front of parentheses.
Divide each term in the expression by the $\textbf{GCF}.$
Put the divided terms in the parentheses.
Express the $\textbf{GCF}$ and the other factors as a product.

Factoring GCF examples

Example 1: factor the algebraic expression

4x-20

Find the $\textbf{GCF}$ of all terms in the expression and place it in front of parentheses.

The greatest common factor in the expression is $4.$

4(\ \ \ \ \ \ \ \ \ \ )

2Divide each term in the expression by the $\textbf{GCF}.$

Since $4$ is the $GCF,$

4x \div 4=x

-20 \div 4=-5

3Put the divided terms in the parentheses.

4(x-5)

4Express the $\textbf{GCF}$ and the other factors as a product.

4x-20=4(x-5)

Example 2: factor the algebraic expression

2x^{2}-4x

Find the $\textbf{GCF}$ of all terms in the expression and place it in front of parentheses.

The $GCF$ is $2x.$

$2x(\ \ \ \ \ \ \ \ \ \ )$

Divide each term in the expression by the $\textbf{GCF}.$

Since $2x$ is the $GCF,$

$2x^{2} \div {2x}=x$

$-4x \div {2x}=-2$

Put the divided terms in the parentheses.

2x( x-2 )

Express the $\textbf{GCF}$ and the other factors as a product.

2x^{2}-4x=2x(x-2)

How to factor algebraic expressions with a equal to 1

In order to factor an algebraic expression in the form $x^2+bx+c\text{:}$

Find two factors of the constant, $\textbf{c}$ term, that sum to equal the coefficient of the $\textbf{b}$ term.
Write the quadratic in factored form with two sets of parentheses.
Check your work and write the quadratic equation in factored form.

Example 3: factor the expression

x^{2}-3x-28

Find two factors of the constant, $\textbf{c}$ term, that sum to equal the coefficient of the $\textbf{b}$ term.

The constant, $c$ term, is $-28$ so one factor must be negative. The factors of $-28$ are:

$\begin{array}{rl}1,&-28 \\\\ -1,&28 \\\\ 2,&-14 \\\\ -2,&14 \\\\ 4,&-7 \\\\ -4,&7 \end{array}$

The coefficient of the $b$ term is $-3.$

The two factors that multiply to $-28$ and add to $-3$ are $-7$ and $4.$

$\begin{aligned}-7\cdot4&=-28 \\\\ -7+4&=-3 \end{aligned}$

Write the quadratic in factored form with two sets of parentheses.

The $a$ term breaks up to be $x\cdot{x}$ because $x\cdot{x}=x^{2}$

$x^{2}-3x-28=(x-7)(x+4)$

Check your work and write the quadratic equation in factored form.

You can check your work through distributive property.

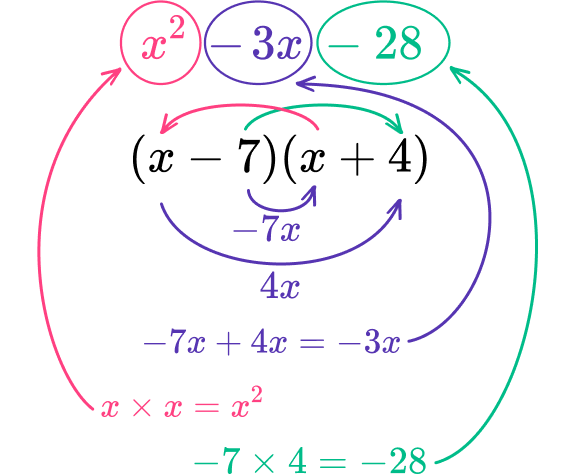
Example 4: factor the expression

x^{2}+7x+12

Find two factors of the constant, $\textbf{c}$ term, that sum to equal the coefficient of the $\textbf{b}$ term.

The constant, $c$ term, is $+ \; 12.$ As the $b$ term is also positive, both factors are positive. The factors of $12$ are:

$\begin{array}{rl}1,&12 \\\\ 2,&6 \\\\ 3,&4 \end{array}$

The coefficient of the $b$ term is $+ \; 7.$

The two factors that multiply to $+ \; 12$ and add to $7$ are $3$ and $4.$

$\begin{aligned} 3\cdot4&=12 \\\\ 3+4&=7 \end{aligned}$

Write the quadratic in factored form with two sets of parentheses.

The $a$ term breaks up to be $x\cdot{x}$ because $x\cdot{x}=x^{2}$

$x^{2}+7x+12=(x+3)(x+4)$

Check your work and write the quadratic equation in factored form.

You can check your work through distributive property.

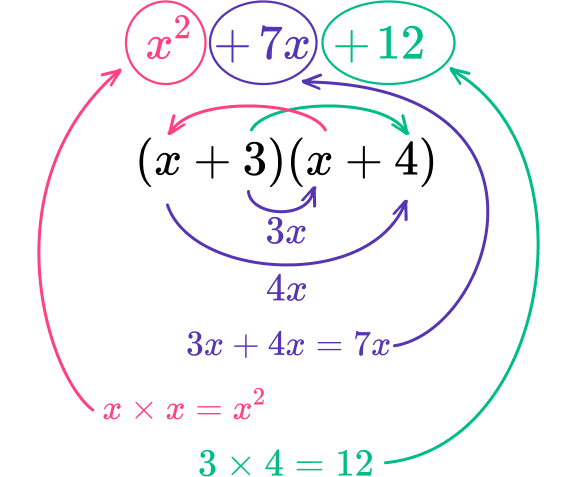
How to factor algebraic expressions with a not equal to 1

In order to factor an algebraic expression in the form $ax^{2}+bx+c\text{:}$

Find the factors of $\textbf{ac}$ that sum to equal the coefficient of the $\textbf{b}$ term.
Place the factors in the parentheses and check to make sure the product of the inside terms and outside terms sum to the $\textbf{b}$ term.
Write the quadratic equation in factored form.

Example 5: factor the expression

2x^{2}-11x+5

Find the factors of $\textbf{ac}$ that sum to equal the coefficient of the $\textbf{b}$ term.

The value of $ac$ is $2 \times 5=10.$ As the $b$ term is negative and the $c$ term is positive, both factors must be negative.

The factors of $10$ are:

$\begin{array}{cc}-1,&-10 \\\\ -2,&-5 \end{array}$

The coefficient of the $b$ term is $-11.$ The factors of $10$ that sum to $-11$ are $-1$ and $-10.$

Place the factors in the parentheses and check to make sure the product of the inside terms and outside terms sum to the $\textbf{b}$ term.

The $a$ term is $2x^{2}$ which you can factor into $2x$ and $x.$

So far, the factored quadratic looks like: $(2x\ \ \ \ \ )(x\ \ \ \ \ \ )$

As one of the parentheses contains $2x,$ the factor in the other bracket is multiplied by $2,$ therefore you must divide the factor by $2$ in the other bracket.

As $-10$ is a negative multiple of $2,$ you can easily divide this by $2$ to get $-5$ so you need to place the factor of $-1$ in the first pair of parentheses and $-5$ into the second pair of parentheses to get $(2x-1)(x-5).$

Now check the expansion.

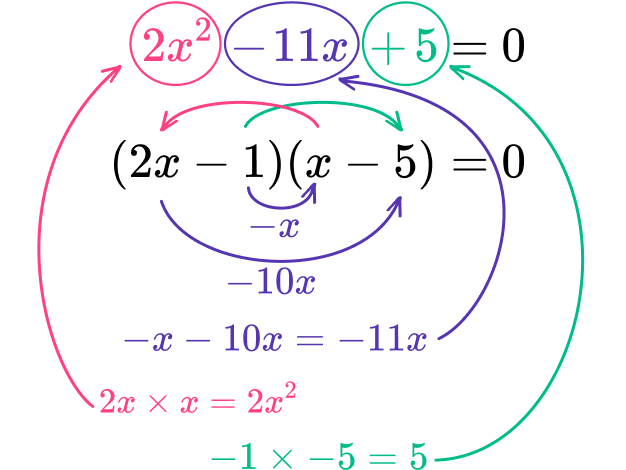
Each term is correct.

Write the quadratic equation in factored form.

2x^{2}-11x+5=(2x-1)(x-5)

Example 6: factor the expression

2x^{2}+5x+3

Find the factors of $\textbf{ac}$ that sum to equal the coefficient of the $\textbf{b}$ term.

The value of $ac$ is $2 \times 3=6.$ As the $b$ term is positive and the $c$ term is positive, both factors must be positive.

The factors of $6$ are:

$\begin{array}{cc}1,&6 \\\\ 2,&3 \end{array}$

The coefficient of the $b$ term is $+ \; 5.$ The factors of $6$ that sum to $5$ are $2$ and $3.$

Place the factors in the parentheses and check to make sure the product of the inside terms and outside terms sum to the $\textbf{b}$ term.

The $a$ term is $2x^{2}$ which you can factor into $2x$ and $x.$

So far, the factored quadratic looks like: $(2x\ \ \ \ \ )(x\ \ \ \ \ \ )$

As one of the parentheses contains $2x,$ the factor in the other bracket is multiplied by $2,$ therefore you must divide the factor by $2$ in the other bracket.

As $2$ is a multiple of $2,$ you can easily divide this by $2$ to get $1$ so you need to place the factor of $3$ in the first pair of parentheses and $1$ into the second pair of parentheses to get $(2x+3)(x+1).$

Now check the expansion.

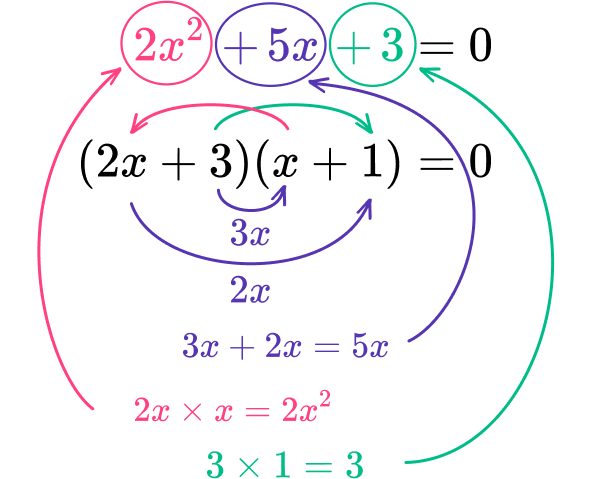
Each term is correct.

Write the quadratic equation in factored form.

2x^{2}+5x+3=(2x+3)(x+1)

How to factor algebraic expressions (difference of two squares)

In order to factor the difference of two squares.

Write two sets of parentheses.
Square root the first term and write it on the left hand side of both brackets
Square root the last term and write it on the right hand side of both brackets.

Example 7: factor the expression

4x^{2}-25

Write two sets of parentheses.

(\ \ \ \ \ \ )(\ \ \ \ \ \ )

Square root the first term and write it on the left hand side of both brackets.

The first term is $4x^{2}.$ Square root this to get

$\sqrt{4x^{2}}=2x$

$(2x\ \ \ \ \ \ )(2x\ \ \ \ \ \ )$

Square root the last term and write the two values on the right hand side of each bracket.

The last term is $25.$ Square root this to get

$\sqrt{25}=\pm5$

$(2x+5)(2x-5)$

How to factor algebraic expressions by grouping

In order to factor by grouping:

Group the first two terms together and the last two terms together.
Factor out the $\textbf{GCF}$ from each binomial.
Factor out the common binomial.

Example 8: factor the expression

2x^{3}-10x^{2}+3x-15

Group the first two terms together and the last two terms together.

(2x^{3}-10x^{2}) (3x-15)

Factor out the $\textbf{GCF}$ from each binomial.

2x^{2}(x-5)+3(x-5)

Factor out the common binomial.

(2x^{2}+3)(x-5)

Teaching tips for factoring

Use visual tools such as algebra tiles or digital algebra tiles so students can connect the area model with arrays to factoring.

Although worksheets have their place, having students work in collaborative groups to problem solve is essential to the math classroom.

Easy mistakes to make

Using the wrong factors
For example, factoring $x^{2}+5x+6,$ by using the incorrect factors of $6. \; (x+1)(x+6)$ ≠ ${x^{2}}+5x+6$ as $1+6=7,$ not $5.$ Here, the correct factored form is $(x+2)(x+3).$

Not factoring out the greatest common factor
For example, factoring $4x^{2}-16x$ to be $2(2x^{2}-8x). \; 2$ is not the $GCF$ of the expression, $4x$ is the $GCF.$ So, the correct factored expression is $4x(x-4).$

Not finding the square root when factoring the difference of squares
For example, factoring $16x^{2}-4$ to be $(8x-2)(8x+2).$ The correct factored expression should be $(4x-2)(4x+2)$ as $\sqrt{16x^{2}}=4x.$

Practice factoring questions

5(2-y)

10(1-y)

5(2-5y)

5(2+y)

The greatest common factor of $10$ and $5$ is $5.$ Divide both terms by $5$ to get $10-5y=5(2-y).$

4(5x^{2}-2x)

4x(5x-2)

2x(10x-4)

4x^{2}(5x-2)

The greatest common factor of $20x^{2}$ and $8x$ is $4x.$ Divide both terms by $4x$ to get $20x^{2}-8x=4x(5x-2).$

(x+2)(x-3)

(x-2)(x-3)

(x-2)(x+3)

(x+1)(x-6)

The factors of $-6$ that sum to $-1$ are $-3$ and $2.$

x^{2}-x-6=(x+2)(x-3)

(3x+5)(x-1)

(3x+5)(x+1)

(3x-5)(x-1)

(3x-5)(x+1)

For the quadratic, $3x^{2}-2x-5,$ the value of $ac$ is $3\times{-5}=-15.$ The factors of $-15$ that have a sum of $-2$ are $-5$ and $3.$ The $a$ term can be factored into $3x$ and $x$ so the factored form is currently $(3x\ \ \ \ \ )(x\ \ \ \ \ \ ).$

As one of the parentheses contains $3x,$ the factor in the other bracket is multiplied by $3,$ therefore divide the factor by $3$ in the other bracket.

As $3$ is a multiple of $3,$ you can easily divide this by $3$ to get $1$ so $-5$ is in the first pair of parentheses and $1$ is in the second pair to get $(3x-5)(x+1).$

(x+18)(x+18)

(x+3)(x-12)

(x+6)(x-6)

(x-3)(x-3)

The expression is the difference of two perfect squares. To factor this expression, take the square root of the first term and place it in the first position of each parenthesis.

x^{2}=36

\sqrt{x^{2}}=x

(x\ \ \ \ \ )(x\ \ \ \ \ )

Take the square root of the second term and place the values in the second position of each parenthesis.

\sqrt{36}=\pm6

(x+6)(x-6)

(x^{2}-4)(x-2)

(x^{2}+4)(x-2)

(x-4)(x^{2}-2)

(x+4)(x^{2}-2)

Group the first two terms and second two terms together.

(x^{3}-2x^{2}) (+4x-8)

The $GCF$ of the first set is $x^{2}$ and the $GCF$ of the second set is positive $4.$

x^{2}(x-2)+4(x-2)

Factor out the common binomial.

(x-2)(x^{2}+4)

Factoring FAQs

Can you factor expressions with more than one variable?

Yes, you can factor polynomial expressions with more than one variable. For example, $xy-3y,$ factors to be $y(x-3).$

Can you apply more than one strategy when factoring a polynomial expression?

Yes, sometimes when factoring expressions completely, you might have to apply more than one strategy. For example, when factoring $3x^{2}-27,$ you first factor out the $GCF.$ $3(x^{2}-9).$

Then you factor the parenthesis by using the strategy of the difference of two perfect squares. $\sqrt{x^{2}}=x$ and $\sqrt{9}=\pm3.$ So, the expression completely factored is $3(x-3)(x+3).$

Can you factor the difference of cubes?

Yes, there are strategies you will learn to factor the difference of cubes and the sum of cubes in Algebra $2.$

Can you factor the sum of two squares?

No, the sum of two squares is considered to be prime which means it cannot be factored. Quadratic polynomials can be prime meaning the only factors it has is itself and $1,$ like prime numbers.

Why is factoring algebraic expressions important?

Applying strategies of factoring helps to make solving equations easier. It can also help when finding the $x$ -intercepts of polynomial functions.

Can you factor expressions that have leading coefficients that are fractions or does the leading coefficient have to be an integer?

The leading coefficient of algebraic expressions can be fractions and they can be factored. For example, $\cfrac{1}{2}x-\cfrac{3}{4}$ factors to be $\cfrac{1}{2}\left(x-\cfrac{3}{2}\right).$

The next lessons are

Radicals
Radical functions
Vectors

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.