Explicit Formula

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Linear equations Substitution Arithmetic sequence Geometric sequence formula Recursive formula

Math resources Algebra Number patterns

Explicit formula

Here you will learn about explicit formulas, including what they are, how to use them and how to create them for arithmetic and geometric sequences.

Students will first learn about explicit formulas as part of algebra in high school.

What is an explicit formula?

The explicit formula of a sequence is a formula that enables you to find any term of a sequence.

Below are a few examples of different types of sequences and their $n$ th term formula.

Step by step guide: Quadratic sequences

See also: Cubic graph

On this page, you will look specifically at finding the $n$ th term for an arithmetic or geometric sequence.

What are arithmetic sequences?

An arithmetic sequence (arithmetic progression) is an ordered set of numbers that have a common difference between each consecutive term. The term-to-term rule tells how you get from one term to the next. In an arithmetic sequence, the rule will always be adding or subtracting a certain number.

Explicit formula

The $\textbf{n}$ th term of an arithmetic sequence is:

a_n=a_1+d(n-1)

Where,

$a_{n}$ is the nth term (general term)

$a_{1}$ is the first term

$n$ is the term position

$d$ is the common difference

For example,

6, 2, -2, -6, -10, ...

a_{1}=6

$d = -4$ (Each term is $4$ less than the one before it.)

So the explicit formula is $a_n=6+[-4(n-1)].$

What are geometric sequences?

A geometric sequence (geometric progression) is an ordered set of numbers where all terms but the first share a common ratio. The term-to-term rule explains how you get from one term to the next. In an arithmetic sequence the rule will always be multiplying by a certain number.

Explicit formula

The $\textbf{n}$ th term of a geometric sequence is:

a_{n}=a_{1}(r)^{n-1}

Where,

$a_{n}$ is the nth term (general term)

$a_{1}$ is the first term

$n$ is the term position

$n-1$ is the previous term and is an exponent

$r$ is the common ratio

For example,

1, 2, 4, 8, 16, 32, \dots

a_1=1

r=2

So the explicit formula is $a_n=1(2)^{n-1}$ or $a_n=2^{n-1}.$

What is an explicit formula?

Common Core State Standards

How does this relate to high school math?

Functions – Building Functions (HSF.BF.A.1)
Write a function that describes a relationship between two quantities.

Functions – Building Functions (HSF.BF.A.2)
Write arithmetic and geometric sequences both recursively and with an explicit formula, use them to model situations, and translate between the two forms.

Functions – Linear, Quadratic and Exponential Models (HSF.LE.A.2)
Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).

[FREE] Number Patterns Check for Understanding Quiz (Grade 4 to 5)

Use this quiz to check your grade 4 to 5 students’ understanding of number patterns. 10+ questions with answers covering a range of 4th and 5th grade number patterns topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Number Patterns Check for Understanding Quiz (Grade 4 to 5)

DOWNLOAD FREE

How to generate a sequence using an explicit formula

In order to generate a sequence using an explicit formula:

Find an explicit formula.
Substitute the given value into the formula to calculate the new value.
Repeat step $\bf{2}$ until the desired number of terms has been generated.

Explicit formula examples

Example 1: generating the terms of the arithmetic sequence

A sequence is defined by the explicit formula $a_n=a_1+2(n-1)$ and $a_1=3.$

Find the next four terms of the sequence.

Find an explicit formula.

The explicit formula is given in the question, $a_n=a_1+2(n-1)$ and $a_1=3.$

This creates the explicit formula $a_n=3+2(n-1).$

2Substitute the given value into the formula to calculate the new value.

a_2=3+2(2-1)=3+2(1)=5

3Repeat step $\bf{2}$ until the desired number of terms has been generated.

\begin{aligned}& a_3=3+2(3-1)=3+2(2)=7 \\\\ & a_4=3+2(4-1)=3+2(3)=9 \\\\ & a_5=3+2(5-1)=3+2(4)=11\end{aligned}

This first term is $3.$ The next four terms of the sequence are $5, 7, 9, 11.$

Example 2: generating a geometric sequence

A sequence is defined by the explicit formula $a_n=a_1(r)^{n-1}$ and $a_1=1$ and $r=4.$

Find the next four terms of the sequence.

Find an explicit formula.

The explicit formula is given in the question, $a_n=a_1(r)^{n-1}$ and $a_1=1$ and $r=4.$

This creates the explicit formula $a_n=1(4)^{n-1}$ or $a_n=4^{n-1}.$

Substitute the given value into the formula to calculate the new value.

a_2=4^{2-1}=4^1=4

Repeat step $\bf{2}$ until the desired number of terms has been generated.

\begin{aligned}& a_3=4^{3-1}=4^2=16 \\\\ & a_4=4^{4-1}=4^3=64 \\\\ & a_5=4^{5-1}=4^4=256 \end{aligned}

This first term is $1.$ The next four terms of the sequence are $4, 16, 64, 256.$

How to find the explicit formula of an arithmetic sequence

In order to find the explicit formula of an arithmetic sequence:

Identify the first term.
Find the common difference for the sequence.
Write the explicit formula in the form $\bf{\textbf{a}_\textbf{n}=\textbf{a}_1+\textbf{d}(\textbf{n}-1)}$ .

Example 3: finding the explicit formula for an increasing arithmetic sequence

Find the explicit formula for the sequence $5, 9, 13, 17, 21, \dots.$

Identify the first term.

The first term is $5.$

Find the common difference for the sequence.

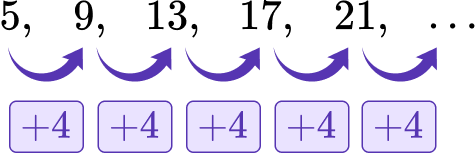
The common difference is $4.$

Write the explicit formula in the form $\bf{\textbf{a}_\textbf{n}=\textbf{a}_1+\textbf{d}(\textbf{n}-1)}$ .

The explicit formula of this sequence is $a_n=5+4(n-1).$

Note: You can simplify this to the equation $a_n=1+4 n.$

Example 4: find the explicit formula for a decreasing sequence, including negative numbers

Find the explicit formula for the sequence $3, 1, -1, -3, -5, \dots.$

Identify the first term.

The first term is $3.$

Find the common difference for the sequence.

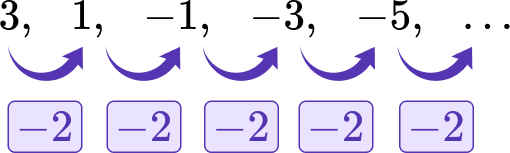
The common difference is $-2.$

Write the explicit formula in the form $\bf{\textbf{a}_\textbf{n}=\textbf{a}_1+\textbf{d}(\textbf{n}-1)}$ .

The explicit formula of this sequence is $a_n=3+[-2(n-1)].$

Note: You can simplify this to the equation $a_n=5-2 n.$

How to find the explicit formula of a geometric sequence

In order to find the explicit formula of a geometric sequence:

Identify the first term.
Find the common ratio for the sequence.
Write the explicit formula in the form $\bf{\textbf{a}_\textbf{n}=\textbf{a}_1(\textbf{r})^{\textbf{n}-1}}$ .

Example 5: finding the explicit formula for an increasing geometric sequence when a_₁ = 1

Find the explicit formula for the sequence $1, 3, 9, 27, 81, \dots.$

Identify the first term.

The first term is $1.$

Find the common ratio for the sequence.

Each term is $3$ times the one before it, so $r=3.$

Write the explicit formula in the form $\bf{\textbf{a}_\textbf{n}=\textbf{a}_1(\textbf{r})^{\textbf{n}-1}}$ .

The explicit formula of this sequence $a_n=1(3)^{n-1} \text { or } a_n=3^{n-1}.$

Example 6: finding the explicit formula for an increasing geometric sequence when a_₁ ≠ 1

Find the explicit formula for the sequence $4, 8, 16, 32, 64, \dots.$

Identify the first term.

The first term is $4.$

Find the common ratio for the sequence.

When the first term is not $1,$ you can solve for $r$ for any given term.

For example, substitute values for the second term…

$\begin{aligned}& a_n=a_1(r)^{n-1} \\\\ & 8=4(r)^{2-1} \\\\ & 8=4 r^1 \\\\ & 2=r\end{aligned}$

Write the explicit formula in the form $\bf{\textbf{a}_\textbf{n}=\textbf{a}_1(\textbf{r})^{\textbf{n}-1}}$ .

The explicit formula of this sequence $a_n=4(2)^{n-1}.$

Teaching tips for explicit formula

Give students time to explore the graph of each type of sequence in explicit form. Specifically have them use different values for $a_1$ and $d$ in arithmetic sequences, $a_n=a_1+d(n-1),$ and different values for $a_1$ and $r$ in geometric sequences, $a_n=a_1(r)^{n-1}.$

Look for worksheets that include both arithmetic and geometric sequences. This requires students to practice identifying the type of sequence and remembering which general explicit formula to use.

Easy mistakes to make

Confusing the recursive and explicit formulas for a sequence
The recursive formula shows how to find the next term based on the previous term. The explicit formula shows how to find any term based on the relationships between the term number and the term itself. It is easy to confuse the two.
For example,
$3, 6, 9, 12, 15, \dots$
The recursive formula is $a_{n+1}=a_n+3.$
The explicit formula is $a_n=3+3(n-1)$ or $a_n=3 n.$

Thinking the difference between $\bf{(\textbf{n}-1)}$ th and the nth term of the sequence is always positive
The common difference is only positive if the sequence of numbers is increasing. In a decreasing sequence, the common difference is negative.
For example,
$-2, \quad -4, \quad -6, \quad -8, \quad -10, …$
Since it is decreasing by $2$ each time, the explicit formula is $-2-2(n-1)$ not $-2+2(n-1)$ .

Confusing exponents and subscript
$a_4$ is not the same thing as $a^4.$ Always pay attention to where the number is. A smaller number written above (superscript) is an exponent. In this case, $a$ to the power of $4.$ A smaller number written below (subscript) is used to denote the number of the term number (or position of the term). In this case, the fourth term.

Thinking sequences always start at $\bf{\textbf{a}_1}$
While common, the first term of the sequence can be defined in other ways, such as $a_0.$ Always pay close attention to how the specific terms of $a$ are defined.

Incorrectly simplifying geometric sequences
In most cases, multiplying $a_1$ and $r$ will change the outcomes of the sequence.
For example,
The explicit formula of this sequence $a_n=4(2)^{n-1}$ is NOT the same as $a_n=8^{n-1}$ .

Number patterns
Shape patterns
Input/output tables
Quadratic sequence
Triangular numbers
Sequences

Explicit formula practice questions

4, 10, 16, 22

-8, -2, 4, 10

-12, -6, 0, 6

-12, -72, -432, -2,592

The formula is given in the question, $a_n=a_1+6(n-1)$ and $a_1=-2.$

This creates the explicit formula $a_n=-2+6(n-1).$

Substitute the given value into the formula to calculate the new value.

\begin{aligned}& a_2=-2+6(2-1)=-2+6(1)=4 \\\\ & a_3=-2+6(3-1)=-2+6(2)=10 \\\\ & a_4=-2+6(4-1)=-2+6(3)=16 \\\\ & a_5=-2+6(5-1)=-2+6(4)=22 \end{aligned}

12, 36, 108, 324

7, 11, 15, 19

7, 10, 13, 16

12, 48, 192, 768

The formula is given in the question, $a_n=a_1(r)^{n-1}$ where $a_1=3$ and $r=4.$

This creates the explicit formula $a_n=3(4)^{n-1}.$

Substitute the given value into the formula to calculate the new value.

\begin{aligned}& a_2=3(4)^{2-1}=3 \cdot 4^1=12 \\\\ & a_3=3(4)^{3-1}=3 \cdot 4^2=48 \\\\ & a_4=3(4)^{4-1}=3 \cdot 4^3=192 \\\\ & a_5=3(4)^{5-1}=3 \cdot 4^4=768\end{aligned}

a_n=0.3+0.2 n

a_n=0.2+0.3(n-1)

a_n=0.2+0.3 n

a_n=0.3+0.2(n-1)

The first term is $0.2,$ so $a_1=0.2.$

Find the common difference for the sequence.

US Webpages_ Explicit formula 5 US

The common difference is $0.3,$ so $d=0.3.$

Write the explicit formula in the form $a_n=a_1+d(n-1).$

The explicit formula of this sequence is $a_n=0.2+0.3(n-1).$

a_n=5(-1)^{n-1}

a_n=(-5)^{n-1}

a_n=-1(5)^{n-1}

a_n=-5(1)^{n-1}

The first term is $-1,$ so $a_1=-1.$

To find the common ratio for the sequence, use the general explicit formula to solve for $r$ for a given term.

\begin{aligned} a_n&=a_1(r)^{n-1} \\\\ -5&=-1(r)^{2-1} \\\\ -5&=-1 \cdot r \\\\ 5&=r\end{aligned}

Write the explicit formula in the form $a_n=a_1(r)^{n-1}.$

The explicit formula of this sequence $a_n=-1(5)^{n-1}.$

a_n=\cfrac{3}{8}+\cfrac{1}{4}(n-1)

a_n=\cfrac{3}{8}+\cfrac{1}{4} n

a_n=\frac{1}{4}+\frac{3}{8} n

a_n=\cfrac{1}{4}+\cfrac{3}{8}(n-1)

The first term is $\cfrac{1}{4},$ so $a_1=\cfrac{1}{4}.$

Find the common difference for the sequence.

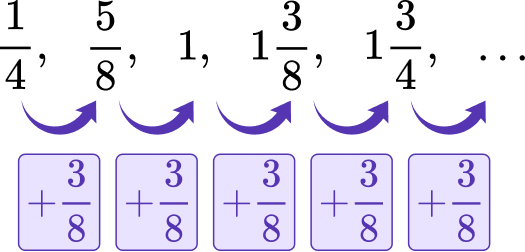
US Webpages_ Explicit formula 6 US

The common difference is $\cfrac{3}{8},$ so $d=\cfrac{3}{8}.$

Write the explicit formula in the form $a_n=a_1+d(n-1).$

The explicit formula of this sequence is $a_n=\cfrac{1}{4}+\cfrac{3}{8}(n-1).$

a_n=\cfrac{1}{2}(-2)^{n-1}

a_n=\cfrac{1}{2}(2)^{n-1}

a_n=(-1)^{n-1}

a_n=2\left(\cfrac{1}{2}\right)^{n-1}

The first term is $\cfrac{1}{2},$ so $a_1=\cfrac{1}{2}.$

To find the common ratio for the sequence, use the general explicit formula to solve for $r$ for a given term.

\begin{aligned} a_n&=a_1(r)^{n-1} \\\\ -1&=\cfrac{1}{2}(r)^{2-1} \\\\ -1&=\cfrac{1}{2} \cdot r \\\\ -2&=r\end{aligned}

Look what happens if you solve for an odd numbered term, instead of the second term.

\begin{aligned} a_3&=\cfrac{1}{2}(r)^{3-1} \\\\ 2&=\cfrac{1}{2} \cdot r^2 \\\\ 4&=r^2\end{aligned}

Since the square root of $4$ can be positive or negative, $r$ could be positive or negative. To decide, look at the terms in the sequence. Since they alternate between positive and negative, $r$ must be negative.

-4=r

Write the explicit formula in the form $a_n=a_1(r)^{n-1}.$

The explicit formula of this sequence is $a_n=\cfrac{1}{2}(-2)^{n-1}.$

Explicit formula FAQs

Does the first term have to be an integer?

No, the first term can be an integer, but it can also involve fractions or decimals or any real number.

What is the difference between a geometric sequence and a geometric series?

A geometric sequence is a sequence of numbers that has a common ratio. The sum of the terms in a geometric sequence is a geometric series.

The next lessons are

What is a function
Laws of exponents
Scientific notation

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.