Developing Critical Thinking Skills At KS2 Using Same Surface Different Depth Problems: How I Wish I’d Taught Maths (5)
Clare Sealy looks at the struggles primary school pupils can have when implementing critical thinking skills when subject knowledge is lacking, and the effect this can have on their attempts at problem solving activities in KS2.
This article is part of a series published to help primary school teachers and leaders implement some of the insights and teaching techniques derived from Craig Barton’s bestselling book How I Wish I’d Taught Maths. Links to the other 5 articles appear at the end.
In the introduction to this series, I outlined how Craig Barton, in his book How I wish I’d taught maths, described how he had changed his teaching as the result of reading research around learning and memory, in particular cognitive load theory in the classroom. In the latter part of his book, the focus turns to helping pupils use what they know.
Whatever the age of the children we teach, many find it hard to transfer what they know how to do in one context to another. This is most evident when it comes to maths problem solving, or in the SATs reasoning papers. They know the maths, they just can’t work out which bit of maths they need in this specific circumstance.
What are critical thinking skills?
At the basic level, critical thinking is the ability to analyse facts presented to us to form a judgement about a topic. It is an incredibly important skill to have at higher education and beyond, and is one of the key factors in astute decision making.
Most of us explicitly encounter critical thinking and other higher order thinking skills such as metacognition in the classroom at either GCSE or A-Level, but laying their foundations at primary school is becoming more and more common and valued.
However, “critical thinking and the ability to solve problems is not a generic skill that can be taught and that children can transfer from one problem to another. While there are some metacognitive strategies that can help a bit, what is really crucial is having a very secure understanding of the actual maths – the domain specific knowledge – that lies at the heart of the problem.” Daniel Willingham (2006)
Critical thinking (as well as scientific thinking and other domain-based types of thinking) is not a skill. There is not a set of critical thinking skills that can be acquired and deployed regardless of context. There are, however, metacognitive strategies that (once learned) make the critical thinking process more likely, and make up a key part of many quality first teaching methods.
The ability to think critically (to actually do what the metacognitive strategies call for) depends on domain knowledge and practice. For teachers, the situation is not hopeless, but no one should underestimate the difficulty of teaching pupils to think critically.
This said, metacognition is an incredibly valuable skill for pupils to have for any number of reasons, from helping low-ability students catch up to their peers to helping the whole class minimise the impact of the summer slide.
The metacognitive strategies mentioned involve reflecting on what you are doing during problem solving activities in KS2, asking yourself questions such as:
‘What am I doing?’
‘Why am I doing this?’
‘How does it help me?’
This is all very well if you have secure domain knowledge and can answer these questions. However, if you lack this knowledge, the questions are just frustrating.
Crib Sheet for How I Wish I'd Taught Primary Maths
Download the key findings from research; share with your staff, your SLT, and at your next job interview!
Download Free Now!How to help your pupils develop critical thinking skills for problem solving activities throughout KS2
There are of course problem solving strategies we can give pupils to help them become better critical thinkers. For example, underlining the important words. However, this relies on pupils understanding what the important word are in the first place.
Often, irrelevant surface features seem important to pupils whereas we experts can see they are completely irrelevant, because our domain knowledge and experience of answering many, many questions means we can spot the deep underlying structure a mile off.
It’s the same with other strategies such as setting work out systematically (you have to know what system is likely to be helpful), working backwards (you have to know whether this is likely to be useful in this situation) or even using a bar model. Bar models can be so helpful, but you have to know whether or not this kind of question is suitable for the bar model treatment.
‘Same surface, different deep’ or SSDD Problems
Problem solving maths questions usually have an arbitrary surface structure and a deep structure. The surface structure involves the context in which the problem is set and has nothing to do with the actual maths; for example, in a question about buying tickets to a funfair, the funfair and ticket are part of the surface structure.
They are but the wrapper in which the real maths is wrapped. Pupils can get fixated on this ‘wrapper’, rather than the underlying deep mathematical structure held within it.
I recall a SATs question about paving inside a greenhouse. The child thought that they couldn’t do it because they didn’t know what a greenhouse was! Whereas I immediately knew that this was going to be an area question. The surface structure was transparent to me whereas, it was thoroughly opaque to the pupil.
All the underlining, systematic working or bar modelling in the world wouldn’t get past this erroneous latching onto surface features.
How to get past the surface features
To overcome this hurdle, Craig recommends teaching children to recognise the deep structure of maths problems and how to identify and then disregard surface features.
It should go without saying that children need to be thoroughly secure in the underlying maths before attempting problem solving.

It is a mistake to think that maths problem solving is a good way of consolidating learning, let alone using it in the initial knowledge acquisition phase. Problem solving is about transferring learning from one context to another.
Problem solving at KS2 is about using your critical thinking skills to generalise
It therefore comes at the end of learning to do something, not mid- way and definitely not at the beginning.
But what is more, if at the end of a unit on, say division, we give children a load of division problems, this will not help them work out what the deep structure is. They already know; it’s division! This is fine, but it won’t help children learn to decide whether or not a particular problem requires division or not.
As well as problem solving activities at the end of units, teachers also need to allocate separate times where children have to work out what the deep structure of a problem actually is, regardless of surface features.
This means setting a range of SSDD problems sharing the same surface features – for example a shopping problem involving apples and pears – but which each have a different deep structure.
Read more: KS2 Problem Solving and KS3 Maths Problem Solving
Translating this to a primary school context
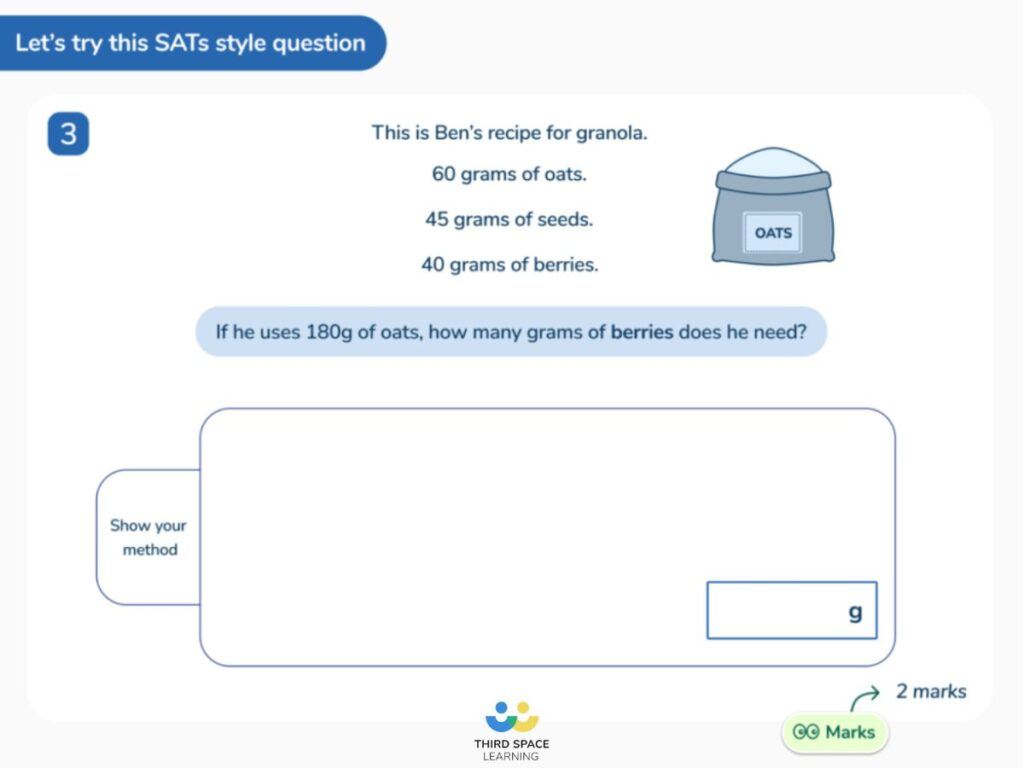
Let’s return to the question about stickers from the 2017 KS2 SATs paper we considered when considering goal free problems:

The surface feature here is stickers.
As experts, we know straightaway that we could substitute packs of stickers with boxes of apples or packets of balloons or even a family ticket to the cinema.
In fact, in a variation of Craig’s SSDD technique for a primary context, I’d suggest also doing DSSD problems (different surface, same deep) problems too, asking children to cross out the words ‘pack of stickers’ and replace with suitable alternative, and then repeat the problem to understand that the surface features do not change the underlying maths at all.

Then I’d suggest moving on to SSDD problems, with appropriate differentiation in the classroom. Let’s stick with stickers as our ‘same surface’.
The deep structure of our original question involved knowing that you had to multiply to find the price of 12 separate stickers and then subtracting to find the difference. But we could ask mathematically different questions while keeping the context and visual look of the problem the same.
For example:

- How much does one sticker cost? (though I’d adapt the price so the division came out as a whole number of pence)
- Stickers are 8cm wide and 6cm high. Ally sticks 3 stickers in a row, without any gaps. What is the perimeter of the shape she has now made?
- Ally buys 7 packs of stickers a month, Jack buys 3 packs of stickers a month and Chen buys 5 packets a month. What is the average number of packets bought by the 3 children in one month?
- Ally buys a pack of 12 stickers. She has spent 15% of her birthday money. How much birthday money has Ally got left? (again, I would adjust the price into something more workable)
Another great way to translate problem solving into a primary context is through topical maths investigations.
Extension ideas for problem solving activities in KS2
Extending both ideas, we could make a grid where the rows contained questions with a different surface structure and the columns contained questions with the same deep structure. This grid could be cut into individual boxes with pupils having to sort each box accordingly, to reconstruct the grid.

Tigers, Cake or Money? A unique approach to critical thinking
One questioning in the classroom strategy for helping children understand the deep structure of division problems, is to ask children if this is a tiger, cake or money sort of division question.
What this means is, could we swap the surface features of the problem we are given to one involving tigers, or cake or money?
Why these three I hear you ask?
This is because, where division problems do not divide exactly, it is really useful to:
- Be able to decide if you need to round up or down (These are the tiger questions. If you haven’t got enough cages for your tigers you might get eaten)
- Have a remainder that’s a fraction (These are the cake questions as we can each have 1 and a half cakes)
- Or have a remainder expressed as a decimal (These are the money questions as we can have £2.47 each)
An example of a Tiger question

This is a great example of a tiger question. With 4 spare tigers, you need to have an extra box! Having 2/3 of a box wouldn’t work, neither would having 0.666 of a box. Rewriting this as a tiger question helps understand the deep structure.
A cage holds 6 tigers
How many cages are needed to hold 52 tigers?
How to make a trickier Tiger question
Here is a slightly harder ‘tiger’ problem:
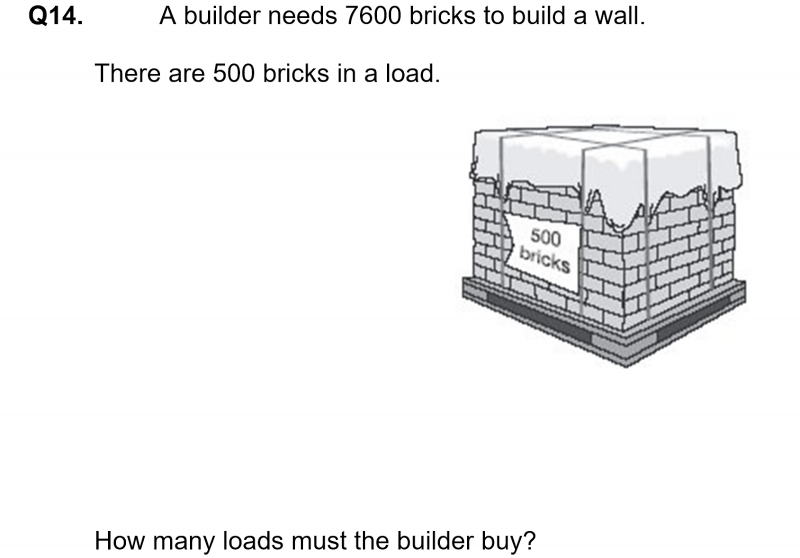
Let’s rewrite this:
A zookeeper has 7,600 tigers (!)
Cages can contain 500 tigers.
How many cages does the zookeeper need?
The answer:
15.2 cages is obviously not enough to stop the keeper from being eaten.
Answers requiring a decimal answer are usually money questions already, or calculations rather than word problems. Hence they are easy to categorise.
Some children find ‘tiger’ type questions particularly hard, and give answers that don’t make sense because they haven’t rounded up or down. So in the brick example above, they give the answer as 15.2 because they haven’t recognised that doesn’t make sense.
By naming certain deep structures, children are more able to identify them when they arise, and this is a fantastic way to help children with problem solving activities throughout KS2.
Sources of Inspiration
- Willingham, D.T. (2006) ‘How knowledge helps: it speeds and strengthens reading comprehension, learning and thinking’. American Educator 30 (1) p.30
This is the fifth blog in a series of 6 adapting the book How I Wish I’d Taught Maths for a primary audience. Some have already been mentioned in this post, but if you wish to read the remaining blogs in the series, check them out below:
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn how the programmes are aligned to maths mastery teaching or request a personalised quote for your school to speak to us about your school’s needs and how we can help.




