Standardised Scores In Education: What They Are, What They Mean, And How Best To Use Them
Standardised scores enable tests results across many primary schools or secondary schools to be compared against a national average and reviewed across different testing periods of time.
In this article experienced teacher and SATs veteran Sophie Bartlett explores standardised scores in depth so that you can better understand why schools and assessment organisations use them, what the best practice is for using and interpreting them and how they compare to other sorts of aggregated testing methodology such as scaled scores.
What are standardised scores?
A standardised score is the number of standard deviations a raw score is above or below the mean score. Students with raw scores above the mean have a positive standard score, whereas students with raw scores below the mean will have a negative standard score.
Standardised scores enable schools and the government to compare candidates’ test results to a national average.
The National Foundation for Educational Research (NFER), one of the largest assessment providers in the UK, defines standardised scores as:
“an example of a norm-referenced assessment. This is an assessment where pupils are assessed in comparison with the performance of other pupils. ‘Norm’ groups (e.g. the samples with which pupils are compared) are usually ones in which the scores have a normal distribution – they are distributed in a ‘normal’ or ‘bell-shaped’ curve.”
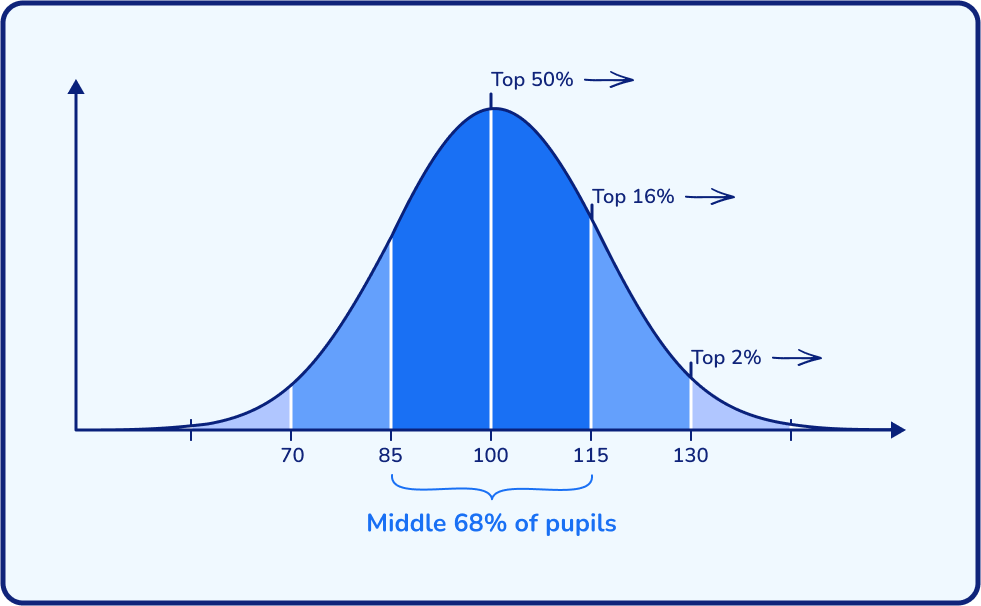
How do you calculate standardised scores?
Typically, older pupils achieve higher raw scores than younger pupils. Scores are optimised by age to add fairness for all pupils. This means pupils’ are compared with pupils in an appropriate nationally representative sample.
To calculate standardised scores, a large, nationally representative sample of candidates sit the test prior to publication. To calculate the standardised score of 100, exam boards usually take the average score (or the mean) raw score, regardless of difficulty.
The standard score indicates how many standard deviations a student’s raw score is above or below the mean score. Most standardised scores range from 70-140, with anything above 100 being above average, and below 100 being below average. Around ⅔ of scores will fall between 85 and 115.
For example, the mean raw score on a particular test is 65%, represented as a standardised score of 100. If a pupil scores 60% on this test, their standardised score might be around 95, depending on the standard deviation of the scores. Similarly, if they score 70%, their standardised score might be around 105. The exact standardised scores would depend on the distribution of the raw scores and the standard deviation used in the calculation.
The Ultimate Guide to Maths Mastery
All you need to know to successfully implement a mastery approach to mathematics in your primary school and help your pupils achieve a standardised score of at least 100.
Download Free Now!What are raw scores?
A raw score is the amount of marks a pupil earns on a test. They indicate the proportion of the total score achieved. These are given as a fraction (e.g. 8/10) or a percentage (e.g. 80%).
Although straightforward to understand and calculate, raw scores cannot compare performance across multiple tests. Raw scores don’t account for factors such as time, difficulty, age, or performance relative to others.
Standardised scores make the testing process more fair.
What are scaled scores?
A scaled score places all candidates onto a common scale, allowing comparisons across different versions of the test or between different groups of candidates. To calculate a scaled score, you must convert the raw score using a predetermined conversion table or formula from the test provider. This conversion adjusts for differences in difficulty between different versions of the test.
The government provided schools with the following information about the standard-setting process for the key stage 1 and key stage 2 national curriculum tests and understanding scaled scores:
”Tests are developed to the same specification each year. However, because the questions must be different, the difficulty of tests may vary. This means we need to convert the total number of marks a pupil gets in a test (their ‘raw’ score) into a scaled score, to ensure we can make accurate comparisons of performance over time.
Pupils scoring at least 100 will have met the expected standard on the test. However, given that the difficulty of the tests may vary each year, the number of raw score marks needed to achieve a scaled score of 100 may also change.
In 2016, panels of teachers set the raw score required to meet the expected standard. We have used data from trialling to maintain that standard for the tests from 2017 onwards.”
What is the difference between scaled scores and standardised scores?
A standardised score of 100 represents the average performance of a pupil in comparison to a nationally representative groups performance in the same test. Whereas, a scaled score of 100 is not the same as a standardised score of 100. Scaled scores of 100 is the expected standard to meet a tests difficulty level. This may change annually depending on assessment difficulty.
For example, here are the raw scores (out of 110) required to achieve a scaled score of 100 in the KS2 maths SATs:
| 2017 | 2018 | 2019 | 2022 | 2023 |
| 57 (52%) | 61 (55%) | 58 (53%) | 58 (53%) | 56 (51%) |
The scaled scores theory could conclude the easiest test was 2018’s KS2 maths test as it required the highest raw score for a scaled score of 100. Conversley, it appears the most difficult is the 2023 paper.
Scaled scores often have a defined range: in the KS1 SATs ranging from 85-115. In the KS2 SATs, scaled scores range from 80-120.
Why use standardised scores?
Schools in the UK often use standardised assessments, such as Rising Stars’ PiRA (Progress in Reading Assessment) and PUMA (Progress in Understanding Mathematics Assessment) tests, or the NFER tests.
In an independent trial with Rising Stars standardised tests, pupils receiving one to one maths support from Third Space Learning made 7 months’ progress in 14 weeks.
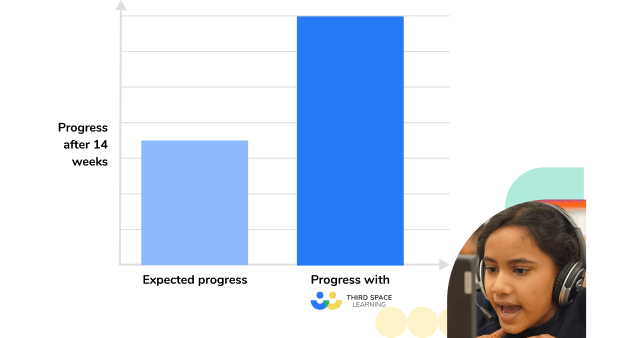
Being able to generate standardised scores is useful for comparing pupils against the national average, and for calculating their progress.
Standard deviation is key to turning raw test scores into standardised scores that are easy to compare and understand. It is a number that tells us how spread out the scores in a set of data are. If the standard deviation is low, the scores are close to the average score. If it’s high, the scores are more spread out.
In standardised scores, the standard deviation helps in a few ways:
- Compares scores: we can see how a particular score compares to the average score by measuring how many standard deviations it is above or below the average.
- Creates a common scale: many tests set the average score to 100 and use the standard deviation to show how far other scores are from this.
- Helps understand the spread of scores: knowing the standard deviation tells us if most scores are similar or if they vary a lot – a small standard deviation means most scores are close to the average and a large standard deviation means scores vary widely.
- To spot unusual scores: standard deviation helps identify scores that are much higher or lower than the average, therefore those that are unusually high or low.
How does the standardisation process work?
Steps involved in standardising scores
- Give the test to a large, nationally representative sample
- Calculate the raw scores
- Find the average (mean) score and how spread out the scores are (standard deviation)
- Change each raw score into a standardised score (with the mean raw score set at a standardised score of 100, and standard deviation defining the other scores)
- Adjust for age (if necessary)
Importance of representative samples in standardisation
A representative sample accurately reflects the diversity of the entire population. This ensures standardised scores are valid and reliable performance indicators across the whole group, without any bias towards a particular group.
Standardised scores derived from a representative sample can apply to the broader population. This allows educators and researchers to make meaningful comparisons and generalise findings to the entire population.
Representative samples help create consistent benchmarks, ensuring that standardised scores remain stable and comparable over time, even when administered to different groups. In addition, it allows for identifiying trends and patterns within the population.
Age-related expectations and their impact on scores
Age-related expectations identify the expectations of a pupil by a specified age or year group. Threshold descriptors define a set standard of expectation in the national curriculum. These indicate what a pupil should know by the end of key stage 2.
The Standards and Testing Agency (STA) scaled score of 100 on the year 2 and year 6 SATs represents the “expected standard” for the end of the relevant key stage.
Age-standardised scores, take pupils’ ages into account and compare a pupil’s standardised score with others of the same age (in years and months) in the nationally representative sample. A younger pupil might have a lower raw score than an older pupil but a higher standardised score. This is because the tests compare younger pupils to other younger pupils in the reference group, showing higher performance relative to their age group.
Interpreting standardised scores
In schools, standardised schools can be useful to see if a pupil is progressing appropriately. A number within a similar range each year (or perhaps more often, although mid-year tests aren’t always accurate as James Pembroke explores with further information) would demonstrate that a pupil is “on track”.
Since Ofsted’s interest in the ‘bottom 20%’ of pupils nationally, standardised scores have helped individual schools identify these pupils. James Pembroke explains that a standardised score of 87 puts a child into the 19th percentile, and therefore any pupil scoring 87 or below is worth prioritising for extra support.
Due to the limitations of standardised tests, a slight decrease in score does not always mean a lack of progress. Vice versa, a slight increase in score does not always equal accelerated progress. If the difference is significant – particularly a significant drop in score – this is worth taking note of. If a child needs extra support, these standardised scores are good evidence to provide for that.
Since 2013, Third Space Learning have provided one to one online maths tuition to pupils who need extra support most. Each expertly designed lesson aligns to the national curriculum. Therefore, pupils can catch up with the topics they need support with beyond whole class teaching.
Maths specialist tutors go through an extensive training programme to ensure they deliver the highest quality lessons to every pupil. This helps to accelerate their learning and understanding. Regular CPD ensures tutors use the latest teaching pedagogies, can ask questions based on pupil understanding and scaffold learning appropriately.
Standardised scores in education
Schools use standardised scores for two main reasons:
- To identify whether a pupil is above or below the national average
- To calculate progress by comparing scores from other standardised tests
NFER states that:
“all pupils scoring between 85 and 115 are demonstrating a broadly average performance. If the distribution is normal, this is expected to be around about two-thirds of the population.”
They also label the other score bands with the descriptions below:

Confidence bands, or confidence intervals, indicate the margin of error in standardised scores. They show how accurately the test measures a pupil’s performance. The margin of error is a statistical estimate based on the idea that tests only sample specific areas of learning. A pupil’s score might vary within a few points of their “true score.”
NFER tests calculate a “90% confidence band” to show this margin of error. This means you can be 90% sure that the true score lies within the confidence band.
“Rigorously developed tests, such as those published by NFER, provide confidence intervals or bands. These tell us the range in which a pupil’s ‘true score’ is (say, 90% of the time) likely to fall. To give one real-life example, on one year 4 reading test, a standardised score of 108 has a 90 percent confidence interval of -5/+4, meaning a nine-in-ten chance that the ‘true’ score is between 103 (i.e. 108-5) and 112 (i.e. 108+4).”
Limitations and criticisms of standardised scores
While standardised tests offer many benefits, they are not without their limitations.
1. Not aligned with a school’s curriculum
Often, they do not match a school’s curriculum. The tests expect students to know certain content, so if students haven’t learned that material yet, they’ll score poorly. This does not necessarily mean they aren’t capable.
2. Inconsistent administration
Standardised tests are not administered consistently like national assessments such as SATs and GCSEs. A school may not have strict policies on the administration of the tests. Different teachers within a school might handle the tests differently. Therefore, it may not be appropriate to compare test results administered under such varied conditions.
3. Outdated samples
With standardised scores, pupils’ results aren’t compared to others taking the test that year, but to pupils who took the test previously. An issue with this is the time difference between the test and when the initial sample test took place. National standards change over time, so tests need regular updates to stay accurate.
4. Correlation between scores and progress
Positive changes in standardised scores don’t always mean progress. If a test doesn’t match the learning in school, increasing scores might mean the test is more accurate, not that students are learning more. It is more likely that score changes matter if they are outside the usual range of variation. No change in score means the pupil stays in their national ranking, which is potentially a sign of progress.
Using standardised scores in education
Standardised scores are a useful educational tool, helping to compare pupil performance fairly. They allow teachers to track progress, identify the need for extra support or challenge and inform planning.
However, it’s important to remember they’re just one aspect of a pupil’s education. By using them alongside other measures, schools can ensure a more comprehensive understanding of each pupil’s abilities and needs.
Standardised Scores FAQs
Frequently asked questions
No FAQs available at the moment.
DO YOU HAVE PUPILS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the SATs revision programme or request a personalised quote for your school to speak to us about your school’s needs and how we can help.