Ratio scale

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

In order to access this I need to be confident with:

Arithmetic Scale maths Converting units of area and volume Adding and subtracting in standard form Multiplying and dividing in standard form Area How to calculate volume

This topic is relevant for:

GCSE Maths Ratio and Proportion Ratio

Ratio Scale

Here we will learn about a ratio scale, including using scale factors, scale diagrams and maps. We will also look at lengths, areas and volumes.

There are also ratio scale worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is ratio scale?

Ratio scale is a proportional relationship between two quantities. These quantities are usually length, area, and volume but can also include population, frequencies, temperature and money.

A model aircraft is created by taking the width of the real object and reducing the size of it using a scale factor. A scale factor is a number which is used to describe an enlargement.

We also have to consider the units for this example. Here, the original object is $15m$ wide, which is equal to $1500cm.$ The ratio of the model to the original (in centimetres) is $50:1500$ which simplifies to $1:30.$

So the ratio of the model to the real object would be $1:30$ as the real object is $30$ times larger than the model.

Top tip: The ratio scale is usually given in the form $1:n$ where $n$ is the scale factor of the enlargement ( $n$ can be positive or negative).

There are multiple topics that require a scale factor or a ratio scale to fulfil the specific criteria of the question.

What is ratio scale?

Maps

We can use a ratio scale to work out the actual distances represented on a map.

For example,

A map has a scale of $1:20 \ 000$ (read as $1$ to $20 \ 000$ ). This means that for every $1cm$ distance measured on the map, the real life value would be $20 \ 000$ times greater.

If we measure the distance between the Post Office and the Supermarket, we measure $4.2cm.$ The real / actual distance is therefore $4.2 \times 20 \ 000=84 \ 000 \ cm.$ To convert this to metres, we need to divide the distance by $100,$

$84 \ 000 \div 100=840m$ .

So the Supermarket is $840m$ away from the Post Office.

Length, area and volume

We can also use a ratio scale to compare the length, area and volume of shapes.

Let’s look at two similar 3D shapes.

Here we have two similar cuboids

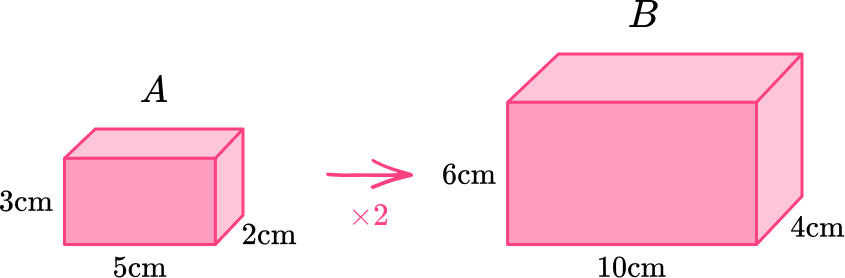
Ratio Scale Length, area and volume image 2

The lengths of cuboid $A$ have been multiplied by a scale factor of $2.$

We call this the length scale factor or $LSF$ . The ratio of the lengths of $A$ to $B$ is $1:2$ .

If we calculate the area of the front face rectangles we can find the area ratio.

Cuboid $A$ ’s front face has an area of $3 \times 5 = 15 \; cm^2$

Cuboid $B$ ’s front face has an area of $6 \times 10 = 60 \;cm^2$

The area of $A$ has been multiplied by a scale factor of $4$ to give the area of $B.$

We call this the area scale factor or $ASF$ . In general $ASF = LSF^2$

The ratio of the areas of $A$ to $B$ is $1:4$ .

If we calculate the volume of the cuboids we can find the volume ratio.

Cuboid $A$ has a volume of $3 \times 5 \times 2 = 30 \; cm^3$

Cuboid $B$ has a volume of $6 \times 10 \times 4 = 240 \; cm^2$

The volume of $A$ has been multiplied by a scale factor of $8$ to give the volume of $B.$

We call this the volume scale factor or $VSF$ . In general $VSF = LSF^3$

The ratio of the volumes of $A$ to $B$ is $1:8$ .

To summarise:

If we have any two similar shapes whose lengths are in the ratio $a:b$ .

Their areas will be in the ratio $a^2:b^2$ .

Their volumes will be in the ratio $a^3:b^3$ .

Bar modelling

Bar modelling can help for ratio scales because we can use the value of each share to determine a missing value. For example, below are a group of triangles arranged into a bar model.

If the total of the share value for $\text{B}$ was $24$ , what would the share value be for $\text{A}$ ?

Each triangle has the same share value and so if we know the share value of one triangle, we can calculate the total of the share values for $\text{A}$ .

$24 \div 2=12$ so each triangle is worth $12.$

Writing this onto the diagram, we get

Adding up the total value of the shares for $\text{A},$ we get $12+12+12=12 \times 3=36.$

Writing this as a ratio scale, we have used the ratio $3:2$ to find the other value in the ratio. This can be useful for reading map scales, finding missing lengths or drawing scale diagrams.

We could also find the total amount by adding up all the shares together. Here, this would be $12 \times 5=60.$

Step-by-step guide: Scale maths

How to use a ratio scale

In order to use a ratio scale:

Write down two related quantities from the question / diagram.
Calculate the scale factor / ratio of the two quantities.
Use the scale factor to determine other scaled values.

Explain how to use a ratio scale

Ratio scale worksheet

Get your free ratio scale worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Ratio scale worksheet

Get your free ratio scale worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on ratio

Ratio scale is part of our series of lessons to support revision on ratio. You may find it helpful to start with the main ratio lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Ratio scale examples

Example 1: similar shapes

Below are two similar shapes. Use the information provided to calculate the value of $x.$

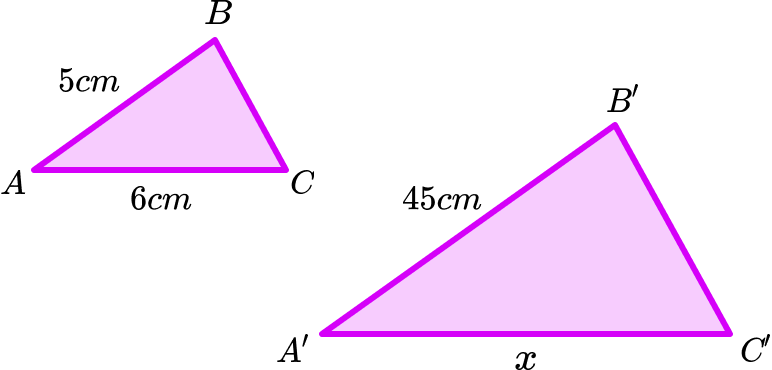
Write down two related quantities from the question / diagram.

We know the two lengths $\text{AB}$ and $\mathrm{A}^{\prime}\mathrm{B}^{\prime}$ and so we can write these as a ratio $5:45.$

2Calculate the scale factor / ratio of the two quantities.

Simplifying the ratio $5:45$ by dividing both sides by $5,$ we get the ratio $1:9.$

This means that the length of $\mathrm{A}^{\prime}\mathrm{C}^{\prime}$ is $9$ times greater than the length of $\text{AC}$ .

3Use the scale factor to determine other scaled values.

6 \times 9=54cm.

\mathrm{A}^{\prime}\mathrm{C}^{\prime}=54cm.

Example 2: reading a map scale

A map has a scale of $1:50 \ 000.$ The distance between two points on a map is equal to $5.6cm.$ Calculate the real distance in kilometres.

Write down two related quantities from the question / diagram.

As we have been given the ratio scale $1:50 \ 000$ , we can move on to step $3$ straight away.

Calculate the scale factor / ratio of the two quantities.

Move on to Step $3.$

Use the scale factor to determine other scaled values.

Using equivalent ratios, we can state the following

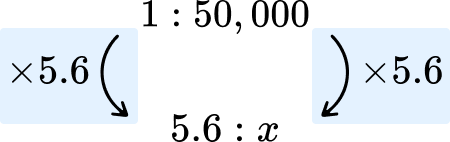
We therefore need to find the value of $x$ by calculating $50000 \times 5.6=280000.$

Converting $28000cm$ to $km,$ we get

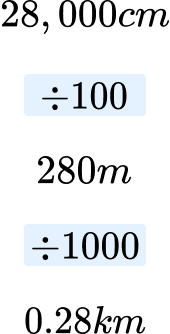
Example 3: scale model

A dinosaur bone measures $1.8m$ in length. Paula is producing a scale model of the dinosaur. A scale model of another bone measuring $0.96m$ in length, is $16cm$ long.

Calculate the length of the first bone for the model.

Write down two related quantities from the question / diagram.

The quantities we can use are the lengths of the second bone. The actual length is $0.96m \ (96cm)$ and the model length is $16cm.$

Calculate the scale factor / ratio of the two quantities.

This gives us the ratio $96:16$ which simplifies to $6:1.$ The model is $6$ times smaller than the original dinosaur bone.

Use the scale factor to determine other scaled values.

As the original bone is $1.8m \ (180cm)$ in length, the length of the scale model is equal to

$180 \div 6=30cm$ .

Example 4: standard form

The atomic radius of a magnesium atom is equal to $1.6 \times 10^{-8}cm.$ A centimetre is $10 \ 000 \ 000$ nanometres. Calculate the atomic radius of one atom of magnesium in nanometres.

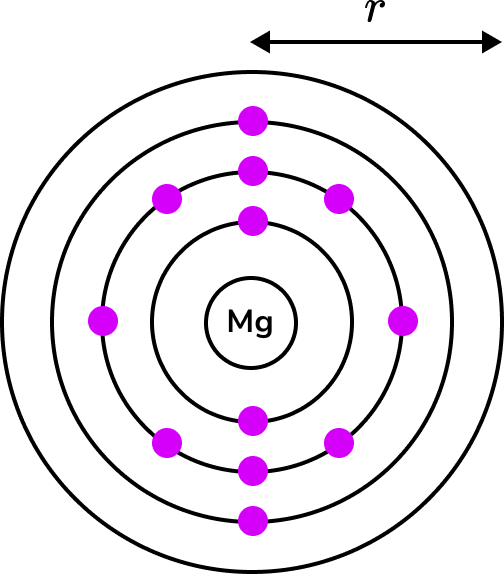
Write down two related quantities from the question / diagram.

Here we are converting units of length from centimetres to nanometres. It states that $1cm$ is equal to $10 \ 000 \ 000nm.$

Calculate the scale factor / ratio of the two quantities.

The ratio to convert centimetres to nanometres is therefore $1:10 \ 000 \ 000.$ In standard form, this is equal to $1:1 \times 10^{7}.$

Use the scale factor to determine other scaled values.

The atomic radius of magnesium is $1.6 \times 10^{-8}$ and so by multiplying this by $1 \times 10^{7}$ we get

$1.6 \times 10^{-8} \times 1 \times 10^{7}=1.6 \times 10^{-1}=0.16nm.$

The atomic radius of magnesium is $0.16nm.$

Example 5: area

Below are two similar rectangles. The area of rectangle $\text{A}$ is $12cm^{2}.$ The area of rectangle $\text{B}$ is $108cm^{2}.$ If the width of rectangle $\text{B}$ is $12cm,$ calculate the height of Rectangle $\text{A}$ .

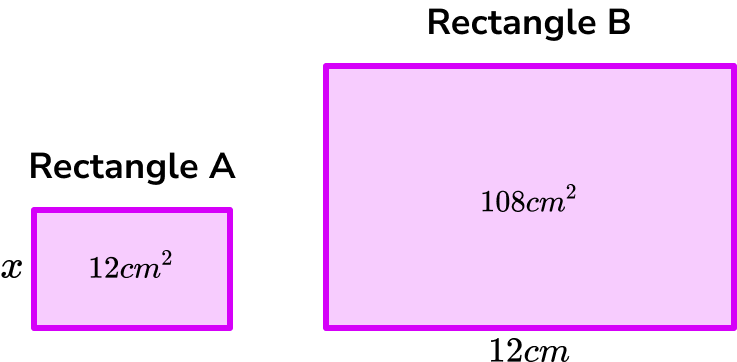
Write down two related quantities from the question / diagram.

The two quantities we can compare are the cross sectional areas for each cuboid, $12cm^2$ and $108cm^2.$

Calculate the scale factor / ratio of the two quantities.

12:108=1:9

As this is an area scale factor, we need to be careful with units. Here we have the ratio $1cm^{2}:9cm^{2}.$

To get the linear scale factor, we need to square root both parts of the ratio to get the length scale factor. $\sqrt{1}:\sqrt{9}=1:3$ so we now have the ratio $1:3$ for the lengths of the cuboid.

Use the scale factor to determine other scaled values.

As the width of Cuboid $\text{B}$ is $12cm, 108 \div 12=9cm,$ so the height of Cuboid $\text{B}$ is $9cm.$

We want to determine the value of $x$ in the ratio $x:9$ (the heights of the cuboids).

The equivalent ratio we can use is the ratio $1:3$ and so as $3 \times 3=9, 1 \times 3=x=3.$

The height of Cuboid $\text{A}$ is $3cm.$

Example 6: bar modelling

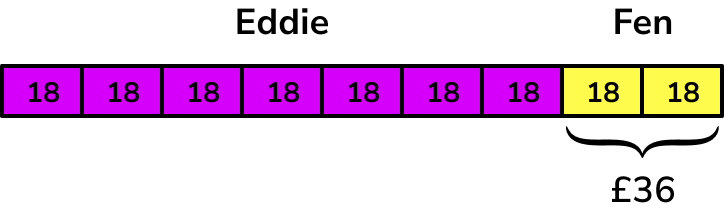
An amount of money is shared between Eddie and Fen in the ratio $7:2.$ If Fen received $£36,$ how much did Eddie receive?

Write down two related quantities from the question / diagram.

Using a bar model, we have

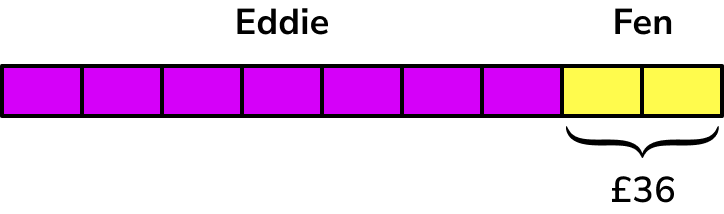
Calculate the scale factor / ratio of the two quantities.

As Fen’s $2$ parts are worth $£36$ we need to work out what one part is worth.

$36 \div 2=18$

Use the scale factor to determine other scaled values.

Eddie has $7$ parts, so receives $£126.$

$18 \times 7=£126$

Common misconceptions

Ratio scale used incorrectly

Make sure you have the ratio the correct way around. For example, the height of a scale drawing of a building is $0.32m.$ The actual height of the building is $96m.$

The ratio scale of the drawing to the real building is therefore $0.32:96 = 1:300$ so the real building is $300$ times taller than the drawing, not the other way around.

Converting units

The unit conversion is mixed up. For example, the ratio of the units of centimetres to millimetres is given as $10:1$ whereas this should be $1:10$ (there are $10mm$ in $1cm$ and so you must multiply $cm$ by $10$ to get $mm$ ).

Area and volume conversions

When given the area or volume of two shapes and you need to find a missing length, you need to determine the linear scale factor. This is done by finding the square root of the area scale factor or the cube root of the the volume scale factor respectively. For example, the two cuboids below are similar.

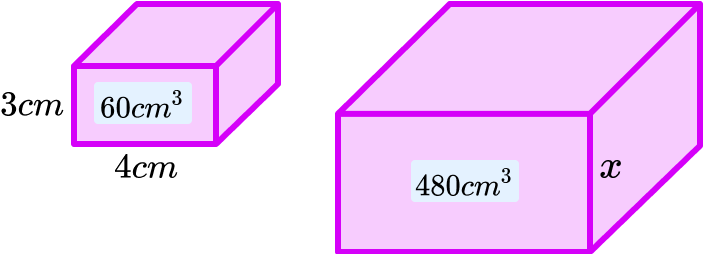
The volume scale factor would be equal to $60:480=1:8$ whereas the length scale factor would equal $\sqrt[3]{1}:\sqrt[3]{8}=1:2.$ This means that the volumes would be multiplied by $2^3$ whereas the lengths are multiplied by $2.$ Furthermore, the surface area would be multiplied by $2^{2}.$

Practice ratio scale questions

10cm

60cm

25cm

22.5cm

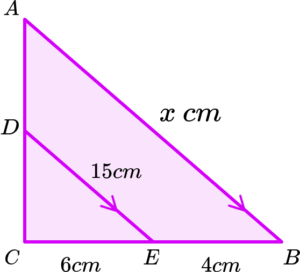
ratio scale practice question 1 explanation

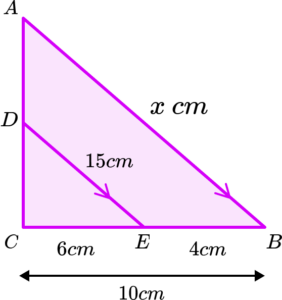
\begin{aligned} &CE:CB=6:10=1:\frac{5}{3} \\\\ &AB=15\times\frac{5}{3}=25\text{cm} \end{aligned}

50

80

500 \ 000

5

\begin{aligned} &25000cm=250m=0.25km \\\\ &20 \div 0.25=80cm \end{aligned}

12 \ 000

120

12

1 \ 200

\begin{aligned} &60 \times 200=12 \ 000cm \\\\ &12 \ 000 \div 100=120 m \end{aligned}

1:50000

1:5000

2:1

1:32000

\begin{aligned} &1µm=0.00001cm \\\\ &8µm=0.00008cm \\\\ &4 \div 0.00008=50000 \end{aligned}

9:16

16:9

3:4

4:3

Area

54:96=9:16

Length

\sqrt{9}:\sqrt{16}=3:4

77

7

42

84

\begin{aligned} &35 \div 5=7 \\\\ &6 \times 7=42 \\\\ &35+42=77 \end{aligned}

Ratio scale GCSE questions

1. Below is a scale drawing map of a desert island.

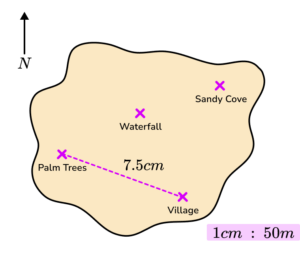
ratio scale gcse question 1

(a) Calculate the actual distance between the Palm Trees and the Village in centimetres.

(b) Gareth says “the distance between the Palm Trees and the Waterfall is $25m$ ”. Explain why Gareth must be wrong.

(3 marks)

Show answer

(a)

7.5 \times 50=375

(1)

37 \ 500 \ cm

(1)

(b)

The distance between the Palm Trees and the Waterfall is shorter than the distance between the Palm Trees and the Village.

$25m$ would only be $0.5 \ cm$ on the map, and the distance is longer than that

(1)

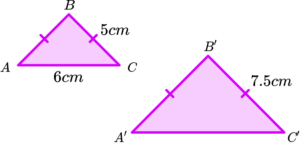
2. (a) Below are two similar isosceles triangles. Calculate the height of triangle $\mathrm{A}^{\prime}\mathrm{B}^{\prime}\mathrm{C}^{\prime}.$

ratio scale gcse question 2

(b) State the ratio of areas for triangles $\text{ABC}$ to $\mathrm{A}^{\prime}\mathrm{B}^{\prime}\mathrm{C}^{\prime}.$ Write your answer in its simplest form.

(6 marks)

Show answer

(a)

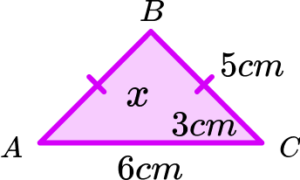
ratio scale gcse question 2 answer image 1

Pythagoras’ theorem: $x=\sqrt{5^{2}-3^{2}}=4\text{cm}$

(1)

5:7.5=1:1.5

(1)

4 \times 1.5=6cm

(1)

(b)

12:27

(1)

4:9

(1)

3. The table below shows an estimate for the distance a planet in the solar system is from Earth on one specific day.

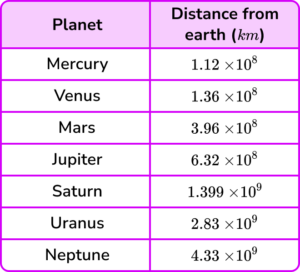
ratio scale gcse question 3

Calculate the ratio scale of the distances of Neptune from Earth, to Mercury from Earth? Write your answer in the form $1:n.$

(3 marks)

Show answer

(4.33 \times 10^{9}):(1.12 \times 10^{8})

(1)

(1.12 \times 10^{8}) \div (4.33 \times 10^{9})

(1)

1:2.5866 \times 10^{-2}

(1)

Learning checklist

You have now learned how to:

Use scale factors, scale diagrams and maps

Compare lengths, areas and volumes using ratio notation and/or scale factors – making links to similarity

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.