GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
Arithmetic Fractions, decimals and percentages Adding and subtracting fractions Multiplying and dividing fractions Adding and subtracting decimals Multiplying and dividing decimalsThis topic is relevant for:

Sample Space Diagram
Here we will learn how to use a sample space, including listing outcomes, creating sample space diagrams and finding probabilities.
There are also sample space worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is a sample space diagram?
A sample space diagram is used to display all possible outcomes, this could be as a list or a table of values. Making a list of all possible outcomes is known as enumeration.
To create a sample space diagram we need to think about the possible outcomes of a situation.
For example,
Let’s say we were to flip a fair coin and at the same time roll a fair six-sided die.
The sample space for this situation could be written as a list of the possible combinations.
(H, 1), \ (H, 2), \ (H, 3), \ (H, 4), \ (H, 5), \ (H, 6), \ (T, 1), \ (T, 2), \ (T, 3), \ (T, 4), \ (T, 5), \ (T, 6)The sample space for more complicated situations is often shown in a table.
For example,
If flipping the coin and rolling the die were part of a game and the side the coin shows changed the score of the die, we could show this in a sample space diagram.
In this game, the coin showing heads adds 1 to the value on the die. The coin showing tails doubles the value on the die.
The sample space diagram shows all the possible outcomes for this game.
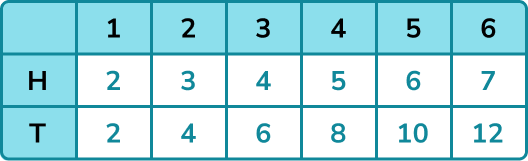
We can use sample space diagrams to find probabilities.
Jon plays the game and wants to know the probability of getting a score of more than 6.
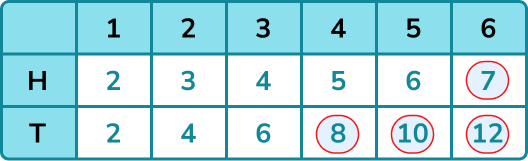
We can see from the table that there are 4 scores more than 6.
There are a total of 12 possible outcomes from this game.
Using the theoretical probability formula,
\text{P(score more than 6)}=\frac{4}{12}=\frac{1}{3}.The tables used for sample space diagrams can also be referred to as two-way tables.
Step-by-step guide: Two-way tables (coming soon)
What is a sample space?

How to use a sample space diagram
In order to find a probability using a sample space diagram:
- Use information provided to decide whether to write a list or create a table to find all possible outcomes.
- Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
- Use the information from the list or table to find any probabilities required.
Explain how to use a sample space

Sample space worksheet

Get your free sample space worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Sample space worksheet

Get your free sample space worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on combined events
Sample space diagram is part of our series of lessons to support revision on combined events. You may find it helpful to start with the main combined events lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Sample space diagram examples
Example 1: writing a list of possible outcomes
A fair coin is flipped and a 4 sided spinner numbered 1 to 4 is spun.
Write a list of all possible combinations of outcomes and find the probability of getting a tail and an even number.
- Use information provided to decide whether to write a list or create a table to find all possible outcomes.
This question requires a list of outcomes. The coin has two outcomes – H and T, the spinner has 4 outcomes, 1, 2, 3 and 4. We can write them as pairs e.g. (H, 1).
We should have 4 options for each side of the coin, so 8 outcomes in total. It is best to list them in a systematic way to ensure we don’t miss any combinations.
2Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
(H, 1), \ (H, 2), \ (H, 3), \ (H, 4), \ (T, 1), \ (T, 2), \ (T, 3), \ (T, 4).3Use the information from the list or table to find any probabilities required.
There are two possible outcomes that have a Tail and an even number.
(H, 1), \ (H, 2), \ (H, 3), \ (H, 4), \ (T, 1), \ \colorbox{yellow}{(T, 2),} \ (T, 3), \ \colorbox{yellow}{(T, 4).} \text{P(tail and even number)}=\frac{2}{8}=\frac{1}{4}.Example 2: creating a sample space table
Two fair spinners, one numbered 1, 2 and 3, the other 2, 5, and 7 are spun.

The scores on the spinners are added together. Find the probability that the total score is a prime number.
Use information provided to decide whether to write a list or create a table to find all possible outcomes.
The easiest way to organise the outcomes here is a table.
The spinners each have 3 outcomes so we should have 9 possible outcomes in total.
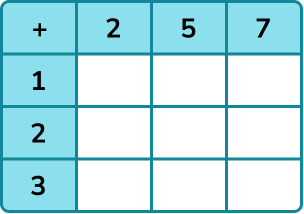
Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
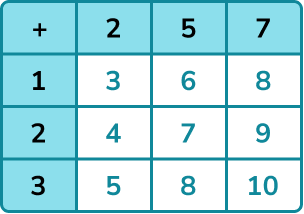
Use the information from the list or table to find any probabilities required.
There are three possible outcomes that are prime.
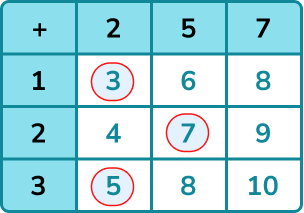
\text{P(Total score is prime)}=\frac{3}{9}=\frac{1}{3}
Example 3: creating a sample space diagram using a rule
A fair coin is flipped and a fair six-sided die is rolled. If the coin shows heads, the score on the die is increased by 3. If the coin shows tails the score on the die is decreased by 1. Find the probability of getting a score less than 5.
Use information proved to decide whether to write a list or create a table to find all possible outcomes.
This question is best answered with a table. The coin has 2 outcomes and the die has 6 outcomes so we should have 12 possible outcomes in total.
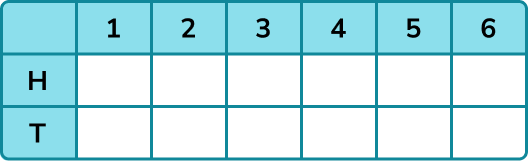
Systematically write the list or fill in the table by either listing outcomes or performing operations with values.
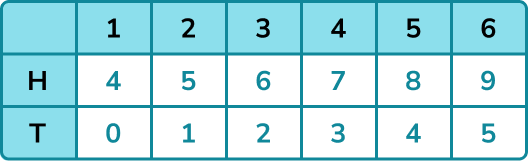
Use the information from the list or table to find any probabilities required.
There are six possible outcomes that are less than 5.
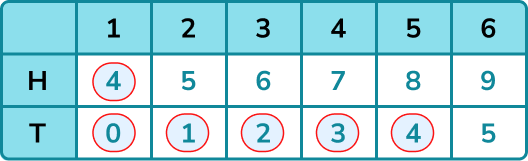
\text{P(Score less than 5)} = \frac{6}{12} = \frac{1}{2}.
Common misconceptions
- Missing out or repeating outcomes when listing
A common error is to miss out some outcomes or repeat one already listed. This can happen if we do not use a systematic approach to forming the list.
Creating a table to list the outcomes can help structure our list to ensure none are missed or repeated.
Practice sample space diagram questions
1. A fair coin is flipped and a 5 sided spinner is spun. How many possible outcomes are there?




The coin has 2 outcomes and the spinner has 5 outcomes. The total number of outcomes is 2 \times 5 =10 .
2. A fair coin is flipped and a 4 sided spinner numbered 1 to 4 is spun. If the coin shows heads the score on the spinner is doubled. If the coin shows tails the score on the spinner is tripled. Draw a sample space diagram for this situation.

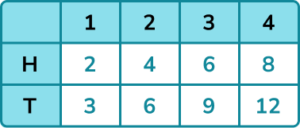

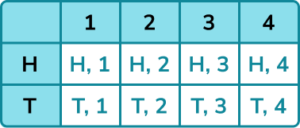

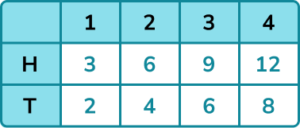

A table is more suitable because we are applying an operation to each score on the spinner.
3. The sample space diagram shows the possible outcomes when two normal fair dice are rolled and the difference between values is calculated.
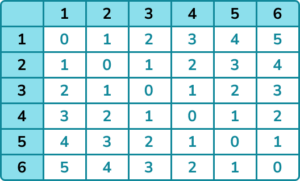
Use the sample space diagram to find the probability of getting a difference of 2 or less.




There are 24 outcomes that are 2 or less out of a total of 36.
\frac{24}{36} = \frac{2}{3}
4. A fair coin is flipped and a 4 sided spinner numbered 1 to 4 is spun. If the coin shows heads, the score on the spinner is doubled. If the coin shows tails the score on the spinner is tripled. Find the probability of getting an even score.




There are 6 even outcomes out of 8 outcomes in total.
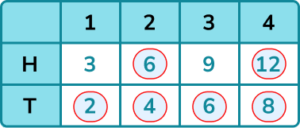
5. Three fair coins are flipped together. Each coin has either a head or a tail. Find the probability of getting 2 heads and one tail.




There are 3 outcomes which have 2 heads and 1 tail, out of 8 outcomes in total.
![]()
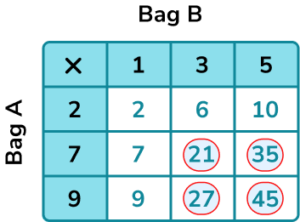
6. Two bags each contain 3 numbered counters. Bag A contains the numbers 2, 7 and 9. Bag B contains the numbers 1, 3 and 5.
A counter from each bag is selected at random and their values multiplied together. Find the probability of getting a result greater than 10.




There are 4 outcomes greater than 10, out of 9 outcomes in total.
Sample space diagram GCSE questions
1. Two fair 6 sided dice are rolled and the product of the values is recorded.
(a) Complete the sample space diagram to show the possible outcomes.

(b) Find the probability of getting a product less than 12.
(4 marks)
(a)
Evidence that the product of the values is found.
(1)
Table complete with no more than one error.
(1)
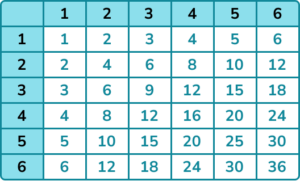
(b)
Fraction out of 36 given.
(1)
\frac{19}{36}(1)
2. A 4 sided spinner numbered 1, 2, 3 and 4 and a 3 sided spinner numbered 5, 7 and 9 are spun and the values on each added together.
(a) Complete the sample space diagram to show the possible outcomes.
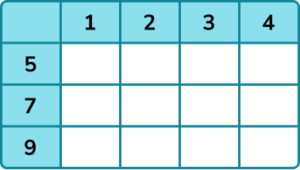
(b) Find the probability that the sum of the values is prime.
(4 marks)
(a)
Evidence that the sum of the values is found.
(1)
Table complete with no more than one error.
(1)
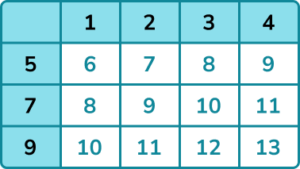
(b)
Fraction out of 12 given.
(1)
\frac{4}{12} or equivalent.
(1)
3. A combination lock has three dials each numbered 1, 2 and 3.

John has forgotten his combination but he remembers that exactly two of the numbers are the same.
(a) Write a list of the possible combinations.
(b) Find the probability of the combination numbers having a sum of 5.
(5 marks)
(a)
Evidence of of combinations with 1,1,.. 2,2,.. 3,3,..
(1)
At least 12 different combinations.
(1)
All 18 combinations.
(1)
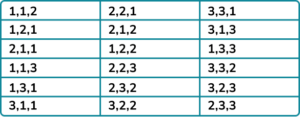
(b)
A fraction with a denominator of 18 .
(1)
\frac{6}{18} or equivalent.
(1)
Learning checklist
You have now learned how to:
- Generate theoretical sample spaces for single and combined events with equally likely, mutually exclusive outcomes and use these to calculate theoretical probabilities
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.